catalogue

Prefix expression

Infix expression

Suffix expression (inverse Polish)

Inverse Polish calculator

code implementation

Infix to suffix expression

Prefix expression

Prefix expression is also called polish. The operator of prefix expression is before the operand.

For example: (3 + 4) * 5-6 corresponding prefix expression is - * + 3 4 5 6

Scan the expression from right to left. When encountering a number, push the number into the stack. When encountering an operator, pop up two numbers at the top of the stack, use the operator to perform corresponding operations on them, and put the result into the stack; Repeat the above process to the leftmost end of the expression, and the value of the final operation result is the expression result.

For example: (3 + 4) × The prefix expression corresponding to 5-6 is - * + 3 4 5 6. The evaluation steps for the prefix expression are as follows:

1. Scan from right to left and press 6 5 4 3 into the stack;
2. Encounter the + operator, so pop up 3 ￠ and 4 (3 ￠ is the top element of the stack and 4 ￠ is the secondary top element), calculate the value of 3 + 4, get 7, and then put 7 on the stack;
3. Put 5 into the stack;
4. Next is × Operator, so pop up 7 and 5 to calculate 7 × 5 = 35, put 35 into the stack;
5. Finally, the - Operator calculates the value of 35-6, i.e. 29, so as to obtain the final result

Infix expression

Infix expression is a common operation expression, such as (3 + 4) * 5-6

The evaluation of infix expression is the most familiar to us, but it is not easy to operate for computers. Therefore, infix expression is often converted to suffix expression in calculation

Suffix expression (inverse Polish)

Suffix expression, also known as inverse Polish expression, is similar to prefix expression, except that the operator is after the operand.

Scan the expression from left to right. When encountering a number, push the number into the stack. When encountering an operator, pop up two numbers at the top of the stack, use the operator to perform corresponding operations on them, and put the result into the stack; Repeat the above process to the rightmost end of the expression, and the value of the final operation result is the expression result.

For example: (3 + 4) × The suffix expression corresponding to 5-6 is 3, 4 + 5 × 6 -, evaluate the suffix expression as follows:

1. Scan from left to right and press 3 and 4 into the stack;
2. Encounter the + operator, so pop up 4 and 3 (4 is the top element of the stack and 3 is the secondary top element), calculate the value of 3 + 4, get 7, and then put 7 on the stack;
3. Put 5 into the stack;
4. Next is × Operator, so pop up 5 and 7 and calculate 7 × 5 = 35, put 35 into the stack;
5. Put 6 into the stack;
6. Finally, the - Operator calculates the value of 35-6, i.e. 29, so as to obtain the final result

Inverse Polish calculator

1. Enter an inverse Polish expression (suffix expression), use stack, and calculate the result
2. It supports parentheses and multi digit integers, because here we mainly talk about data structures, so the calculator is simplified and only supports the calculation of integers.

code implementation

public class PolandNotation {

	public static void main(String[] args) {
		// Define inverse Polish expression
		// (3+4) × The suffix expression corresponding to 5-6 is 3 4 + 5 * 6-
		// Numbers and symbols are separated by spaces for convenience
		String suffixExpression = "3 4 + 5 * 6 - ";// 29

		// thinking
		// 1. First put "3 4 + 5 * 6 -" into ArrayList
		// 2. Pass the ArrayList to a method to cooperate with the stack to complete the operation

		List<String> List = getListString(suffixExpression);
		System.out.println("rpnList=" + List);

		int res = calculate(List);
		System.out.println("The result of the calculation is=" + res);
	}

	// Put the inverse Polish expression, data and operators into ArrayList in turn to facilitate scanning
	public static List<String> getListString(String suffixExpression) {
		// Split suffixExpression
		String[] split = suffixExpression.split(" ");
		List<String> list = new ArrayList<String>();
		for (String ele : split) {
			list.add(ele);
		}
		return list;
	}

	// Complete the inverse Polish expression operation, and the scanning expression becomes a traversal of the list
	public static int calculate(List<String> ls) {
		// To create a stack, only one stack is required
		Stack<String> stack = new Stack<String>();
		// Traversal ls
		for (String item : ls) {
			// Fetch number with regular expression
			if (item.matches("\\d+")) {// The number of multiple bits matches
				// Push 
				stack.push(item);
			} else {
				// pop out two numbers, operate them, and then put them on the stack
				int num2 = Integer.parseInt(stack.pop());
				int num1 = Integer.parseInt(stack.pop());
				int res = 0;
				if (item.equals("+")) {
					res = num1 + num2;
				} else if (item.equals("-")) {
					res = num1 - num2;
				} else if (item.equals("*")) {
					res = num1 * num2;
				} else if (item.equals("/")) {
					res = num1 / num2;
				} else {
					throw new RuntimeException("Incorrect operator");
				}
				// Put res on the stack
				stack.push("" + res);// Integer to string
			}
		} // for
			// The last thing left in the stack is the operation structure
		return Integer.parseInt(stack.pop());
	}

}

Infix to suffix expression

As you can see, the suffix expression is suitable for calculation, but it is not easy for people to write it, especially when the expression is very long. Therefore, in the development, we need to convert the infix expression into the suffix expression.

step

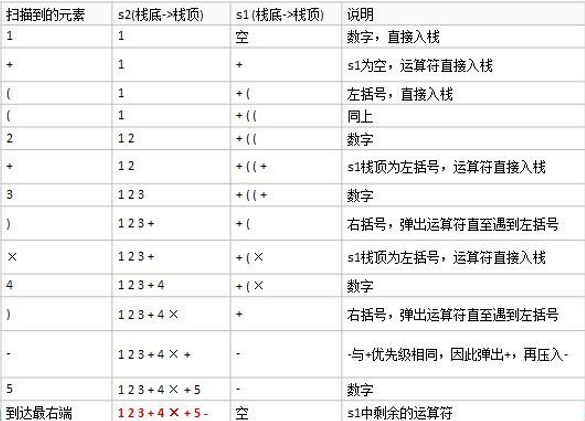
1. Initialize two stacks: operator stack s1 and stack s2 for storing intermediate results;
2. Scan infix expression from left to right;
3. When encountering an operand, press it to s2;
4. When an operator is encountered, compare its priority with s1 stack top operator:
   1. If s1 is empty, or the stack top operator is an open bracket "("), this operator is directly put on the stack;
   2. Otherwise, if the priority is higher than that of the operator at the top of the stack, the operator is also pressed into s1;
   3. Otherwise, pop up the operator at the top of s1 stack and press it into s2, go to (4.1) again and compare it with the new operator at the top of s1 stack;
5. When parentheses are encountered:
   1. If it is an open bracket "(", press s1 directly
   2. If it is the closing parenthesis ")", the operators at the top of s1 stack will pop up in turn and press s2 until the left parenthesis is encountered. At this time, this pair of parentheses will be discarded
6. Repeat steps 2 through 5 until the rightmost part of the expression
7. Pop up the remaining operators in s1 and press them into s2
8. Pop up the elements in s2 in turn and output them. The reverse order of the result is the suffix expression corresponding to the infix expression

give an example

Infix expression "1 + ((2 + 3) × 4) - 5 "converted to suffix expression" 1 2 3 + 4 " × + 5 –"