1, Multiple linear regression

In regression analysis, if there are two or more independent variables, it is called multiple regression. In fact, a phenomenon is often associated with multiple factors. It is more effective and practical to predict or estimate the dependent variable by the optimal combination of multiple independent variables than to predict or estimate only one independent variable. Therefore, multivariate linear regression is more practical than univariate linear regression.

Problem overview:
The trend of market house price is affected by many factors. Through the analysis of many factors affecting market house price, it is helpful to make a more accurate evaluation of the trend of house price in the future.
Multiple linear regression is suitable for the analysis of data affected by multiple factors. It is more effective and practical to predict or estimate dependent variables by the optimal combination of multiple independent variables. Based on the mathematical model, this paper arranges the relevant data such as house sales price in a certain area in the past, analyzes the data by using the method of multiple linear regression, and forecasts the future house price trend in this area.

2, Data cleaning

(1) Numerical data processing

1. Main problems of data set

Missing data
Inconsistent data
There is "dirty" data
Nonstandard data

The data set mainly has the following problems: data is missing, and some data is equal to 0

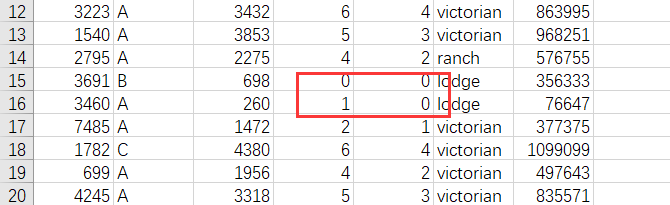
2. Delete duplicate data
First select the data to be processed, and then select data - Data Tool - delete duplicate values

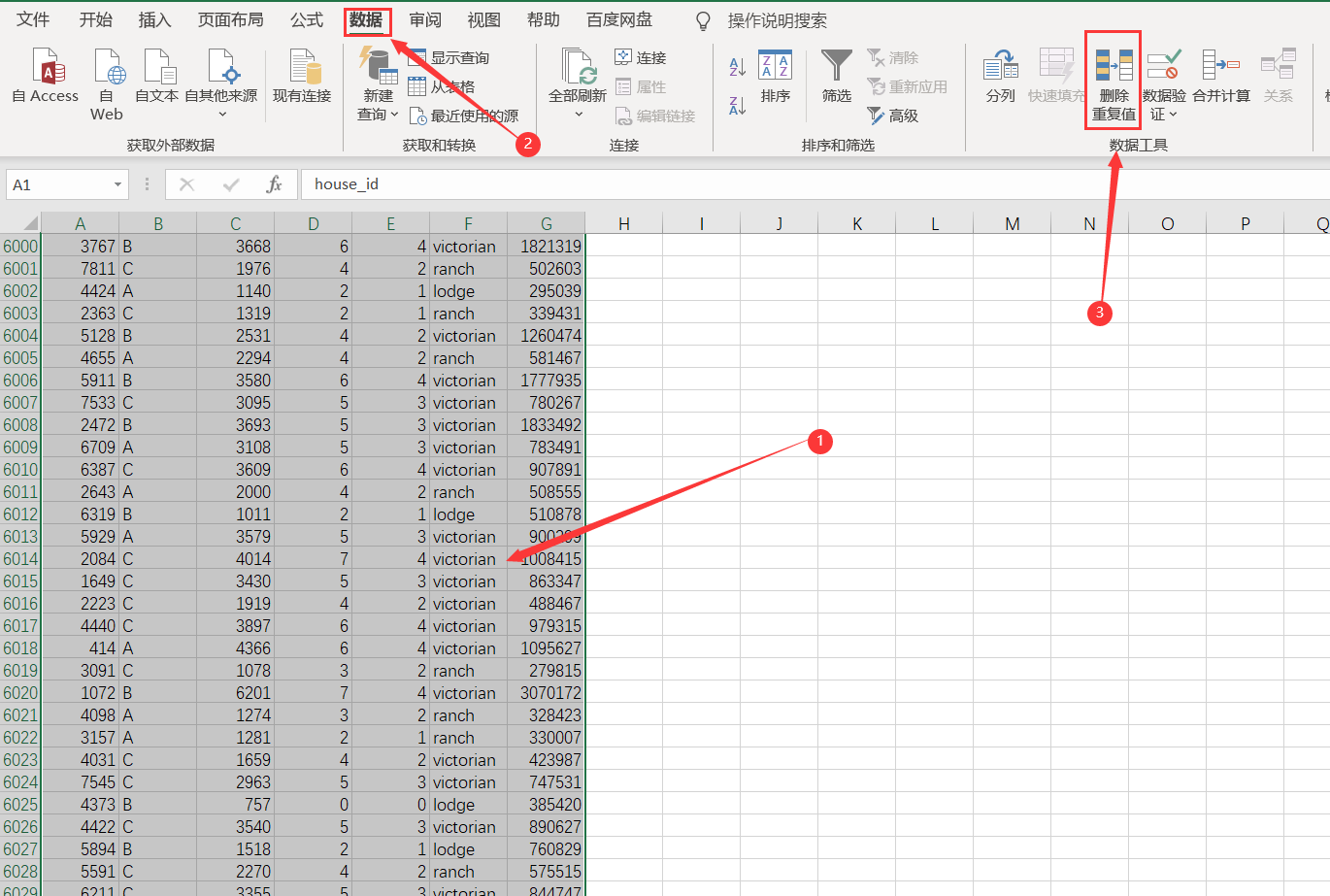
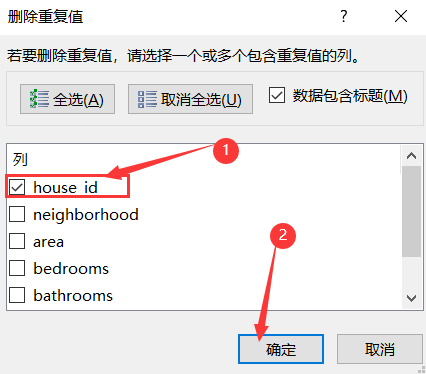
Use unique identification of house_id, delete duplicate values

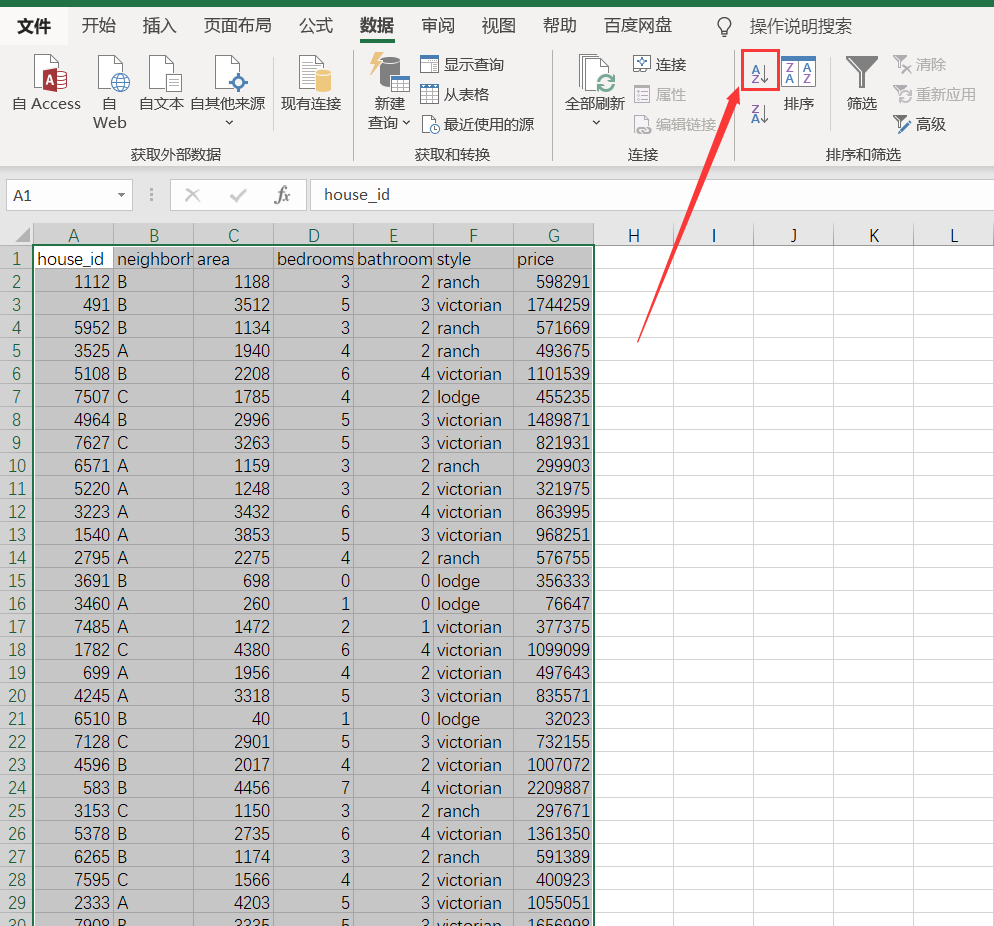
3. Ascending order
In the filter and sort column, select ascending


4. Missing value processing
The data area of the selected address column is the column where bedrooms is located

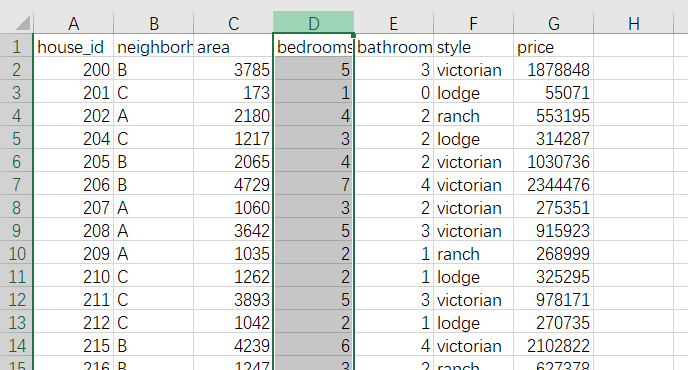
Click data - Filter - drop-down triangle in the figure

The filter value is 0, click OK

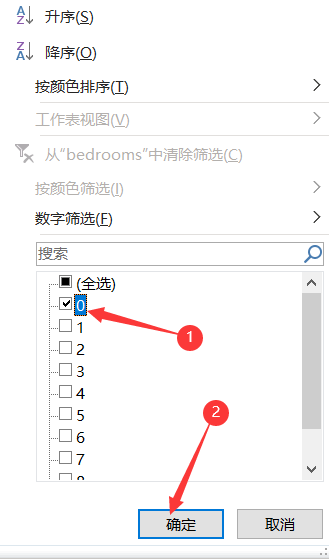
Check to delete all rows with bedrooms value 0

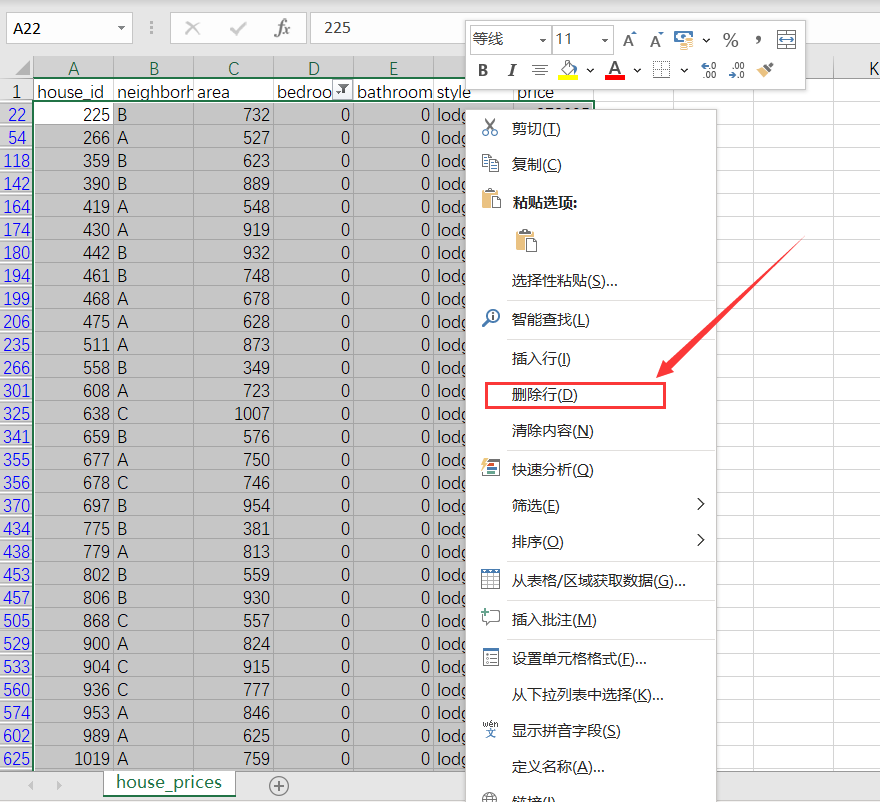
Delete rows with bathrooms value 0 in the same way
Final result:

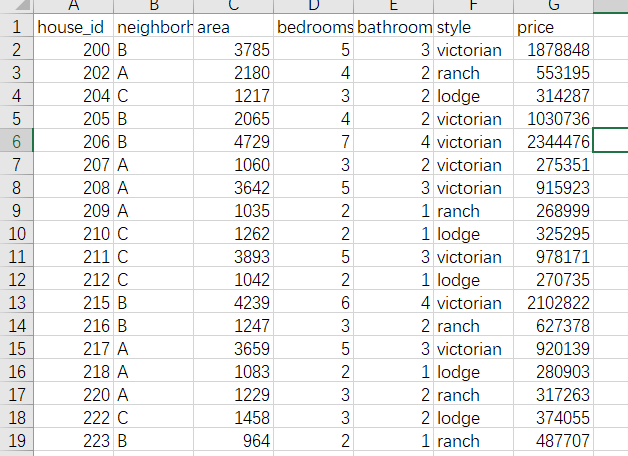
(2) Non numeric data conversion

In the original data, neighborhood and style are non numeric data. It needs to be converted into numerical data before regression analysis can be carried out.

1. Start - find and replace - replace
   
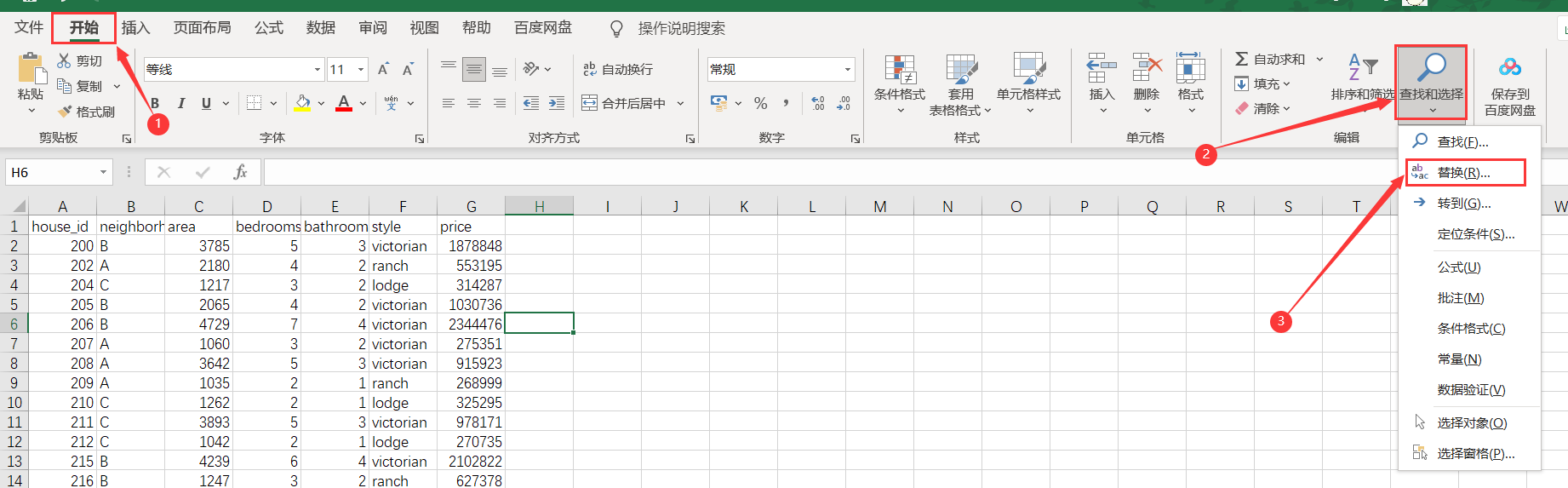
2. Select the column of neighborhood to replace, and replace the A, B and C of the original data with 10, 20 and 30
   
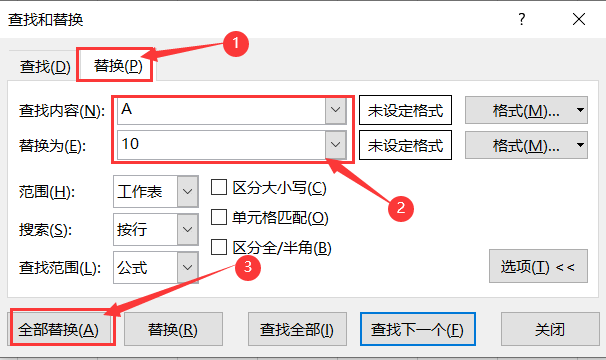
   Replacement succeeded
   
3. Replace style in the same way, and replace the victorian, ranch and lodge of the original data with 100, 200 and 300
   
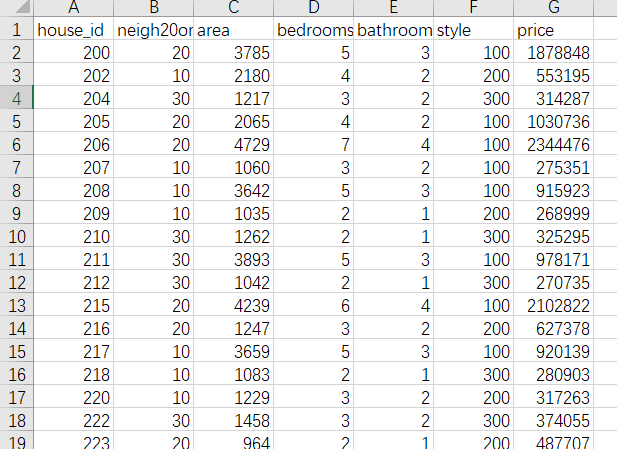
   Replace results
   

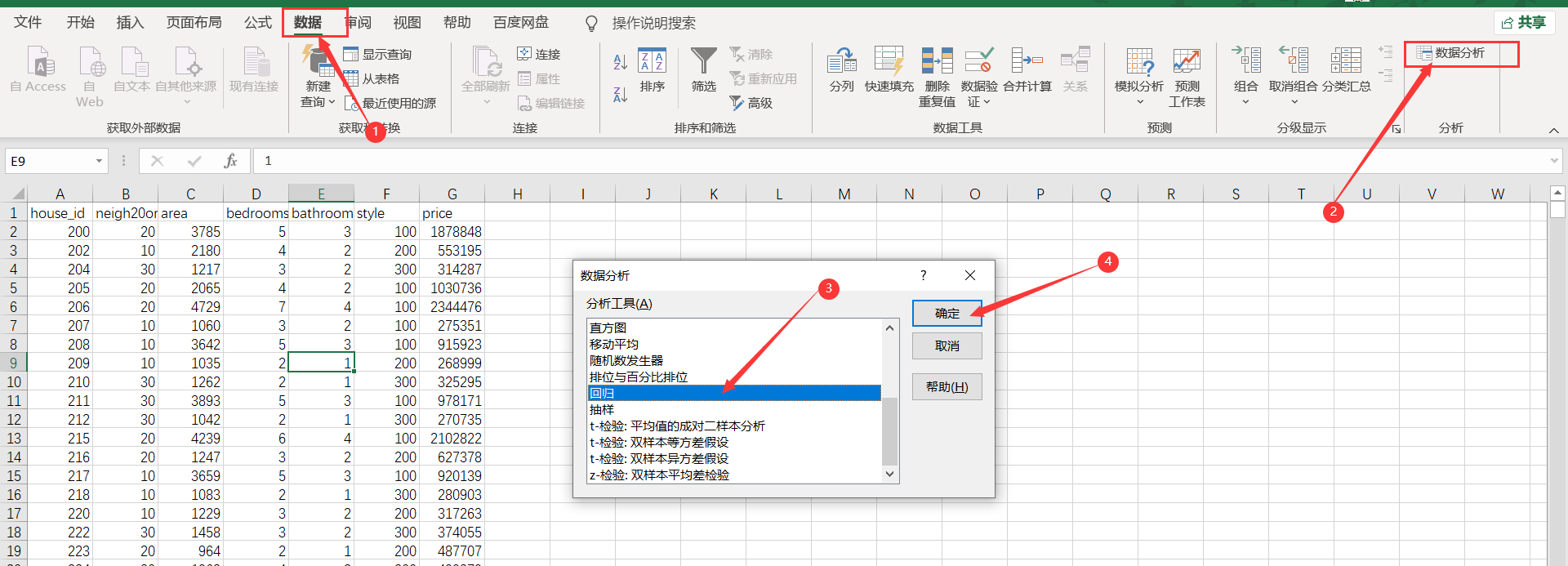
3, Linear regression using EXCEL

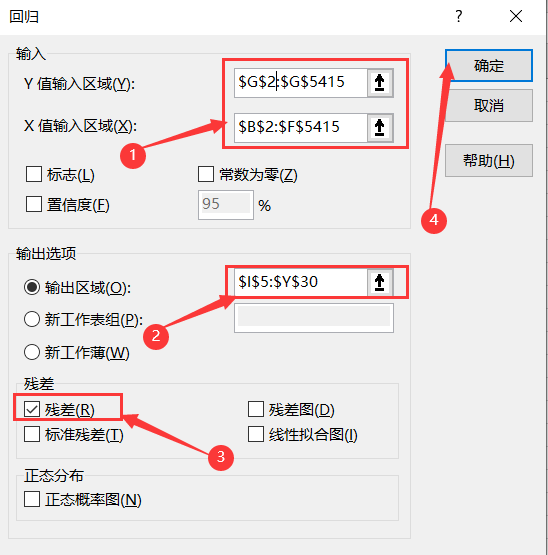
1. Select data, select regression in data analysis, and click OK
   
2. Range with X and Y values

① Enter the interval with price as the Y value
② Take neighborhood, area, bedrooms, bathrooms and style as X values to enter the interval
③ Output display area selection
④ Check residuals
⑤ Click OK

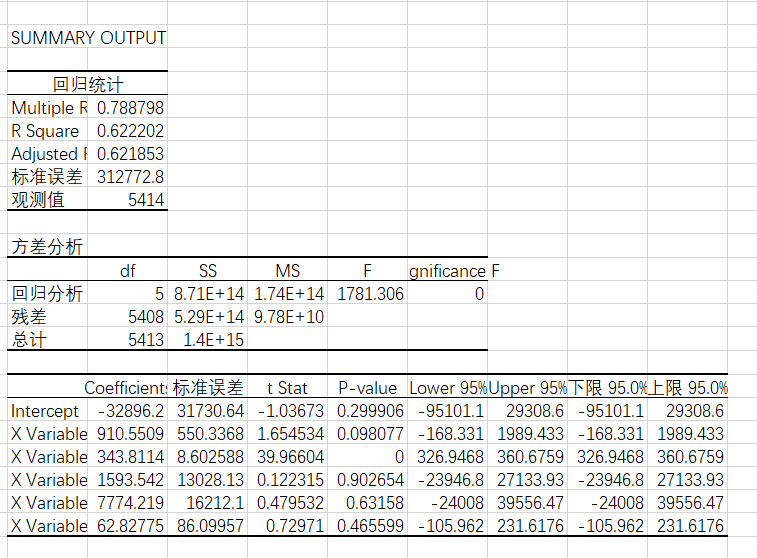
3. Output results

4, Analysis in Python

(1) Without the help of sklearn Library

1. Basic package and data import

1. Import package

import pandas as pd
import numpy as np
import seaborn as sns
import matplotlib.pyplot as plt

1. Read file house_prices.csv 'data

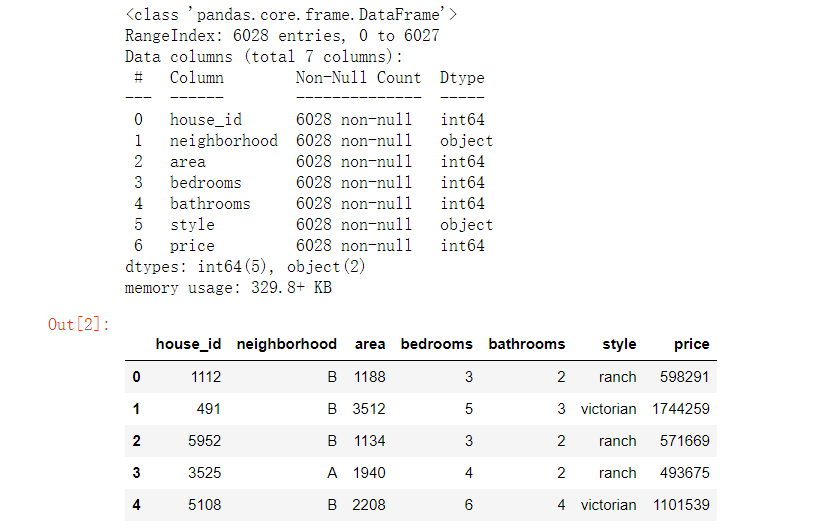
df = pd.read_csv('D:/house_prices.csv')
df.info(); df.head()

Output results:

2. Variable exploration

1. data processing

# Outlier handling
# ================Outlier test function: two methods of IQR & Z score=========================
def outlier_test(data, column, method=None, z=2):
    """ Based on a column, the upper and lower truncation point method is used to detect outliers(Indexes) """
    """ 
    full_data: Complete data
    column: full_data Specified line in, format 'x' Quoted
    return Optional; outlier: Outlier data frame 
    upper: Upper truncation point;  lower: Lower truncation point
    method: Method of checking outliers (optional), default None Is the upper and lower cut-off point method),
            choose Z Method, Z The default is 2
    """
    # ==================Upper and lower cut-off point method to test outliers==============================
    if method == None:
        print(f'with {column} Based on the column, the upper and lower cut-off point method is used(iqr) Detect outliers...')
        print('=' * 70)
        # Quartile; There will be exceptions when calling the function here
        column_iqr = np.quantile(data[column], 0.75) - np.quantile(data[column], 0.25)
        # 1, 3 quantiles
        (q1, q3) = np.quantile(data[column], 0.25), np.quantile(data[column], 0.75)
        # Calculate upper and lower cutoff points
        upper, lower = (q3 + 1.5 * column_iqr), (q1 - 1.5 * column_iqr)
        # Detect outliers
        outlier = data[(data[column] <= lower) | (data[column] >= upper)]
        print(f'First quantile: {q1}, Third quantile:{q3}, Interquartile range:{column_iqr}')
        print(f"Upper cutoff point:{upper}, Lower cutoff point:{lower}")
        return outlier, upper, lower
    # =====================Z-score test outliers==========================
    if method == 'z':
        """ Based on a column, the incoming data is the same as the data you want to segment z Score point, return the outlier index and the data frame """
        """ 
        params
        data: Complete data
        column: Specified detection column
        z: Z Quantile, The default is 2, according to z fraction-According to the normal curve table, take 2 at the left and right ends%，
           According to you z Positive and negative setting of scores. It can also be changed arbitrarily to know the data set of any top percentage
        """
        print(f'with {column} List as basis, use Z Fractional method, z Quantile extraction {z} To detect outliers...')
        print('=' * 70)
        # Calculate the numerical points of the two Z fractions
        mean, std = np.mean(data[column]), np.std(data[column])
        upper, lower = (mean + z * std), (mean - z * std)
        print(f"take {z} individual Z Score: greater than {upper} Or less than {lower} Is considered an outlier.")
        print('=' * 70)
        # Detect outliers
        outlier = data[(data[column] <= lower) | (data[column] >= upper)]
        return outlier, upper, lower

1. Call function

outlier, upper, lower = outlier_test(data=df, column='price', method='z')
outlier.info(); outlier.sample(5)

1. Delete error data

# Simply discard it here
df.drop(index=outlier.index, inplace=True)

3. Analyze data

1. Define variables

# Category variables, also known as nominal variables
nominal_vars = ['neighborhood', 'style']

for each in nominal_vars:
    print(each, ':')
    print(df[each].agg(['value_counts']).T)
    # Direct. value_counts().T cannot achieve the following effect
     ## You must get agg, and the brackets [] inside can't be less
    print('='*35)
    # It is found that the number of each category is also OK, so as to prepare for the following analysis of variance

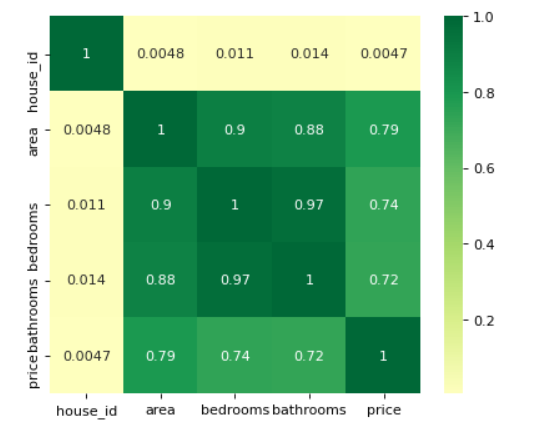
2. Check the correlation of variables in the thermodynamic diagram

# Thermodynamic diagram 
def heatmap(data, method='pearson', camp='RdYlGn', figsize=(10 ,8)):
    """
    data: Whole data
    method: Default to pearson coefficient
    camp: The default is: RdYlGn-Red, yellow and blue; YlGnBu-Yellow green blue; Blues/Greens It's also a good choice
    figsize: The default is 10, 8
    """
    ## Eliminate color blocks with diagonal color duplication
    #     mask = np.zeros_like(df2.corr())
    #     mask[np.tril_indices_from(mask)] = True
    plt.figure(figsize=figsize, dpi= 80)
    sns.heatmap(data.corr(method=method), \
                xticklabels=data.corr(method=method).columns, \
                yticklabels=data.corr(method=method).columns, cmap=camp, \
                center=0, annot=True)
    # To achieve the effect of leaving only half of the diagonal, the parameters in brackets can be added with mask=mask

1. Call function output result

# It can be seen from the thermodynamic diagram that the relationship between variables such as area, bedrooms and bathrooms and house price is still relatively strong
 ## Therefore, it is worth putting into the model, but the relationship between the classification variables style and neighborhood and price is unknown
heatmap(data=df, figsize=(6,5))

4. Fitting

1. Introduce model
In the exploration just now, we found that the categories of style and neighborhood are three categories. If there are only two categories, we can conduct chi square test, so here we use analysis of variance

Using the analysis of variance in the regression model, only stats models have an analysis of variance library to extract the analysis of variance results from the linear regression results

import statsmodels.api as sm
from statsmodels.formula.api import ols # ols is a statistical database for establishing linear regression model
from statsmodels.stats.anova import anova_lm

600 samples were randomly selected from the dataset

df = df.copy().sample(600)

# C means to tell python that this is a classified variable, otherwise Python will use it as a continuous variable
## Here, analysis of variance is directly used to test all classified variables
## The following lines of code are the standard gestures for analysis of variance using the statistical library
lm = ols('price ~ C(neighborhood) + C(style)', data=df).fit()
anova_lm(lm)

# The Residual line indicates the within group that cannot be explained by the model, and the others are between groups that can be explained
# df: degree of freedom (n-1) - the number of categories in the classification variable minus 1
# sum_sq: sum of total squares (SSM), sum of residual lines_ eq: SSE
# mean_ SQ: MSM, mean of residual line_ sq: mse
# F: F statistics, just check the chi square distribution table
# Pr (> F): P value

# Refresh several times and find that they are very significant, so these two variables are also worth putting into the model

Output results:

2. Multiple linear regression modeling

from statsmodels.formula.api import ols

lm = ols('price ~ area + bedrooms + bathrooms', data=df).fit()
lm.summary()

Output results:

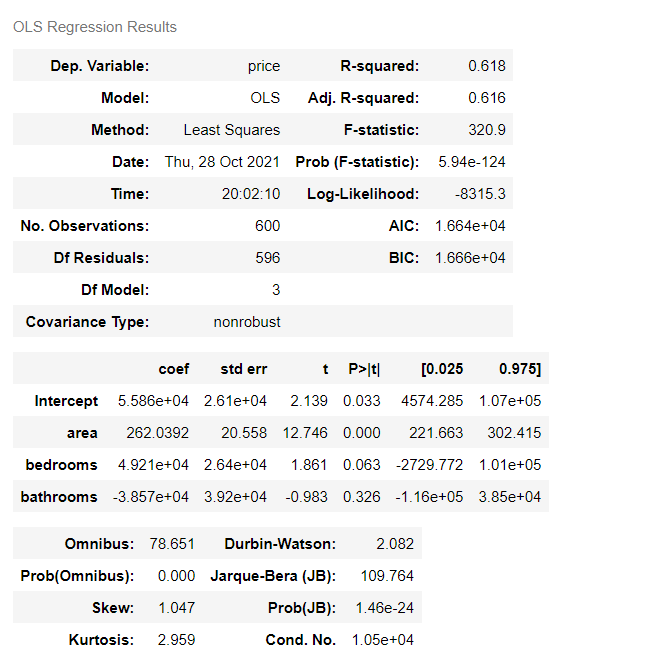
3. Model optimization
It is found that the accuracy is not high enough. Here, the accuracy of the model is improved by adding dummy variables and using variance expansion factor to detect multicollinearity

# Set dummy variable
# Take the nominal variable neighborhood as an example
nominal_data = df['neighborhood']

# Set dummy variable
dummies = pd.get_dummies(nominal_data)
dummies.sample()  # pandas will automatically name it for you

# One dummy variable generated by each nominal variable needs to be discarded. Here, take discarding C as an example
dummies.drop(columns=['C'], inplace=True)
dummies.sample()

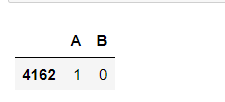
The results are spliced with the original data set

# Splice the results with the original data set
results = pd.concat(objs=[df, dummies], axis='columns')  # Merge by column
results.sample(3)
# You can try to handle the nominal variable style by yourself

Output results:

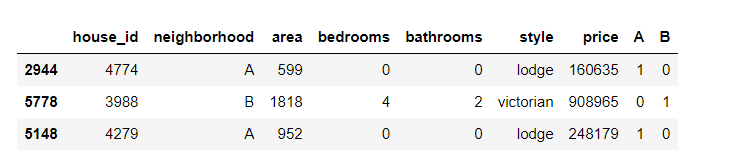
4. Modeling again

# Modeling again
lm = ols('price ~ area + bedrooms + bathrooms + A + B', data=results).fit()
lm.summary()

Output results:

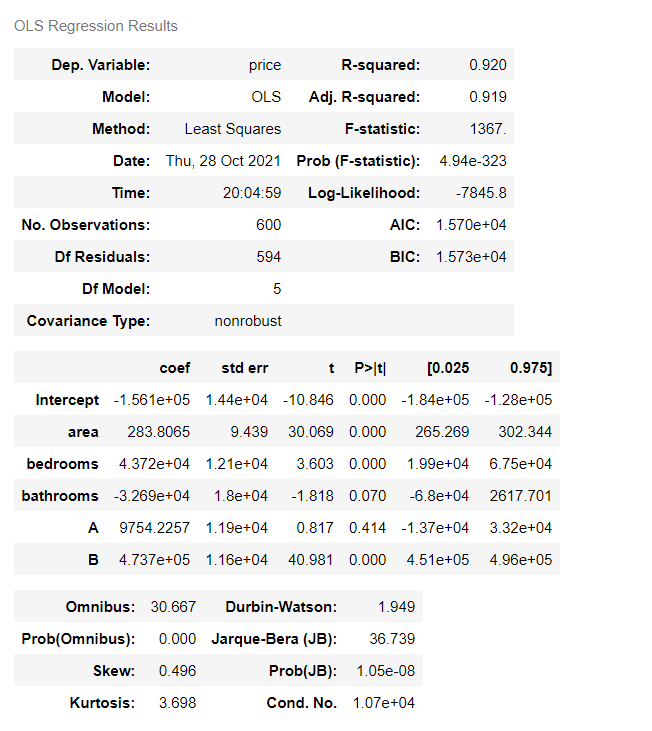
5. Deal with Multicollinearity
Self defined variance expansion factor detection formula

def vif(df, col_i):
    """
    df: Whole data
    col_i: Detected column name
    """
    cols = list(df.columns)
    cols.remove(col_i)
    cols_noti = cols
    formula = col_i + '~' + '+'.join(cols_noti)
    r2 = ols(formula, df).fit().rsquared
    return 1. / (1. - r2)

function call

test_data = results[['area', 'bedrooms', 'bathrooms', 'A', 'B']]
for i in test_data.columns:
    print(i, '\t', vif(df=test_data, col_i=i))
# It is found that there is a strong correlation between bedrooms and bathrooms, which may explain the same problem

Output results:

6. Fit again
The variance expansion factors of bedrooms and bathrooms are higher, which confirms the principle that most variance expansion factors appear in pairs. Here, we can discard bedrooms with larger expansion factors

lm = ols(formula='price ~ area + bathrooms + A + B', data=results).fit()
lm.summary()

Output results:

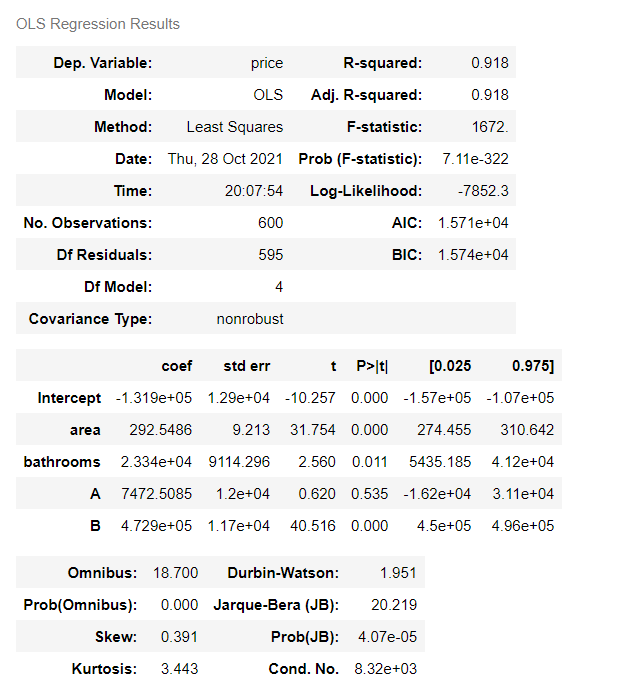
There is still multicollinearity. Test again

test_data = df[['area', 'bathrooms']]
for i in test_data.columns:
    print(i, '\t', vif(df=test_data, col_i=i))

(2) With the help of sklearn Library

1. No data processing

1. Import packages and data

import pandas as pd
import numpy as np
import math
import matplotlib.pyplot as plt # Drawing
from sklearn import linear_model # linear model
data = pd.read_csv('C:/Users/86199/Jupyter/house_prices_second.csv') #Read data
data.head() #Data display

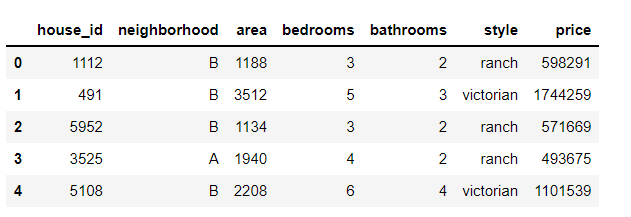
2. Remove the first column of house_id

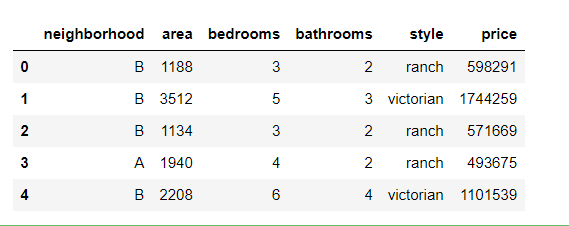
new_data=data.iloc[:,1:] #Get rid of the id column
new_data.head()

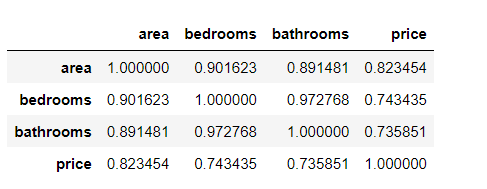
3. Relationship coefficient matrix display

new_data.corr() # Correlation coefficient matrix, only statistical value column

4. Assignment variable

x_data = new_data.iloc[:, 0:5] #Corresponding columns of area, bedrooms and bathroom
y_data = new_data.iloc[:, -1] #price corresponding column
print(x_data, y_data, len(x_data))

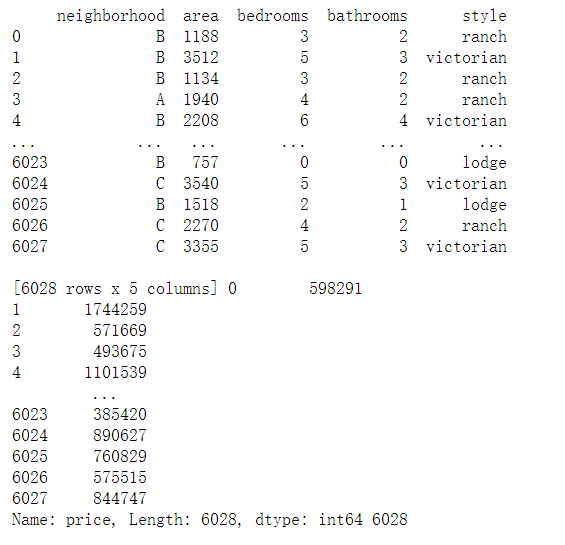
5. Establish the model and output the results

# Application model
model = linear_model.LinearRegression()
model.fit(x_data, y_data)
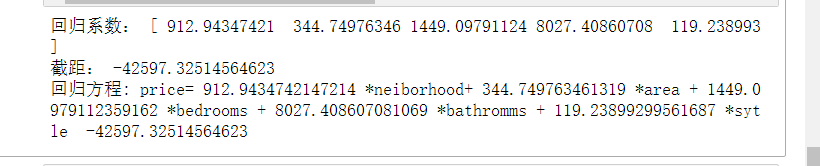
print("Regression coefficient:", model.coef_)
print("Intercept:", model.intercept_)
print('regression equation : price=',model.coef_[0],'*neiborhood+',model.coef_[1],'*area +',model.coef_[2],'*bedrooms +',model.coef_[3],'*bathromms +',model.coef_[4],'*sytle ',model.intercept_)

(2) The data shall be cleaned before solving

1. Assign a new variable

new_data_Z=new_data.iloc[:,0:]
new_data_IQR=new_data.iloc[:,0:]

1. Outlier handling

# ================Outlier test function: two methods of IQR & Z score=========================
def outlier_test(data, column, method=None, z=2):
    """ Based on a column, the upper and lower truncation point method is used to detect outliers(Indexes) """
    """ 
    full_data: Complete data
    column: full_data Specified line in, format 'x' Quoted
    return Optional; outlier: Outlier data frame 
    upper: Upper truncation point;  lower: Lower truncation point
    method: Method of checking outliers (optional), default None Is the upper and lower cut-off point method),
            choose Z Method, Z The default is 2
    """
    # ==================Upper and lower cut-off point method to test outliers==============================
    if method == None:
        print(f'with {column} Based on the column, the upper and lower cut-off point method is used(iqr) Detect outliers...')
        print('=' * 70)
        # Quartile; There will be exceptions when calling the function here
        column_iqr = np.quantile(data[column], 0.75) - np.quantile(data[column], 0.25)
        # 1, 3 quantiles
        (q1, q3) = np.quantile(data[column], 0.25), np.quantile(data[column], 0.75)
        # Calculate upper and lower cutoff points
        upper, lower = (q3 + 1.5 * column_iqr), (q1 - 1.5 * column_iqr)
        # Detect outliers
        outlier = data[(data[column] <= lower) | (data[column] >= upper)]
        print(f'First quantile: {q1}, Third quantile:{q3}, Interquartile range:{column_iqr}')
        print(f"Upper cutoff point:{upper}, Lower cutoff point:{lower}")
        return outlier, upper, lower
    # =====================Z-score test outliers==========================
    if method == 'z':
        """ Based on a column, the incoming data is the same as the data you want to segment z Score point, return the outlier index and the data frame """
        """ 
        params
        data: Complete data
        column: Specified detection column
        z: Z Quantile, The default is 2, according to z fraction-According to the normal curve table, take 2 at the left and right ends%，
           According to you z Positive and negative setting of scores. It can also be changed arbitrarily to know the data set of any top percentage
        """
        print(f'with {column} List as basis, use Z Fractional method, z Quantile extraction {z} To detect outliers...')
        print('=' * 70)
        # Calculate the numerical points of the two Z fractions
        mean, std = np.mean(data[column]), np.std(data[column])
        upper, lower = (mean + z * std), (mean - z * std)
        print(f"take {z} individual Z Score: greater than {upper} Or less than {lower} Is considered an outlier.")
        print('=' * 70)
        # Detect outliers
        outlier = data[(data[column] <= lower) | (data[column] >= upper)]
        return outlier, upper, lower

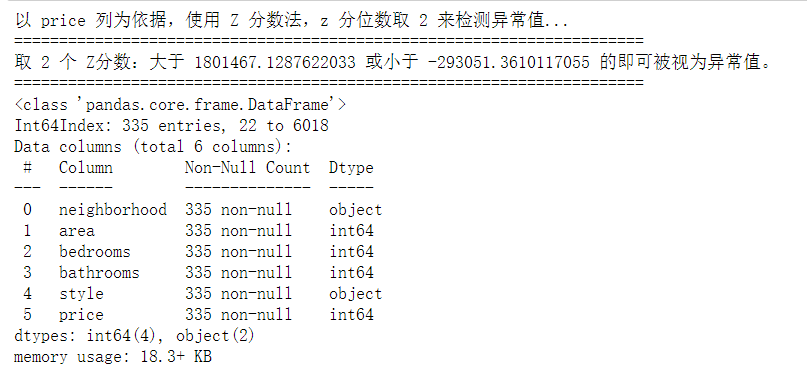
1. Based on the price column, the Z-score method is used, and the z-quantile is taken as 2 to detect outliers

outlier, upper, lower = outlier_test(data=new_data_Z, column='price', method='z')
outlier.info(); outlier.sample(5)

# Simply discard it here
new_data_Z.drop(index=outlier.index, inplace=True)

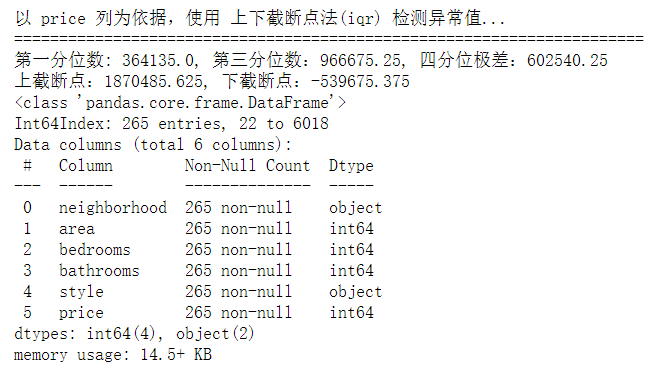
4. Based on the price column, the upper and lower cut-off point method (iqr) is used to detect abnormal values

outlier, upper, lower = outlier_test(data=new_data_IQR, column='price')
outlier.info(); outlier.sample(6)

# Simply discard it here
new_data_IQR.drop(index=outlier.index, inplace=True)

5. Output original data correlation matrix

print("Original data correlation matrix")
new_data.corr()

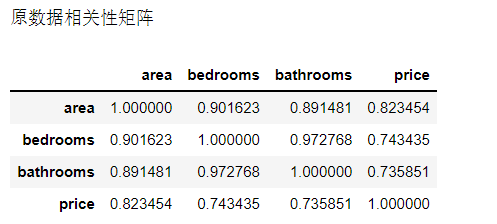
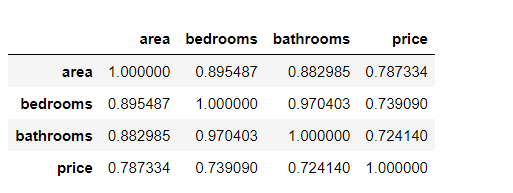
6. Data correlation matrix processed by Z method

#Insert the code slice here
print("Z Data correlation matrix processed by method")
new_data_Z.corr()

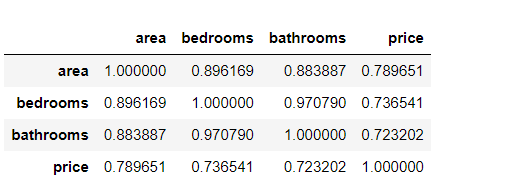
7. Data correlation matrix processed by IQR method

print("IQR Data correlation matrix processed by method")
new_data_IQR.corr()

8. Modeling output

x_data = new_data_Z.iloc[:, 0:5]
y_data = new_data_Z.iloc[:, -1]
# Application model
model = linear_model.LinearRegression()
model.fit(x_data, y_data)
print("Regression coefficient:", model.coef_)
print("Intercept:", model.intercept_)
print('regression equation : price=',model.coef_[0],'*neiborhood+',model.coef_[1],'*area +',model.coef_[2],'*bedrooms +',model.coef_[3],'*bathromms +',model.coef_[4],'*sytle ',model.intercept_)

summary

The first is to understand the related concepts of multiple regression model and the basic steps of constructing the model. By using excel and sklearn library to carry out multiple linear regression, we also feel that multiple linear regression is more practical than univariate linear regression.

reference resources

https://blog.csdn.net/weixin_43196118/article/details/108462140
https://www.cnblogs.com/chouxianyu/p/11704665.html
https://blog.csdn.net/m0_45305539/article/details/111242240