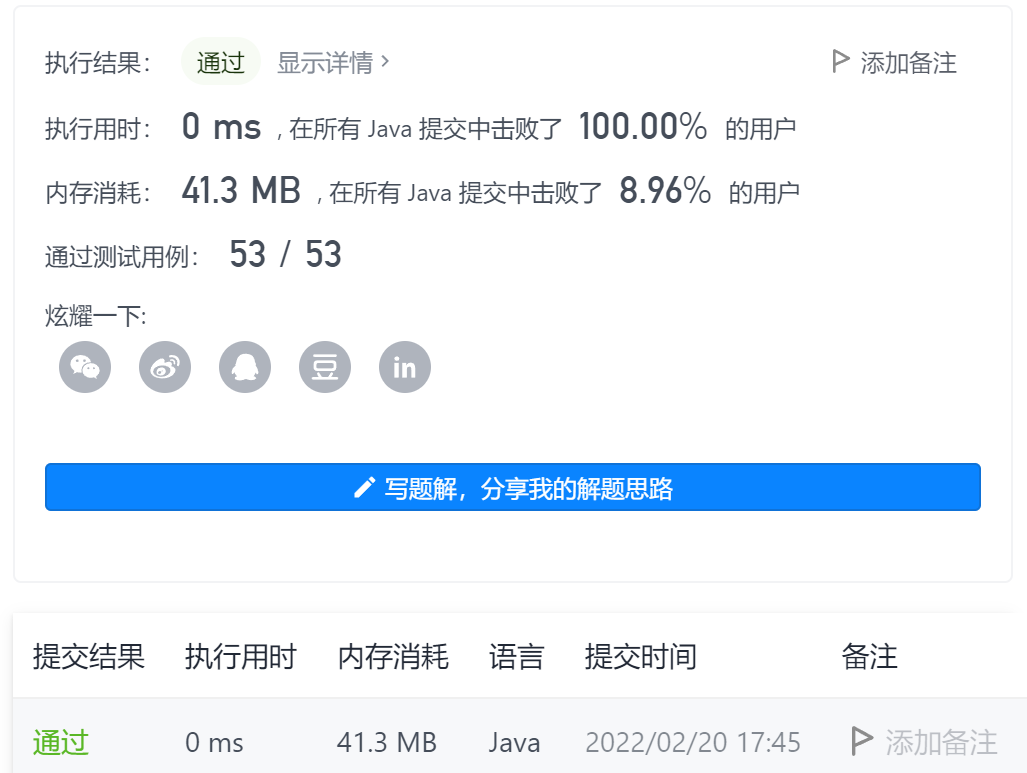
Prefix and brush question summary of leetcode 2
1 - region and retrieval - array immutable
Title Link: Title Link stamp here!!!
Idea: simple prefix sum. During initialization, use the sum array to store the prefix sum of the num array, and then calculate the interval sum from left to right in the num array, which can be obtained directly from sum [right] - sum [left-1] in linear time.
class NumArray {
int [] sums ;
public NumArray(int[] nums) {
sums = new int [nums.length] ;
sums[0] = nums[0] ;
for(int i=1; i<sums.length; i++){
sums[i] = sums[i-1] + nums[i] ;
}
}
public int sumRange(int left, int right) {
if(left>=1){
return sums[right]-sums[left-1] ;
}else {
return sums[right] ;
}
}
}
/**
* Your NumArray object will be instantiated and called as such:
* NumArray obj = new NumArray(nums);
* int param_1 = obj.sumRange(left,right);
*/
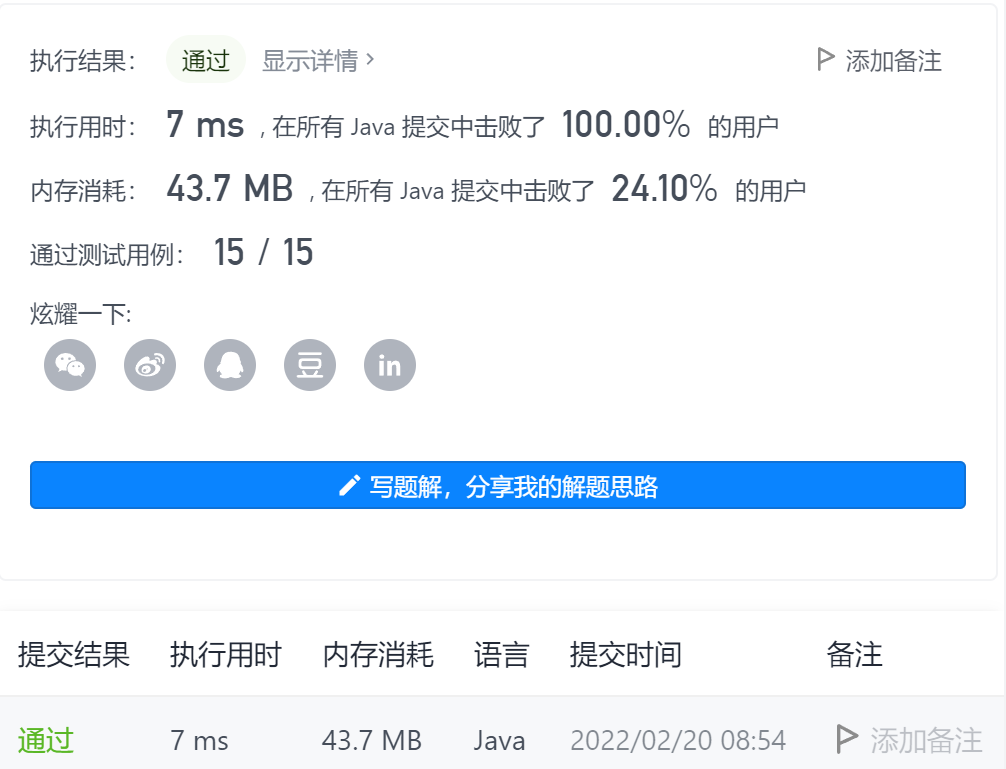
2-2d interval and retrieval - immutable matrix
Title Link: Title Link stamp here!!!
Idea: transform the two-dimensional prefix sum into one-dimensional prefix sum according to each line, then sum the intervals for each line, and then accumulate.
class NumMatrix {
int [][] matrix ;
public NumMatrix(int[][] matrix) {
for(int i=0; i<matrix.length; i++){
for(int j=1; j<matrix[0].length; j++){
matrix[i][j] += matrix[i][j-1] ;//Transform by line into one-dimensional prefix and
}
}
this.matrix = matrix ;
}
public int sumRegion(int row1, int col1, int row2, int col2) {
int sum = 0 ;
for(int i=row1; i<=row2; i++){ //For each row, find the interval sum between the two columns
if(col1-1>=0){
sum += matrix[i][col2] - matrix[i][col1-1] ;
}else{
sum += matrix[i][col2] ;
}
}
return sum ;
}
}
/**
* Your NumMatrix object will be instantiated and called as such:
* NumMatrix obj = new NumMatrix(matrix);
* int param_1 = obj.sumRegion(row1,col1,row2,col2);
*/
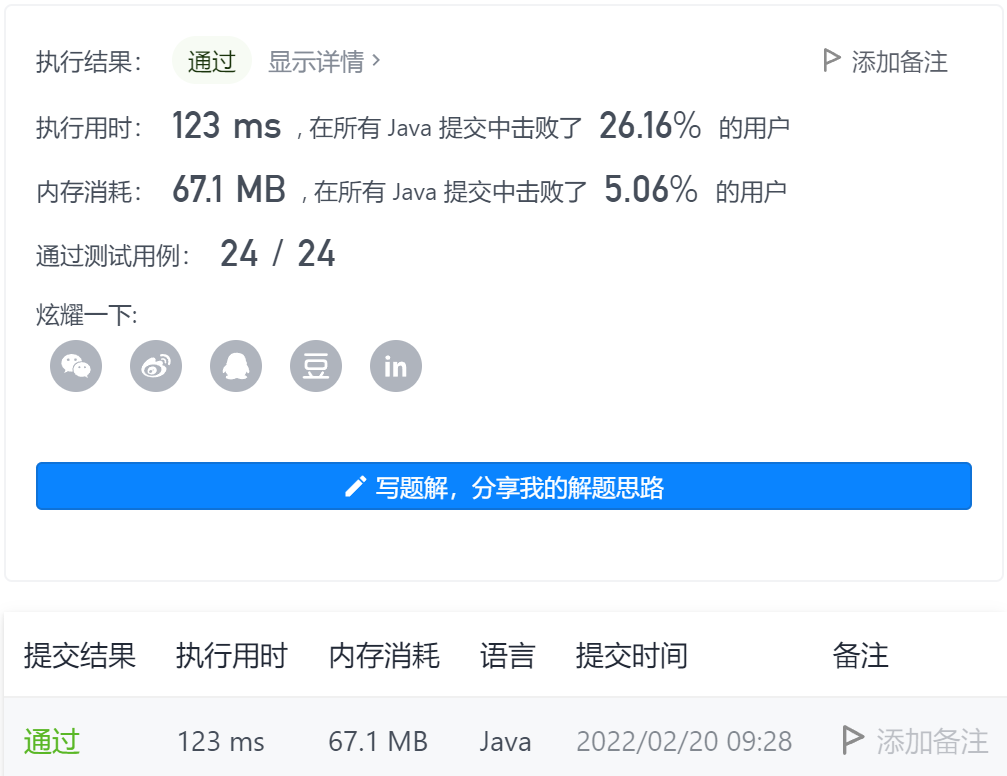
3-matrix area and
Title Link: Title Link stamp here!!!
Idea: this problem uses two-dimensional interval and formula. Just from the perspective of problem solving pile, remember the formula and you can solve the answer immediately.
The matrix interval and formula are as follows:
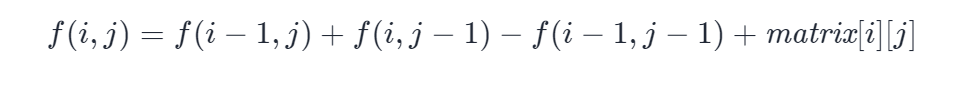
The corresponding mapping formula is as follows:
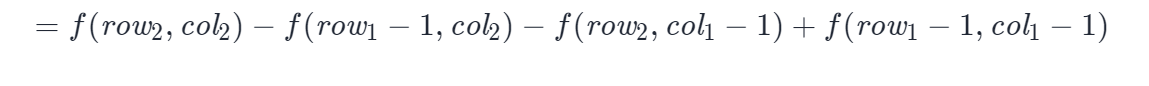
class Solution {
public int[][] matrixBlockSum(int[][] mat, int k) {
//This question needs to use the two digit prefix and. Just remember the formula
int m = mat.length ;
int n = mat[0].length ;
int [][] f = new int [m+1][n+1] ;
for(int i=0; i<m; i++){
for(int j=0; j<n; j++){
f[i+1][j+1] = f[i][j+1] + f[i+1][j] - f[i][j] + mat[i][j] ;
}
}
int [][] res = new int [m][n] ;
for(int i=0; i<m; i++){
for(int j=0; j<n; j++){
int row1 = Math.max(0,i-k) ;
int col1 = Math.max(0,j-k) ;
int row2 = Math.min(i+k,m-1) ;
int col2 = Math.min(j+k,n-1) ;
res[i][j] = f[row2+1][col2+1] - f[row1][col2+1] - f[row2+1][col1] + f[row1][col1] ;
}
}
return res ;
}
}
4 - carpooling
Title Link: Title Link stamp here!!!
Idea: use the site array to record the number of people getting on and off at time I, site[i], and then traverse the site array to find the number of people on the bus at each time. If it is greater than capcity, it will be overloaded.
class Solution {
public boolean carPooling(int[][] trips, int capacity) {
int [] site = new int [1001] ;
for(int []trip : trips){
site[trip[2]] -= trip[0] ;
site[trip[1]] += trip[0] ;
}
int total = 0 ;
for(int people : site){
total += people ;
if(total>capacity){
return false ;
}
}
return true ;
}
}
5 - flight reservation statistics
Title Link: Title Link stamp here!!!
Idea: differential array + prefix and
Notice that a reservation record actually represents an increment of an interval. Our task is to add these increments to get the answer. Therefore, we can use difference decomposition to solve this problem.
The corresponding concept of difference array is prefix and array. For array [1,2,2,4], its difference group is [1,1,0,2]. The i-th number of difference array is the difference between the i-th element and i-1 element of the original array, that is, we can get the original array by summing the prefix of the difference group.
Each row of bookings two-dimensional array has three numbers. The first two numbers represent the left and right end points of the flight interval, and the last number represents the quantity. This quantity is only "valid" for flights in the interval. Therefore, carry out + operation at the left end point and - operation at the first position at the end of the interval, and then calculate the prefix sum of the difference group.
For example, the three numbers [2,4,10] show that 10 positions are reserved from flight numbers 2, 3 and 4, so the number of 10 is only valid for 2, 3 and 4. At 2 points in the difference group + 10, at 5 points in the difference group, 10 loses its function, and 10 can be subtracted.
class Solution {
public int[] corpFlightBookings(int[][] bookings, int n) {
int [] ans = new int [n] ;
for(int [] book : bookings){
ans[book[0]-1] += book[2] ;
if(book[1] < n){
ans[book[1]] -= book[2] ;
}
}
for(int i=1; i<n; i++){
ans[i] += ans[i-1] ;
}
return ans ;
}
}
6-subarray XOR query
Title Link: Title Link stamp here!!!
Idea: use the prefix array to find the XOR value between the current position and all previous elements, and then remove the XOR value of the interval in each query.
class Solution {
public int[] xorQueries(int[] arr, int[][] queries) {
int [] prefix = new int [arr.length] ;
prefix[0] = arr[0] ;
for(int i=1; i<arr.length; i++){
prefix[i] = prefix[i-1] ^ arr[i] ;
}
int [] res = new int [queries.length] ;
for(int i=0; i<queries.length; i++){
if(queries[i][0]-1>=0){
res[i] = prefix[queries[i][1]] ^ prefix[queries[i][0]-1] ;
}else{
res[i] = prefix[queries[i][1]] ;
}
}
return res ;
}
}
7 - sum of all odd length subarrays
Title Link: Title Link stamp here!!!
Idea: find the prefix sum of array elements, and then accumulate the interval sum of odd numbers.
class Solution {
public int sumOddLengthSubarrays(int[] arr) {
int [] sums = new int [arr.length] ;
sums[0] = arr[0] ;
for(int i=1; i<arr.length; i++){
sums[i] = sums[i-1] + arr[i] ;
}
int res = 0 ;
for(int i=-1; i<sums.length; i++){
for(int j=i+1; j<sums.length; j+=2){
if(i==-1){
res += sums[j] ;
}else{
res += sums[j] - sums[i] ;
}
}
}
return res ;
}
}
8 - longest period of good performance
Title Link: Title Link stamp here!!!
Train of thought 1: Violence Law
Because there are few test cases for this problem and there is no requirement for time, the execution time of 2.4s has also passed.
class Solution {
public int longestWPI(int[] hours) {
int ans = 0 ;
for(int i=0; i<hours.length; i++){
int tireDay = 0, freeDay = 0 ;
for(int j=i; j<hours.length; j++){
if(hours[j]>8){
tireDay++ ;
}else{
freeDay++ ;
}
if(tireDay>freeDay){
ans = Math.max(ans, tireDay+freeDay) ;
}
}
}
return ans ;
}
}
Idea 2: prefix sum + monotone stack
Taking the input example hours = [9, 9, 6, 0, 6, 6, 9] as an example, we record a day with more than 8 hours as 1 point and a day with less than or equal to 8 hours as − 1 point. Then, after processing, we get hours = [1, 1, - 1, - 1, - 1, 1], and then we calculate the prefix and presum = [0, 1, 2, 1, 0, -1, -2, -1] (the first bit of the array is set to 0: it is used as a comparison standard of the following monotone stack to select negative numbers and strictly monotone subtraction).
The title requires to return the maximum length of the time period with good performance, that is, find the number of score 1 in the longest period that is greater than the number of score − 1, that is, find the longest sub array in the hour array, and its sum is greater than 0, that is, find the prefix and the two indexes I and j in the array presum, so as to maximize j - i and ensure that presum[j] - presum[i] is greater than 0. At this point, we will turn this problem into: finding the longest uphill in the presum array can be realized by monotone stack.
Maintain a monotone stack in which the element index in presum is stored. The elements pointed to by the index in the stack are strictly monotonically decreasing. The monotone stack is obtained from the presum array as stack = [0, 5, 6], which indicates that the elements are [0, - 1, - 2]. Then we traverse the presum array from back to front and compare it with the elements pointed to by the index at the top of the stack. If the subtraction result is greater than 0, we will go out of the stack until it is not greater than 0, and then update the current maximum width.
class Solution {
public int longestWPI(int[] hours) {
int [] presum = new int [hours.length+1] ;
for(int i=0; i<hours.length; i++){
hours[i] = hours[i]>8 ? 1 : -1 ;
}
for(int i=1;i<presum.length; i++){
presum[i] = presum[i-1] + hours[i-1] ;
}
Stack<Integer> stack = new Stack<>() ;
int result = 0 ;
stack.push(0) ;
for(int i=1; i<presum.length; i++){
if(stack.isEmpty() || presum[stack.peek()] > presum[i]){
stack.push(i) ;
}
}
for(int i=presum.length-1; i>=0; i--){
while(!stack.isEmpty() && presum[i] > presum[stack.peek()]) {
result = Math.max(result, i - stack.pop());
}
}
return result ;
}
}
9-sum of absolute values of difference in ordered array
Title Link: Title Link stamp here!!!
Idea: prefix and + find rules
class Solution {
public int[] getSumAbsoluteDifferences(int[] nums) {
int [] sums = new int [nums.length+1] ;
for(int i=1; i<sums.length; i++){
sums[i] = sums[i-1] + nums[i-1] ;
}
int [] result = new int [nums.length] ;
for(int i=1; i<sums.length; i++){
int left = i * nums[i-1] - sums[i] ;
int right = sums[sums.length-1] - sums[i] - (sums.length-1-i) * nums[i-1] ;
result[i-1] = left + right ;
}
return result ;
}
}
Dynamic sum of 10-one-dimensional arrays
Title Link: Title Link stamp here!!!
The library is closing. It's too early to close today. It's an easy question. It's over!!!
class Solution {
public int[] runningSum(int[] nums) {
int [] res = new int [nums.length] ;
res[0] = nums[0] ;
for(int i=1; i<nums.length; i++){
res[i] = res[i-1] + nums[i] ;
}
return res ;
}
}