Fishing:
M # m # 211. Adding and searching words - data structure design
Difficulty: medium
Please design a data structure that supports adding new words and finding whether the string matches any previously added string.
Implement dictionary class WordDictionary :
- WordDictionary() Initialize dictionary object
- void addWord(word) take word Add to the data structure and match it later
- bool search(word) If there is a string in the data structure and word Match, return true ; Otherwise, return false . word May contain some '.' , each . Can represent any letter.
Example:
Input:
["WordDictionary","addWord","addWord","addWord","search","search","search","search"]
[[],["bad"],["dad"],["mad"],["pad"],["bad"],[".ad"],["b.."]]
Output:
[null,null,null,null,false,true,true,true]
Explanation:
WordDictionary wordDictionary = new WordDictionary();
wordDictionary.addWord("bad");
wordDictionary.addWord("dad");
wordDictionary.addWord("mad");
wordDictionary.search("pad"); // return False
wordDictionary.search("bad"); // return True
wordDictionary.search(".ad"); // return True
wordDictionary.search("b.."); // return True
Tip: 1 < = word. Length < = 500
word in addWord consists of lowercase English letters
word in search consists of '.' or lowercase English letters
addWord and search can be called up to 50000 times
At first, I wanted to use array: (solution of timeout)
List<String> lists;
public WordDictionary() {
this.lists = new ArrayList<>();
}
public void addWord(String word) {
lists.add(word);
}
public boolean search(String word) {
int i;
for (i = 0; i < lists.size(); i++) {
String str = lists.get(i);
if (str.length() != word.length()){
continue;
}
int j;
for ( j= 0; j < word.length(); j++) {
if (word.charAt(j)=='.'){
continue;
}else {
if (word.charAt(j)!=str.charAt(j)){
break;
}
}
}
if (j == word.length()){
break;
}
}
if (i == lists.size()){
return false;
}else {
return true;
}
}
The positive solution is to use the prefix tree:
What is a prefix tree (dictionary tree):
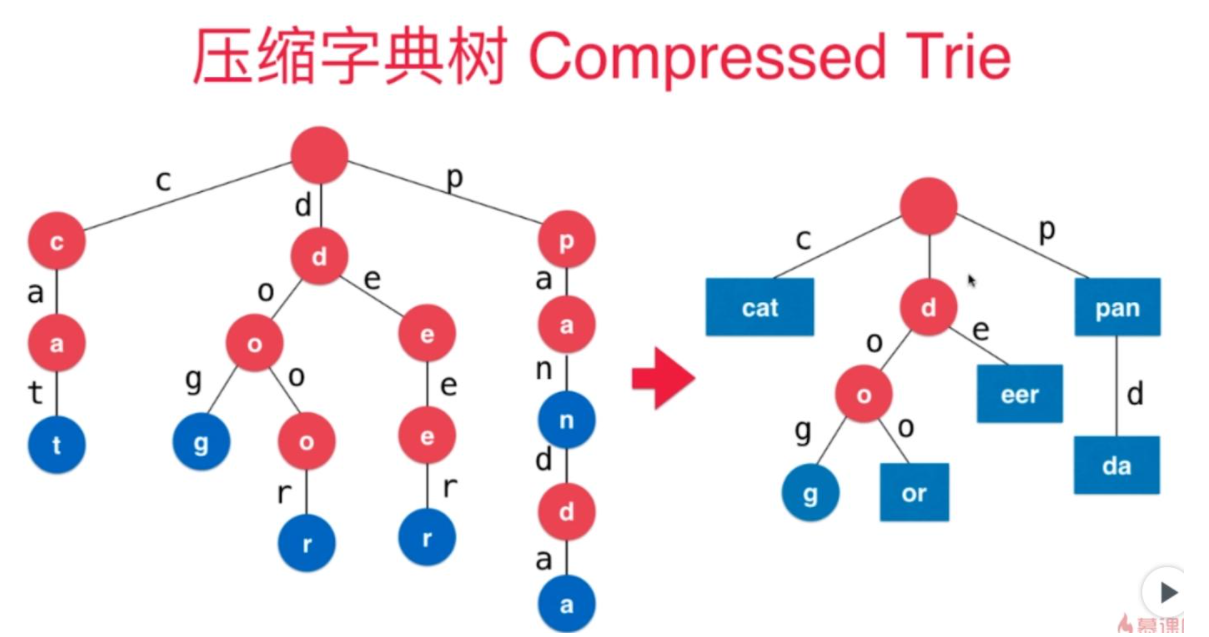
Just like a dictionary, it is easy to find and reduce the time complexity of query (the time complexity of heap sorting is O(n*log n)). The time complexity of prefix tree will be lower, because the children of nodes are generally larger than two. In fact, prefix tree can be regarded as a multi subtree (binary tree).
likou211: prefix tree solution code:
public class WordDictionary {
Tree tree;
public WordDictionary() {
this.tree = new Tree();
}
public void addWord(String word) {
tree.insert(word);
}
public boolean search(String word) {
return BFS(word,0,tree);
}
private boolean BFS(String word, int i, Tree tree) {
if (word.length() == i){
return tree.inEnd();
}
char ch = word.charAt(i);
int index = ch - 'a';
if (Character.isLetter(ch)){
if (tree.getChildren()[index] !=null && BFS(word,i+1,tree.getChildren()[index])){
return true;
}
}else {
for (int j = 0; j < 26; j++) {
if (tree.getChildren()[j] !=null && BFS(word,j+1,tree.getChildren()[index])){
return true;
}
}
}
return false;
}
class Tree{
boolean isEnd = false;
Tree[] trees = new Tree[26];
public void insert(String word){
Tree tree = this;
for (int i = 0; i < word.length(); i++) {
char ch = word.charAt(i);
int index = ch - 'a';
if (tree.trees[index] == null){
tree.trees[index] = new Tree();
}
tree = tree.trees[index];
}
tree.isEnd = true;
}
public boolean inEnd(){
return isEnd;
}
public Tree[] getChildren() {
return trees;
}
}
public static void main(String[] args) {
WordDictionary wordDictionary = new WordDictionary();
wordDictionary.addWord("abc");
System.out.println(wordDictionary.search("abz"));
}
}
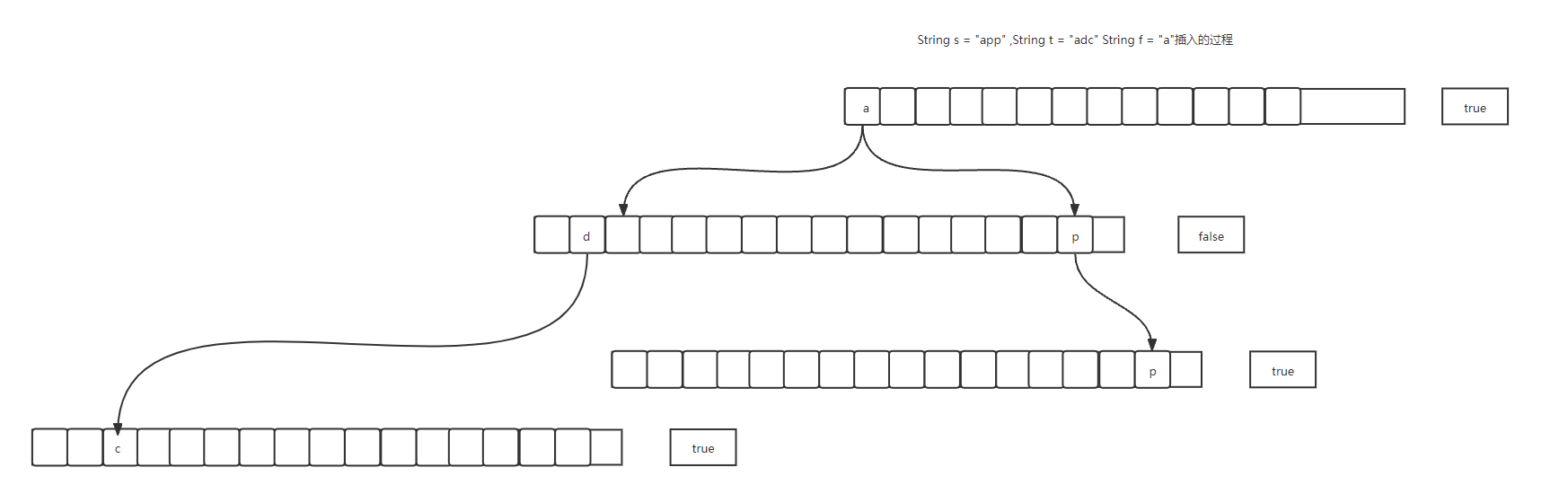
The first step is to create a Tree class. There are two properties in the class. One is
boolean isEnd = false; Mark whether it is the end of a word. If it is the end of a word, it is true
Tree[] trees = new Tree[26]; This can hold 26 letters, through

if (tree.trees[index] == null){
tree.trees[index] = new Tree(); // When inserting, the character is null (this is through the pointer)
//By overwriting the address of a position on the array, it is the same as the c language pointer
}
likou211;
The code roughly means
one Create a prefix tree, which is defined in advance
Tree tree;
public WordDictionary() {
this.tree = new Tree();
}
two Add words directly to the data structure of the prefix tree
public void addWord(String word) {
tree.insert(word);
}
3. Query whether the word is in the data structure
public boolean search(String word) {
return BFS(word,0,tree);
}
BFS: depth traversal
When the word length is equal to the traversal depth, check whether the word has been inserted and whether isEnd is true
if (Character.isLetter(ch)){
if (tree.getChildren()[index] !=null && BFS(word,i+1,tree.getChildren()[index])){
return true;
}
}
If the character is a letter, judge whether there is a corresponding child. If false is not returned, move the word backward by one bit, continue to search until it moves to the last bit of the word, and judge whether isEnd is true
else {
for (int j = 0; j < 26; j++) {
if (tree.getChildren()[j] !=null && BFS(word,j+1,tree.getChildren()[index])){
return true;
}
}
}
If the character is'. ', you need to traverse a-z all the words, and then do the same as before
Let's assume to find string a = "a", string B = "A.P", string c = "ass";
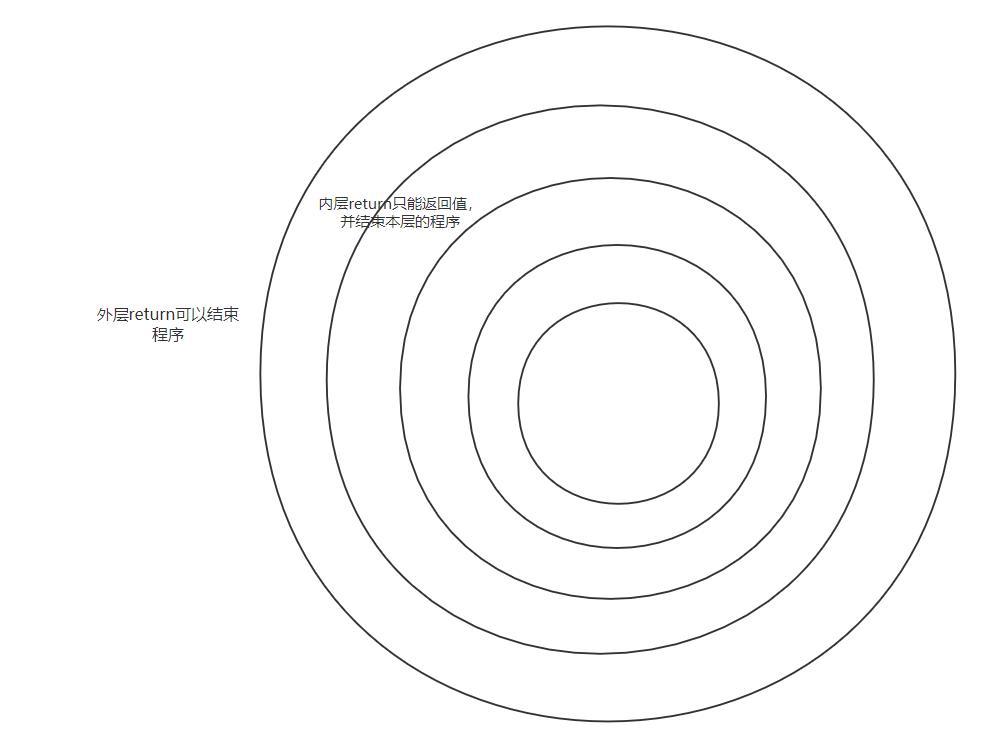
The recursion diagram is as follows. Recursion is just like tape (like watering pipes). It will approach inside layer by layer, and finally come out from the innermost side. In fact, if the return of the inner layer is false, it will traverse all the time (because the if conditions are all true). If the return is true, the program will end the for loop, and then return to the upper layer. Here, the if condition is also true, So it holds until the outermost layer returns true