Prim algorithm

Prim algorithm is an algorithm to find the minimum spanning tree (mst) through the connected network
Process:
1. Firstly, select any vertex as the root of the tree
2. Traverse other vertices (not in the tree). For each vertex, find an edge with the shortest path to mst. In this way, each vertex has an edge to mst (if it is not adjacent, set the weight to infinity)

Here, the path means the direct distance between two vertices. For non adjacent vertices, the path distance is ∞, otherwise it is the weight of this edge

3. Among all the edges, find the one with the smallest weight and add the corresponding vertex to mst
Cycle 2, 3 (cycle n-1 times for n vertices)


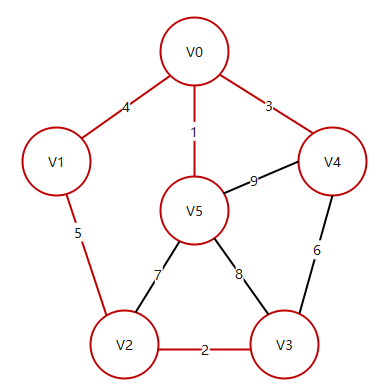
For example, find the minimum spanning tree in the figure below

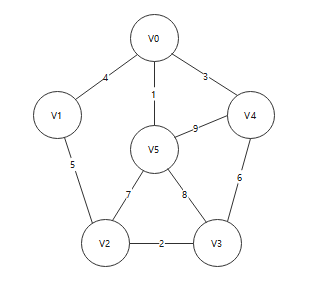
Firstly, v0 is selected as the starting point, and the distances from other vertices to mst are [0, 4, ∞, ∞, 3, 1] respectively

Select the smallest of the six edges (non-zero) (v0, v5) and add v5 to mst:

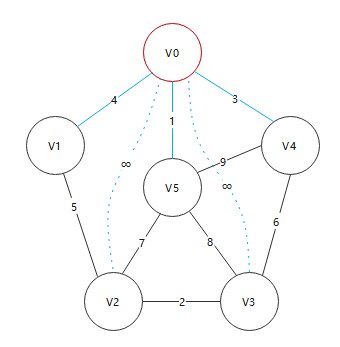
Then, repeat the above steps. The minimum distance from each vertex to mst is: [0, 4, 7, 8, 3, 0]

v2 selects (v2, v5) from (v2, v0) and (v2, v5), and the distance from the tree is updated from the original infinity to 7. Similarly, v3 is updated from ∞ to 8

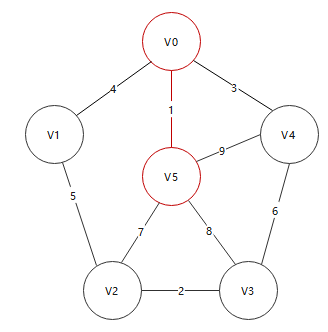
Select the edges from V4 to non-zero, and add them from v4
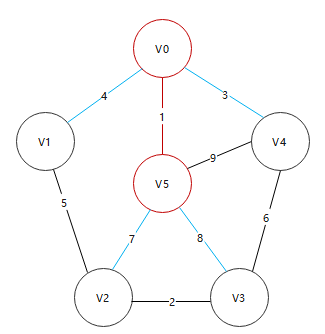
... keep cycling, and the final result is as follows:

code implementation

Use adjacency table to store graph structure:

typedef struct EdgeNode{
    int adjIndex;   //Adjacency to vertex with subscript adjindex
    WEIGHT weight;
    struct EdgeNode * next;
}EdgeNode;			//Edge node

typedef struct VertexNode{
    DataElement data;
    int id;
    EdgeNode* firstEdge;
}VertexNode;		//Vertex node

typedef struct AdjList{
    VertexNode* VerNode[MAXSIZE];
    int verQuantity;    //Number of vertices
    int edgeQuantity;   //Number of edges
}AdjList;

Creating a minimum spanning tree requires three auxiliary arrays:

• bool isAdded[MAXSIZE]
• int lowcost[MAXSIZE]
• int adjVex[MAXSIZE]

isAdded stores whether a fixed point has been added to mst

This array is not available in the adjacency matrix representation, because 0 and INFINITY can be used in the adjacency matrix to indicate that the vertex has been added to mst and the edge weight is infinite, while in the adjacency table representation, the edge weight can only be indicated by pointing to NULL through the pointer, so an auxiliary array isAdded is required

Lowcast stores the shortest path from a node to mst

For example, mst has three vertices a, B and C. at this time, there are three paths from a non mst vertex d to mst: (A,D),(B,D),(C,D). Lowcast [D] stores the shortest one (B,D)

adjVex stores the vertex with the shortest path to other vertices in mst

For example, in the above example, the shortest vertex from each vertex to vertex D in mst is vertex B, so adjVex[D] stores vertex B

These three arrays are needed from the algorithm idea, and the specific implementation needs to be modified according to the actual code

/** Prim algorithm generates minimum spanning tree */
void PrimCreat(AdjList* adj)
{
    int min;        //Minimum weight
    int minIndex;   //Subscript of edge with minimum weight
    int isAdded[MAXSIZE] = {0};
    EdgeNode*  lowcost[MAXSIZE] = {NULL};                    //Save the edge information. If it is NULL, it means that the weight is infinite
    VertexNode* adjVex[MAXSIZE] = {NULL};                    //Save another vertex information Vi and Vadjvex[i], and the weight is lowcast [i]
    
    EdgeNode* temp = adj->VerNode[0]->firstEdge;    
    isAdded[0] = 1;
    for(int i = 0; i < adj->verQuantity; i++)               //Initialization of two arrays
    {
        adjVex[adj->VerNode[i]->id] = adj->VerNode[0];       //All point to the first vertex
        if(temp)
        {
            lowcost[temp->adjIndex] = temp;
            temp = temp->next;
        }
    }

    for(int i = 0; i < adj->verQuantity - 1; i++)
    {
        min = INFINITY;
        //First, find the edge with the smallest weight in lowcast and the corresponding non mst vertex subscript
        for(int k = 0; k < adj->verQuantity; k++)
        {
            if(lowcost[k] != NULL && lowcost[k]->weight < min)
            {
                min = lowcost[k]->weight;
                minIndex = k;
            }
        }
        //Print
        printf("(%d, %d)%d - ", adjVex[minIndex]->id, minIndex, min);

        isAdded[minIndex] = 1;
        //The vertex minIndex has been added to mst, and its distance from mst is 0 (there is no other state here, indicating that the distance is 0, which can only point to NULL)
        //If there is no isAdded array, it is impossible to distinguish whether NULL in lowcast means that the distance is 0 or infinity
        lowcost[minIndex] = NULL;

        //Update lowcast array
        //A new vertex is added to mst, and all updates are related to this vertex, so it is updated with all edges attached to this vertex
        temp = adj->VerNode[minIndex]->firstEdge;
        while(temp)
        {
            //Update is to find a shorter path, so the other vertex is not in mst and the weight is smaller
            if(isAdded[temp->adjIndex] != 1 && (lowcost[temp->adjIndex] == NULL || temp->weight < lowcost[temp->adjIndex]->weight))
            {
                lowcost[temp->adjIndex] = temp;
                adjVex[temp->adjIndex] = adj->VerNode[minIndex];    //Also update the adjVex array
            }
            temp = temp->next;
        }
    }
}

The specific ideas are written in the notes