I. Basic concepts

1. Standard Form of Linear Programming Problem

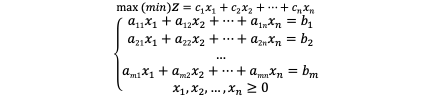
2. Simplex Method for Linear Programming (Table)

https://baike.baidu.com/item/simplex method/8580570?fr=aladdin

3. Artificial Variable Method

https://baike.baidu.com/item/artificial variable method/16629814?fr=aladdin
------------------

2. python Programming of Simplex Method

Step1: Establishing Simplex Table Classes

class Table(object):
    def __init__(self,X_num,B_num,z0,Xbase,bound):  #Initialization function
        self.X_num=X_num    #Number of variables
        self.B_num=B_num    #Number of constraints
        self.z0=z0          #objective function
        self.check=[]       #Inspection Number
        self.Xbase=Xbase    #Base variable
        self.bound=bound    #Constraints, including right-hand constants
        self.flag=0         #The type of solution, 0 is (temporarily) insoluble, 1 is the only optimal solution, 2 is the infinite number of optimal solutions.

Step2: Iterative Function

	def Iteration(self):    	#Iterative function
        lim=100		#Maximum number of iterations (to prevent infinite iterations without solutions)
        while(lim>0):
            self.check=[]
            for i in range(self.X_num):     #Calculate the number of tests
                temp=0
                for j in range(self.B_num):
                    temp+=self.bound[j][i]*self.z0[self.Xbase[j]]
                self.check.append(self.z0[i]-temp)
            self.IsEnd()		#Judging whether the iteration is over
            if self.flag>0:		#If there is a solution, the iteration ends.
                break
            else:				#Otherwise, base transformation is performed.
                self.BaseChange(1)
                lim-=1

Step3: Judging Iterative Termination Function

	def IsEnd(self):   	#Check whether the optimal solution is optimal and whether the optimal solution is unique
        self.flag=1
        zero=0
        for i in range(self.X_num):
            if self.check[i]>0:  #Non-optimal solution with test number greater than 0
                self.flag=0
                break
            if abs(self.check[i])<0.00001:   
            #Because M takes 1000, there is a slight error in the calculation of the test number.
                zero+=1
                if zero>self.B_num:
                    self.flag=2  
                    #The number of zeros in the test number is greater than the number of cardinal variables, and there are infinite optimal solutions.

Step4: Base Transform

    def BaseChange(self,model):   #Base transformation
        if model==1:
            [i,j,main]=self.FindMain()	#Simplex Method: Finding Main Elements
        else:
            [i,j,main]=self.FindMain2()	#Dual Simplex Method: Finding Main Elements
        self.Xbase[i]=j     #Replacement of base variables
        for t in range(self.X_num+1):	#Transform the row of the base variable
            self.bound[i][t]=self.bound[i][t]/main
        for k in range(self.B_num):		#Transform other rows
            if k!=i:
                times=self.bound[k][j]
                for t in range(self.X_num+1):
                    temp=self.bound[i][t]*times
                    self.bound[k][t]=self.bound[k][t]-temp

    def FindMain(self):    #Finding the Main Element
        j=self.check.index(max(self.check)) #Get the maximum value serial number in the number of tests
        theta=[]
        for i in range(self.B_num):
            if self.bound[i][j]==0:     #When the dividend is 0, give its theta a sufficiently large value
                th=1000
            else:
                th=self.bound[i][self.X_num]/self.bound[i][j]
            if th<0:                        #When theta < 0, give it a sufficiently large value
                th=10000
            theta.append(th)
        i=theta.index(min(theta))           #Get the minimum value serial number in the number of tests and replace it with
        main=self.bound[i][j]        
        return [i,j,main]