A

Title Description

There are \ (n \) non negative integers within \ ([0,2^w) \), you need to perform the following operations \ (n-1 \) times to minimize the remaining numbers:

• Select two nonnegative integers \ (x,y \) and combine them into one nonnegative integer \ (Z \), where \ (z=\lfloor\frac{(x|y)}{2}\rfloor \)
• Select a number \ (x \) to delete it.

\(n\leq 10^5,w\leq 60\)

solution

The first step can be divided into: \ (\ lfloor\frac{(x|y)}{2}\rfloor=\lfloor\frac{x}{2}\rfloor|\lfloor\frac{y}{2}\rfloor \), for problems with complex processes, you can consider guessing the conclusion in the direction of the result, like To make one Similarly to this question, let \ (d_i \) represent the number of times the last \ (I \) number is divided by two, then the final answer can be expressed as \ (\ frac {a_1} {2 ^ {d_1} | \ frac {a_2} {2 ^ {d_2}}... | \ frac {a_n} {2 ^ {d_n} \)

Considering the deletion operation, the necessary and sufficient conditions for a group of \ (\ {d \} \) to be legal are \ (\ sum {I = 1} ^ n \ frac {1} {2 ^ {d}} \ GEQ 1 \)

With this conclusion, let's consider from high to low. Assuming that the digit \ (w \) is considered now, we maintain \ (d_i \) for each number, and then consider changing the \ (w \) bit of the answer to \ (0 \) to see whether it is feasible. Now the answer to be verified is 11010 (0), Because of the or operation, we can't find that the answer is \ (0 \), but the corresponding bit after the number of \ (I \) is shifted to the right \ (d_i \) (we can judge directly by first or then XOR). We want to make \ (d_i \) as small as possible. It's illegal. We increase it step by step.

Time complexity \ (O(nw^2) \), but I'm very dissatisfied, so I can run freely.

#include <cstdio>
#include <cstring>
#include <iostream>
using namespace std;
const int M = 100005;
#define int long long
int read()
{
	int x=0,f=1;char c;
	while((c=getchar())<'0' || c>'9') {if(c=='-') f=-1;}
	while(c>='0' && c<='9') {x=(x<<3)+(x<<1)+(c^48);c=getchar();}
	return x*f;
}
int T,n,w,ans,a[M],d[M],td[M];
void work()
{
	n=read();w=read();
	for(int i=1;i<=n;i++)
		a[i]=read();
	ans=(1ll<<w)-1;
	memset(d,0,sizeof d);
	for(int t=w-1;t>=0;t--)
	{
		int now=ans^(1ll<<t),sum=0;
		for(int i=1;i<=n;i++)
		{
			td[i]=d[i];
			while(((a[i]>>d[i])|now)^now) d[i]++;
			sum+=(1ll<<w-d[i]);
			if(sum>=(1ll<<w)) break; 
		}
		if(sum>=(1ll<<w)) ans=now;
		else memcpy(d,td,sizeof td);
	}
	printf("%lld\n",ans);
}
signed main()
{
	freopen("merge.in","r",stdin);
	freopen("merge.out","w",stdout);
	T=read();
	while(T--) work();
}

B

Title Description

For the string \ (t \), define a line walk and select a positive integer sequence \ (t_1,t_2...t_m \) of any length, where \ (\ forall i\in[1,m],t_i\in [1,|T|],|t_i-t_{i-1}|=1,t_1\not=t_m \) is a palindrome string.

It is good to call a string if and only if each position of the string can be passed at least once through several walks. Now there are \ (q \) times to ask whether it is good to ask a substring \ (s[l_i...r_i] \) each time.

\(n,q\leq 10^6\)

solution

We can find that if there is A small odd palindrome string such as ABA, there must be A solution. This is because accessing all points from one point and then returning to this point can form A palindrome string, but it does not meet the restrictions of different subscripts at the beginning and end. In this case, we can finally go to another A to get the solution.

The problem now is to investigate whether the even palindrome string can cover a complete interval. We consider decomposing this restriction to each position. Let's assume that the nearest symmetric point to the left of a point is \ (l_i \) and the nearest symmetric point to the right is \ (r_i \). I will further explain it with the following figure:

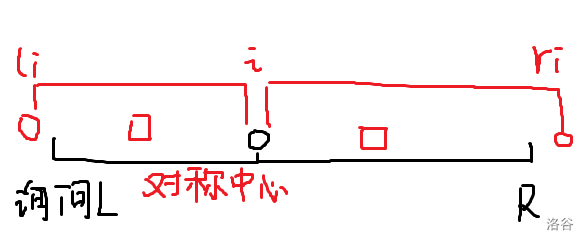
The above figure shows the illegal point \ (I \), so the necessary and sufficient condition that a query cannot be covered by the even palindrome string is \ (\ exist i\in[L,R],[L,R]\subseteq (l_i,r_i) \), in which \ (l_i,r_i \) can be simply preprocessed with the binary hash \ (\) segment tree at the beginning. In particular, if the left side does not cover its symmetry center, then \ (l_i=0 \), If the right side does not cover its center of symmetry, then \ (r_i=n+1 \)

Then the rest is a partial order problem. We consider making scanning lines in the order of the left end points. The scanning process is as follows:

• Add all \ (l_i < L \) so that we solve a quarter of the partial order relationship.
• If the right endpoint falls in \ ([I, r_, I) \), it must be illegal, then we mark it illegal in this interval.
• Finally, we need to solve \ (i\geq L \), so we need to delete the point of \ (I < L \) before querying.

Then the time complexity \ (O(n\log n) \), simple pointer and tree array can be used.

#include <cstdio>
#include <iostream>
#include <algorithm>
#include <set>
using namespace std;
const int M = 1000005;
#define pii pair<int,int>
#define ull unsigned long long
int read()
{
	int x=0,f=1;char c;
	while((c=getchar())<'0' || c>'9') {if(c=='-') f=-1;}
	while(c>='0' && c<='9') {x=(x<<3)+(x<<1)+(c^48);c=getchar();}
	return x*f;
}
int n,m,a[M],b[M],id[M],ans[M],mx[M<<2],mi[M<<2];
ull pw[M],hs[M][2];char s[M];multiset<pii> z;
struct node
{
	int l,r,id;
	bool operator < (const node &b) const
		{return l<b.l;}
}h[M],q[M];
//segment tree
ull check(int l,int r,int op)
{
	if(op==0) return hs[r][0]-hs[l-1][0]*pw[r-l+1];
	return hs[l][1]-hs[r+1][1]*pw[r-l+1];
}
void updmax(int i,int l,int r,int L,int R,int c)
{
	if(L>r || l>R) return ;
	if(L<=l && r<=R) {mx[i]=max(mx[i],c);return ;}
	int mid=(l+r)>>1;
	updmax(i<<1,l,mid,L,R,c);
	updmax(i<<1|1,mid+1,r,L,R,c);
}
void updmin(int i,int l,int r,int L,int R,int c)
{
	if(L>r || l>R) return ;
	if(L<=l && r<=R) {mi[i]=min(mi[i],c);return ;}
	int mid=(l+r)>>1;
	updmin(i<<1,l,mid,L,R,c);
	updmin(i<<1|1,mid+1,r,L,R,c);
}
void dfs(int i,int l,int r)
{
	if(l==r) {id[l]=i;return ;}
	int mid=(l+r)>>1;
	mx[i<<1]=max(mx[i<<1],mx[i]);
	mx[i<<1|1]=max(mx[i<<1|1],mx[i]);
	mi[i<<1]=min(mi[i<<1],mi[i]);
	mi[i<<1|1]=min(mi[i<<1|1],mi[i]);
	dfs(i<<1,l,mid);
	dfs(i<<1|1,mid+1,r);
}
void init()
{
	pw[0]=1;
	for(int i=1;i<=n;i++)
	{
		if(i+2<=n && s[i]==s[i+2]) a[i]++;
		pw[i]=pw[i-1]*371;a[i]+=a[i-1]; 
		hs[i][0]=hs[i-1][0]*371+s[i];
	}
	for(int i=n;i>=1;i--)
		hs[i][1]=hs[i+1][1]*371+s[i];
	for(int i=1;i<=4*n;i++) mi[i]=n+1;
	for(int i=1;i<n;i++)
	{
		int l=1,r=min(i,n-i),len=0;
		while(l<=r)
		{
			int mid=(l+r)>>1;
			if(check(i-mid+1,i,0)==check(i+1,i+mid,1))
				len=mid,l=mid+1;
			else r=mid-1;
		}
		if(len)
			updmax(1,1,n,i+1,i+len,i+1),
			updmin(1,1,n,i-len+1,i,i);
	}
	dfs(1,1,n);
	for(int i=1;i<=n;i++)
	{
		int t1=mx[id[i]],t2=mi[id[i]];
		h[i]=node{!t1?0:2*t1-i-1,t2>n?n+1:2*t2-i+1,i};
	}
}
//tree-array
int lowbit(int x)
{
	return x&(-x);
}
void add(int x,int c)
{
	for(int i=x;i<=n;i+=lowbit(i))
		b[i]+=c;
}
int ask(int x)
{
	int r=0;
	for(int i=x;i>0;i-=lowbit(i))
		r+=b[i];
	return r;
}
signed main()
{
	freopen("pass.in","r",stdin);
	freopen("pass.out","w",stdout);
	n=read();scanf("%s",s+1);
	init();m=read();
	for(int i=1;i<=m;i++)
	{
		q[i].l=read(),q[i].r=read(),q[i].id=i;
		if(q[i].r>2) ans[i]|=(a[q[i].r-2]-a[q[i].l-1]>0);
	}
	sort(h+1,h+1+n);sort(q+1,q+1+m);
	for(int i=1,j=1;i<=m;i++)
	{
		while(j<=n && h[j].l<q[i].l)
		{
			add(h[j].id,1);add(h[j].r,-1);
			z.insert(make_pair(h[j].id,h[j].r));
			j++;
		}
		while(!z.empty() && z.begin()->first<q[i].l)
		{
			pii t=*z.begin();z.erase(z.begin());
			add(t.first,-1);add(t.second,1);
		}
		ans[q[i].id]|=(ask(q[i].r)==0);
	}
	for(int i=1;i<=m;i++)
		putchar(ans[i]+'0');
}