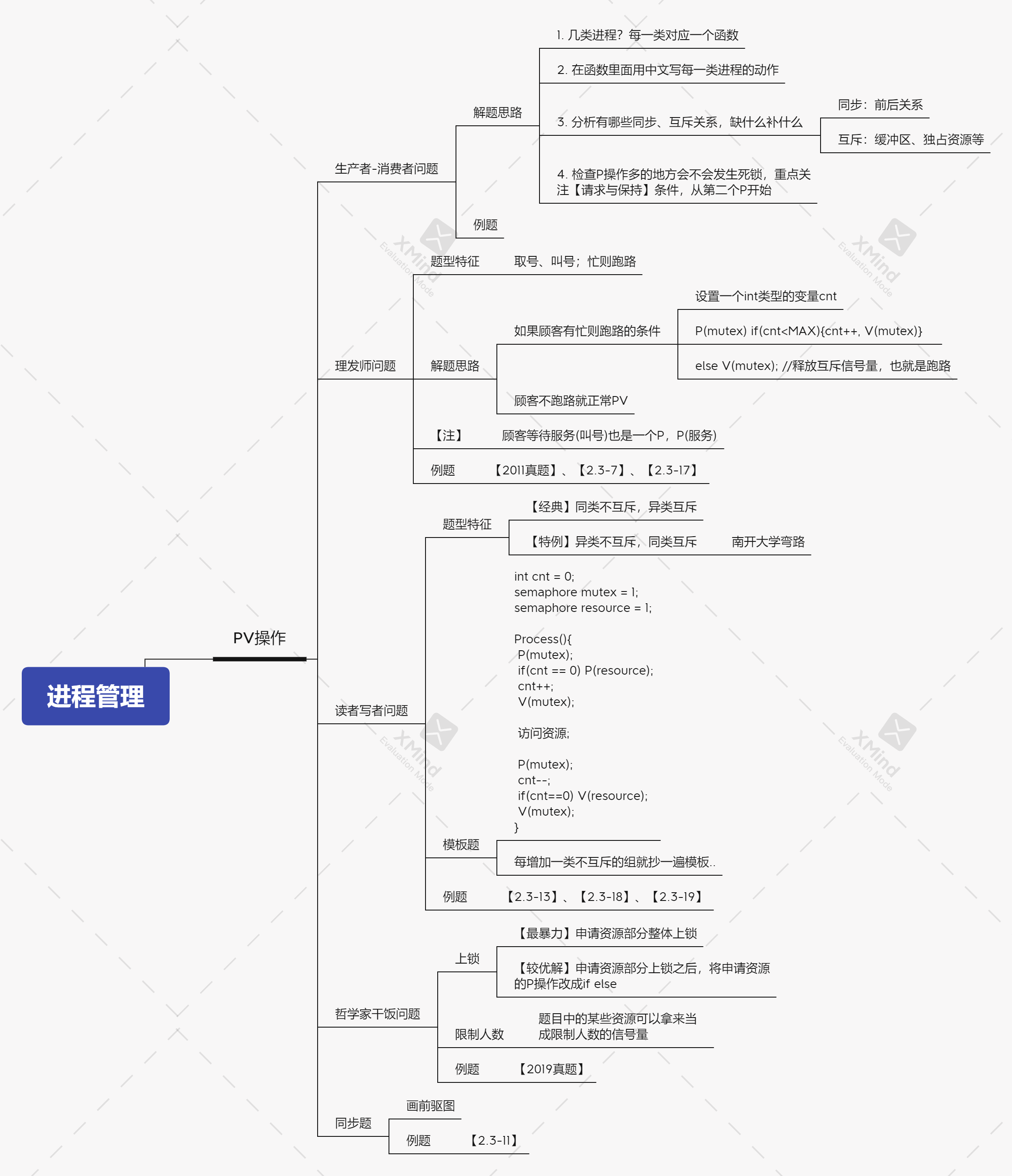
PV operation questions

PV operation knowledge structure

the dining philosophers problem

Problem Description:

Have n (n) ≥ \ge ≥ 3) philosophers sit around a round table, and each philosopher eats and thinks alternately. There is m(m) in the center of the round table ≥ \ge ≥ 1) bowl, with one chopstick between each two philosophers. Every philosopher must take a bowl and chopsticks on both sides before eating. After eating, put the bowl and chopsticks back in place and continue thinking. In order to make as many philosophers eat at the same time as possible and prevent deadlock, please use the P and V operations of semaphores [wait(), signal() operation] to describe the mutual exclusion and synchronization in the above process, and explain the meaning of semaphores and initial values used.

Solution 1: limit the maximum number of people who can access resources

semaphore capacity = n-1;		//Indicates that at most n-1 philosophers can compete for resources
semaphore bowl = m;				//bowl
semaphore chopsticks[n] = {1};	//n chopsticks,
for(int i = 0; i < n; i++)
	chopsticks[i] = 1;			//The number of chopsticks on each side is 1

Process Philosopher()
{
	while(true)
	{
		reflection
		
		P(capacity);			//Up to n-1 people can access the resource
		P(bowl)					//Application bowl
		P(chopsticks[i]);		//Left hand chopsticks
		P(chopsticks[(i+1)%n]	//Right hand chopsticks
		Dry rice
		V(bowl);
		V(chopsticks[i]);
		V(chopsticks[(i+1)%n];
		V(capacity);
		
	}
}

Solution 1 Optimization

The number of bowls m can be used to limit the number of visitors, that is, the semaphore bowl not only acts as a resource, but also limits the number of visitors. It should be noted that the number of bowls must be less than n

semaphore bowl；				//bowl
semaphore chopsticks[n] = {1};	//n chopsticks,
for(int i = 0; i < n; i++)
	chopsticks[i] = 1;			//The number of chopsticks on each side is 1
bowl = min(m,n-1);				//Limit the maximum number of people accessing resources to n-1

Process Philosopher()
{
	while(true)
	{
		reflection
		
		P(bowl);				//Take a bowl
		P(chopsticks[i]);		//Left hand chopsticks
		P(chopsticks[(i+1)%n]	//Right hand chopsticks
		
		Dry rice
		
		V(chopsticks[i]);
		V(chopsticks[(i+1)%n];
		V(bowl);
	}
}

Solution 2: mutually exclusive access to resources (locking)

Book Description: a philosopher is allowed to grab chopsticks only when both left and right chopsticks are available.

Personal understanding: in fact, this strategy is to "lock" the whole process of philosophers applying for resources, that is, when philosophers can only apply for resources mutually exclusive, it ensures that the first philosopher can apply for all resources.

semaphore lock = 1;				//Semaphores used to mutually exclusive request resources
semaphore bowl = m；			//bowl
semaphore chopsticks[n] = {1};	//n chopsticks,
for(int i = 0; i < n; i++)
	chopsticks[i] = 1;			//The number of chopsticks on each side is 1

Process Philosopher()
{
	while(true)
	{
		reflection
		
		P(lock);				//"Lock"
		P(chopsticks[i]);		//Left hand chopsticks
		P(chopsticks[(i+1)%n]	//Right hand chopsticks
		P(bowl);				//Take a bowl
		V(lock);
		
		Dry rice
		
		V(chopsticks[i]);
		V(chopsticks[(i+1)%n];
		V(bowl);
	}
}

Solution two optimization

In the previous solution, if the process scheduling occurs after the processes of philosophers other than the first philosopher execute the application, and after one cycle of concurrent execution, There will be a situation that only the first philosopher has the resources to eat in his hand (at worst), while other philosophers only have a chopstick in his left hand. This is consistent with the requirement of "Let as many philosophers eat at the same time" Inconsistent. Therefore, consider the following optimization. While locking, judge whether philosophers can apply for all resources. If they can, take them. Otherwise, they will not apply.

int n = 10;                         //Number of chopsticks
 int m = 10;                        //Number of bowls
semaphore lck = 1;					//Semaphore of resource
bool chopsticks[n];            		//The status of all chopsticks, false is not taken away
int bowls = 0;                     	//Number of bowls currently allocated
for(int i = 0; i < n; i++)
	chopsticks[i] = false;			//Initialize all chopsticks as not taken away

Progress Philosopher(int i)			//Philosopher i
{
    while (true)
    {
    	//reflection
    	
        P(lck);		//Ensure that only one philosopher is trying to take it at the same time
        if (!chopsticks[i] && !chopsticks[(i + 1) % n] && bowls < m)//Only when you can get all the resources can you apply
        {
            chopsticks[i] = true;           //Take the left chopsticks
            chopsticks[(i + 1) % n] = true; //Take your right chopsticks
            bowls++;                        //Take a bowl
        }
        V(lck);

        //Dry rice

        P(lck);                             //Mutually exclusive access array
        chopsticks[i] = false;              //Put down your left chopsticks
        chopsticks[(i + 1) % n] = false;    //Put down your right chopsticks
        bowls--;                            //Release bowl
        V(lck);
    }
}