1.reshape

reshape is reshaping. Three commonly used expressions are as follows:

numpy.arange(n).reshape(a, b)    
# n natural numbers are generated in turn and displayed in the form of an array of rows a and columns b

numpy.arange(a,b,c)    
# Starting from the number a, the step is c, and ending at b, the array is generated

numpy.arange(a,b,c).reshape(m,n) 
# Change the dimension of array into m rows and n columns.

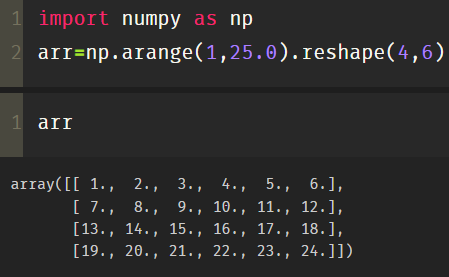
Example 1:

import numpy as np
arr=np.arange(1,25.0).reshape(4,6)

About order:
order can be an array with different sorting directions
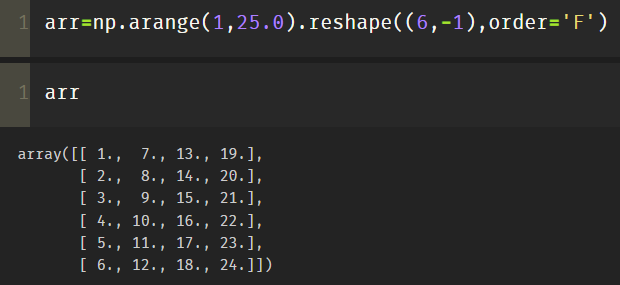
(1) order='F 'column is the main order
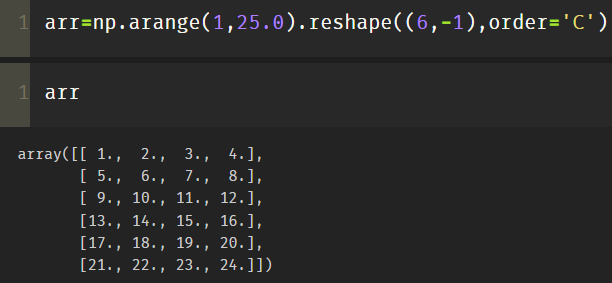
(2) order='C 'behavior main order

One is to sort the array vertically by order='F ':

arr=np.arange(1,25.0).reshape((6,-1),order='F')

One is to sort the array horizontally by order='C ':

arr=np.arange(1,25.0).reshape((6,-1),order='C')

reshape and flattern:
The former completes the transformation from low dimension to high dimension, while the latter, on the contrary, can also use the reval function

2.flatten

numpy.ndarray.flattern() is a function that returns a one-dimensional array.
You can also use order like reshape

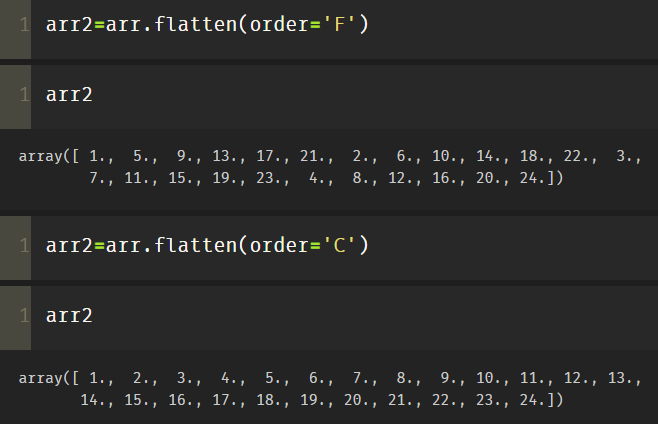
arr2=arr.flatten(order='F')

Generally, order='C 'is used by default. If there are specific requirements, order='F' is used.

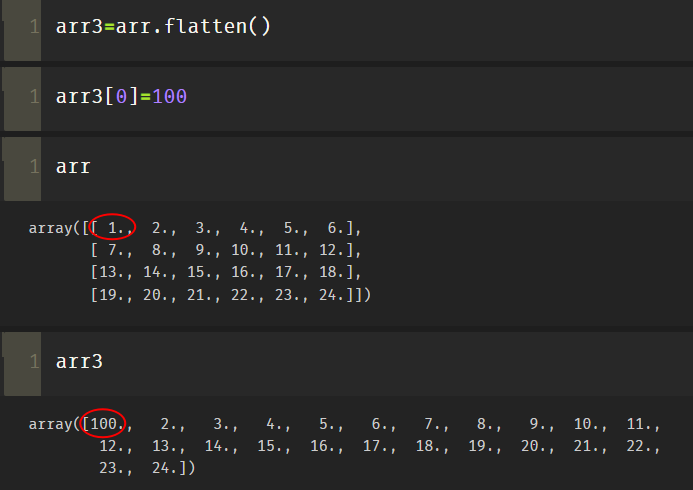
And flatten() returns a copy, which means that changing the value of the element will not affect the original array.

3.ravel

The travel () method pulls the array dimension into a one-dimensional array

Difference between t ravel and flatten:

1. T ravel does not copy the original array when flattening, but only copies the original array when the column main order is leveled
2. flatten copied the original array in all cases
3. Travel () returns the view, which means that changing the value of the element will affect the original array;
4. flatten() returns a copy, meaning that changing the value of an element will not affect the original array.
5. The same point: the function of these two functions is to convert multi-dimensional arrays into one-dimensional arrays

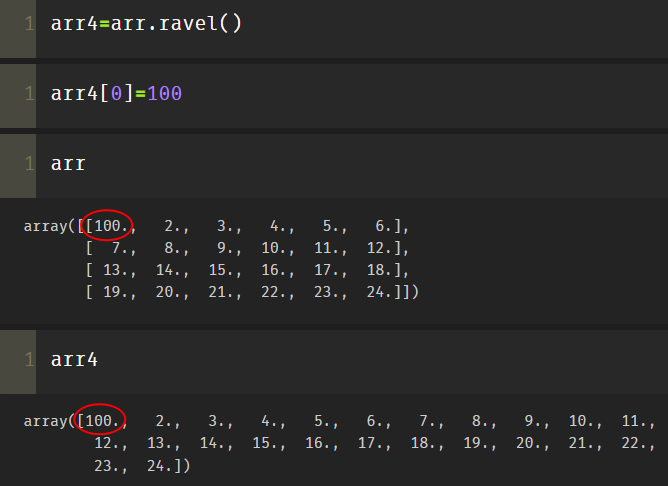
Travel () returns the view, which means that changing the value of the element will affect the original array;

4.stack

numpy.stack(arrays, axis=0): a sequence of arrays connected along a new axis.

A series of stack functions are: stack(), hstack(), vstack()

(1)concatenate

There are also attributes, such as concatenate
numpy.concatenate((a1,a2,...), axis=0) function can complete the splicing of multiple arrays at one time. Where a1,a2,... Are parameters of array type

arr1=['Hug you through the cold winter','Anti corruption storm 5: final chapter','Li Mao plays Prince','Manslaughter 2']
arr2=['Love in years','Love myth','Matrix restart','Lion boy']
np.concatenate([arr1,arr2])

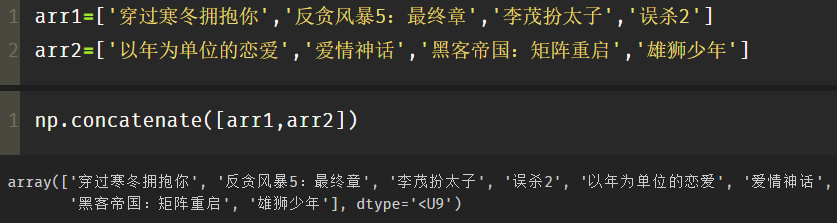
Note that you need to use [] when merging two list s, otherwise an error will occur.


The axis parameter specifies the index of the new axis in the resulting size. For example, if axis=0, it will be the first dimension, and if axis=-1, it will be the last dimension.

By default, axis=0

arr1=np.arange(1,25.0).reshape(4,6)
arr2=np.arange(26,50.0).reshape(4,6)
np.concatenate([arr1,arr2],axis=1)
np.concatenate([arr1,arr2],axis=0)

As shown in the above figure, axis=1 concatenates different columns, and axis=0 is similar to append, which is a merge.

Swap arr1 and arr2:

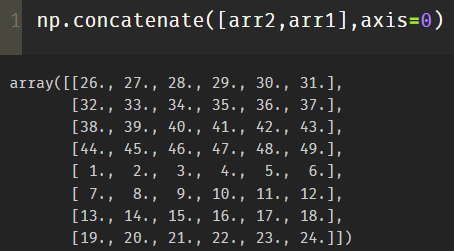
(2)vstack

Function prototype: vstack(tup). The parameter tup can be tuple, list, or numpy array, and the returned result is numpy array. It stacks arrays vertically (in row order).

vstack and concatenate(), axis = 0 are equivalent

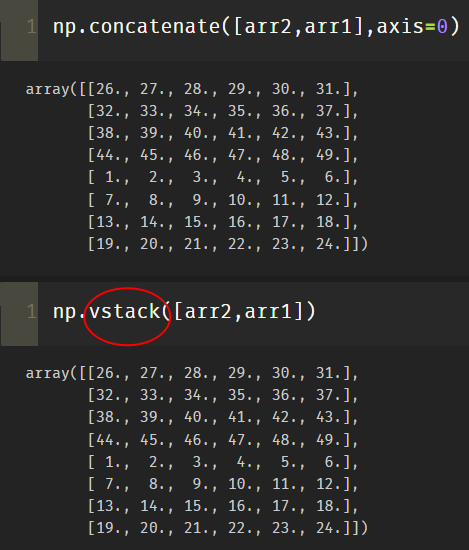
(3)dstack

dstack is a deep stack, that is, merging in the depth direction.

dstack can change a one-dimensional array into a three-dimensional array.

import numpy as np

# vstack
np.vstack([arr1,arr2])
#result:
array([[ 1.,  2.,  3.,  4.,  5.,  6.],
       [ 7.,  8.,  9., 10., 11., 12.],
       [13., 14., 15., 16., 17., 18.],
       [19., 20., 21., 22., 23., 24.],
       [26., 27., 28., 29., 30., 31.],
       [32., 33., 34., 35., 36., 37.],
       [38., 39., 40., 41., 42., 43.],
       [44., 45., 46., 47., 48., 49.]])
       
# dstack
np.dstack([arr1,arr2])
# result:
array([[[ 1., 26.],
        [ 2., 27.],
        [ 3., 28.],
        [ 4., 29.],
        [ 5., 30.],
        [ 6., 31.]],

       [[ 7., 32.],
        [ 8., 33.],
        [ 9., 34.],
        [10., 35.],
        [11., 36.],
        [12., 37.]],

       [[13., 38.],
        [14., 39.],
        [15., 40.],
        [16., 41.],
        [17., 42.],
        [18., 43.]],

       [[19., 44.],
        [20., 45.],
        [21., 46.],
        [22., 47.],
        [23., 48.],
        [24., 49.]]])

(4)hstack

Function prototype: hstack(tup). The parameter tup can be a tuple, a list, or a numpy array. The array with the return result of numpy is stacked horizontally (in column order). The vstack() function is just the opposite.

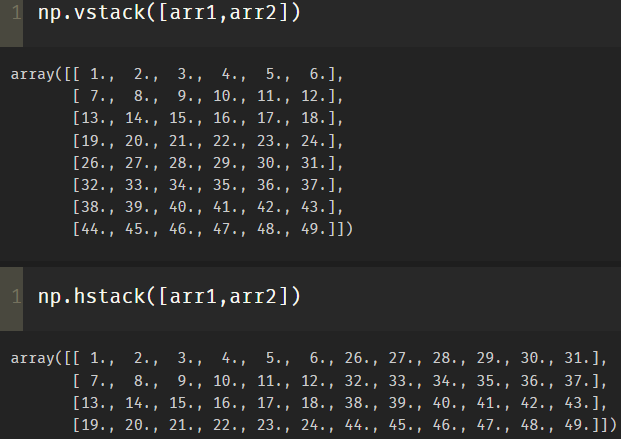
(5) r,c mode

np.r_[arr1,arr2] is actually a concatenate between vstack and axis=0.
np.c_[arr1,arr2], hstack combines with axis=1.

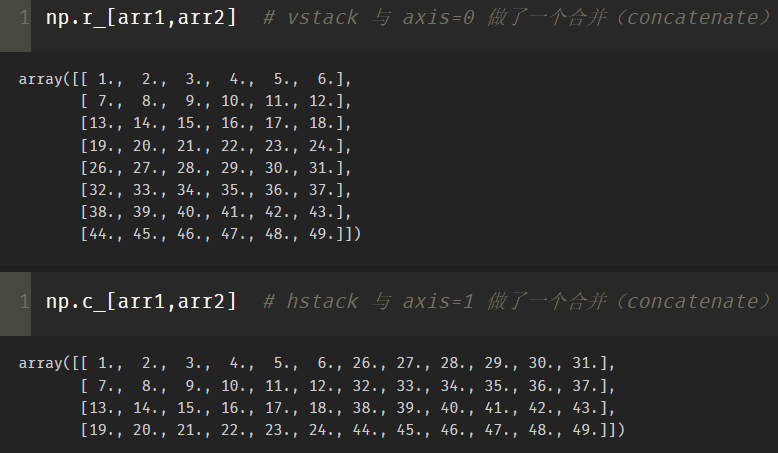
print(np.r_[-2:2:1,[0]*3,5,6])

The above code consists of three parts, - 2:2:1 represents numbers from - 2 to 2, with an interval of 1 and no 2, then three zeros, followed by 5 and 6

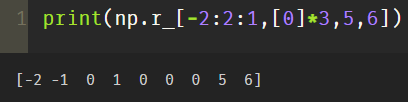
print((np.r_['r',-2:2:1,[0]*3,5,6])) #Two dimensional array, rendered in rows
print((np.r_['c',-2:2:1,[0]*3,5,6])) #Two dimensional array, presented as columns

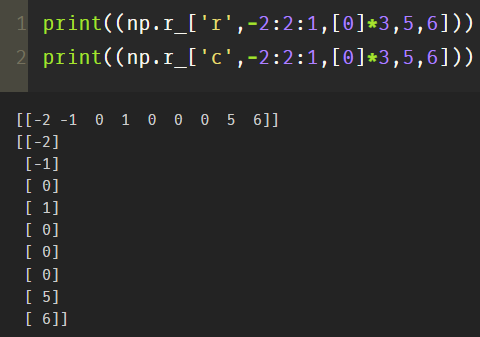
The default is r, which means it is created in the direction of row, and c means it is created in the form of column.

Note: shape represents the dimension size of the matrix.

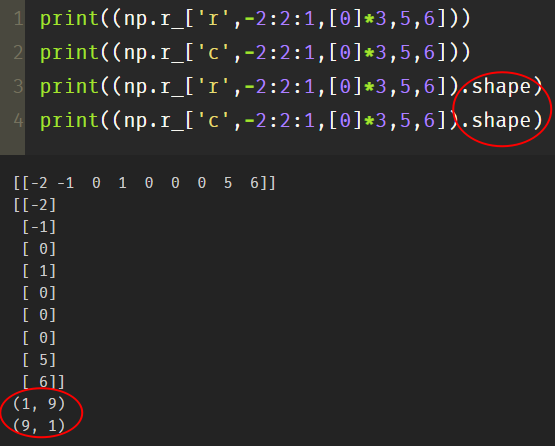
It can also be represented by 'a,b,c'. A represents the axis. Merging along axis a represents that the array dimension after merging is at least b, and c represents dimension promotion on dimension c

print(np.r_['0,2,0',[1,2,3],[4,5,6]],'\n')
print(np.r_['0,2,1',[1,2,3],[4,5,6]],'\n')
print(np.r_['1,2,0',[1,2,3],[4,5,6]],'\n')
print(np.r_['1,2,1',[1,2,3],[4,5,6]])

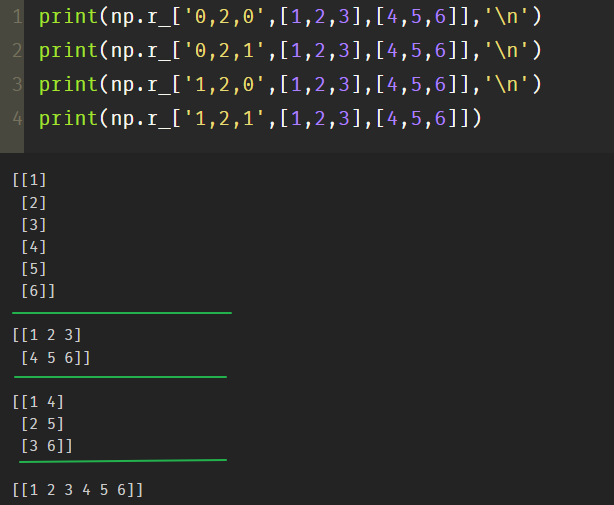
 b:Dimensions of the merged array
 a=0,Merge along axis 0.(3,)-->(1,3)
 a=1,Merge along axis 1.(3,1)-->(3,2)
 c=0,Rise one dimension on axis 0,(3,)-->(3,1)
 c=1,One dimensional rise on axis 1,(3,)-->(1,3)

5.split

(1)split

Split includes split(), hsplit(), vsplit()

arr1=np.arange(1,13.0).reshape(2,6)
arr2=np.arange(14,26.0).reshape(2,6)
arr=np.concatenate([arr1,arr2])
arr3=np.split(arr,2)   # By default, axis=0

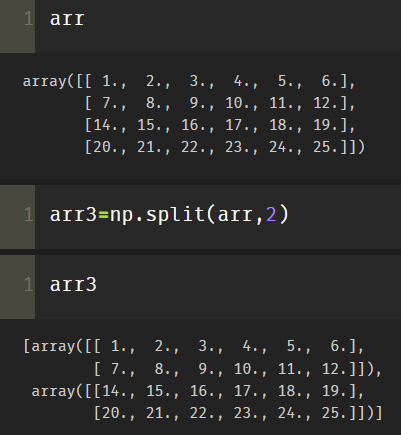
As can be seen from the above figure, split is divided into two-dimensional arrays

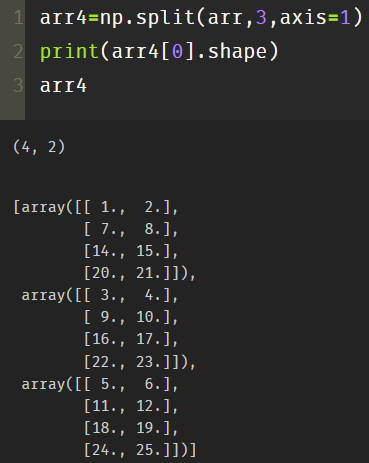
arr4=np.split(arr,3,axis=1)
print(arr4[0].shape)
arr4

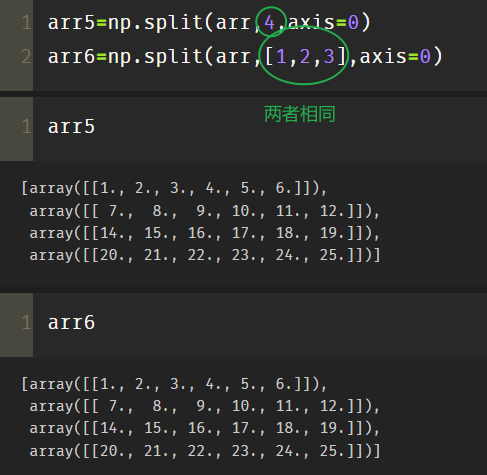
arr5=np.split(arr,4,axis=0)
arr6=np.split(arr,[1,2,3],axis=0)

The two lines of the above code block are the same, and the second line is equivalent to using the slicing method of array.

(2) vsplit and hsplit

1. Split vsplit into multiple vertical arrays.
2. hsplit splits the array horizontally (by column) into multiple sub arrays.

I hope you can see the following figure in this part~

arrv=np.vsplit(arr,[1,2,3,4])
arrh=np.hsplit(arr,[1,2,3,4,5])

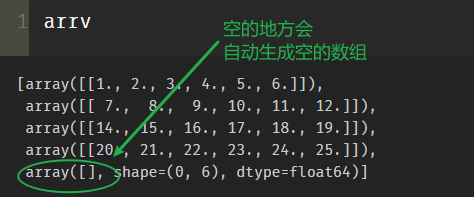
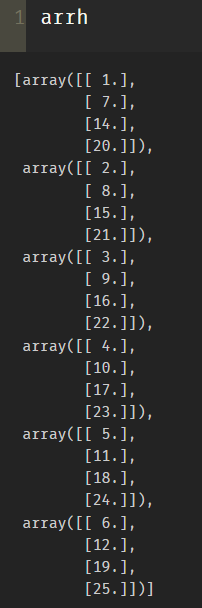
6.repeat

repeat(): copies each specified element in the array.
One dimensional array: use integer and list references to control the number of copied elements
Multidimensional array: use integer type and list type to control the number of copied elements

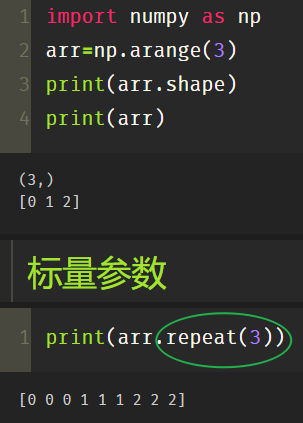
import numpy as np
arr=np.arange(3)
print(arr.shape)

(1) Scalar parameter

print(arr.repeat(3))   # Each element is copied three times

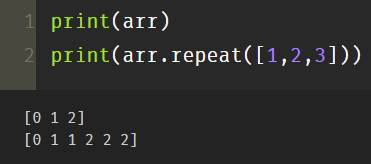
(2) List parameters

print(arr)
print(arr.repeat([1,2,3]))  
# The first one is not copied, the second one is copied, and so on

When the elements of the list are less than array elements or redundant array elements, an error will be reported, as shown in the following figure.

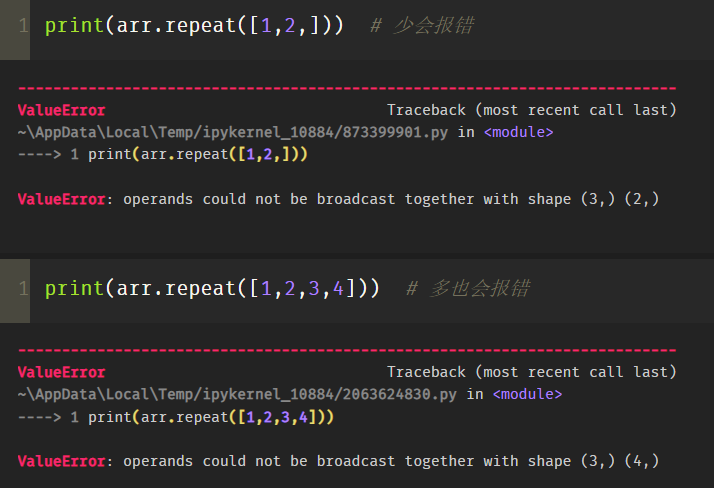
The above is the of one-dimensional array. Next, let's look at the scalar parameters and axis parameters used in two-dimensional array:

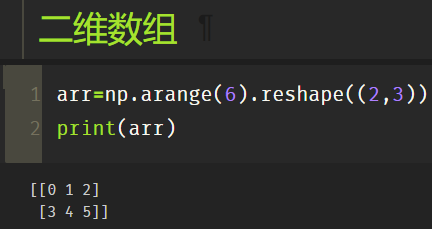
print(arr.repeat(2)) # At this point, the two-dimensional array becomes one-dimensional
print(arr.repeat(2,1)) 
print(arr.repeat(2,axis=0)) # Copy on line

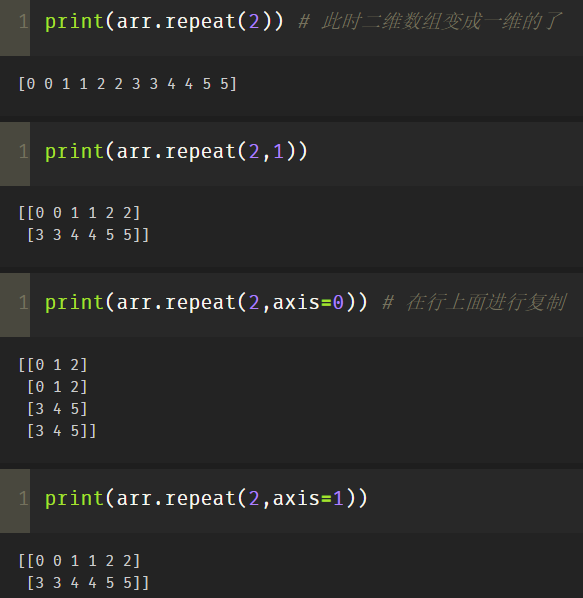
Let's take another look at the list parameters and axis parameters in the two-dimensional array:

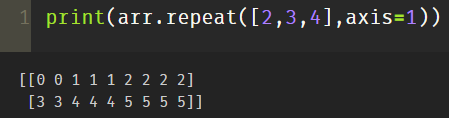
7.tile

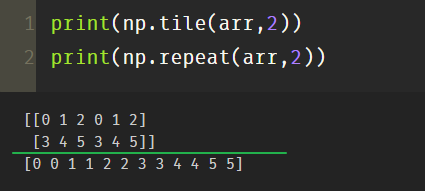
As for repeat and title, the essence of both is replication, while repeat is assigned at the element level and title is assigned at the array level.

(1) Scalar parameter

print(np.tile(arr,2))
print(np.repeat(arr,2))

(2) Tuple parameters

Tuple parameters are divided by relevant parameters in parentheses.

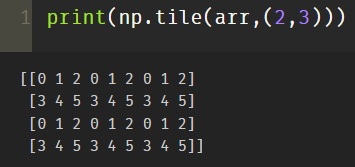
print(np.tile(arr,(2,3)))

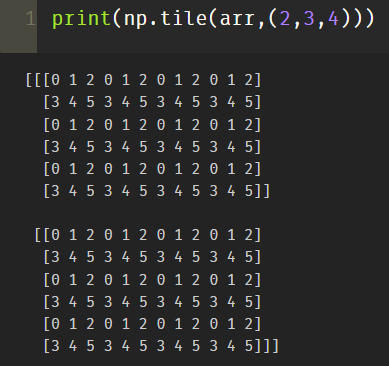
print(np.tile(arr,(2,3,4)))

Copy the axis 0 twice, the row 3 times and the column 4 times.

8.sort

Sorting is divided into:

1. Direct sort
2. Indirect sorting

Direct sort(): sort on the original array without re creating an array

(1) One dimensional array sorting method

arr=np.array([9,1,5,7,2,3,8,6]) # First create an unordered array
arr

print('Array before sorting:',arr)
arr.sort()
print('Sorted array:',arr)

arr[::-1] # Display in reverse order

(2) Multidimensional array sorting method

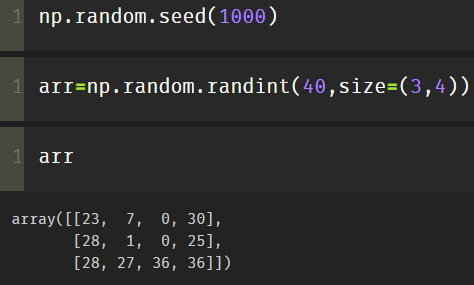
First use random to randomly generate a two-dimensional array: (each time)

import numpy as np
np.random.seed(1000)
arr=np.random.randint(40,size=(3,4))
arr

The above method will change the number of the array after each refresh.

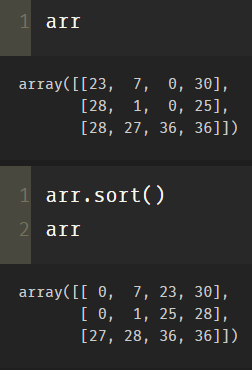
If you use arr.sort() directly for a two-dimensional array, the rows will be sorted directly.

Sort columns:

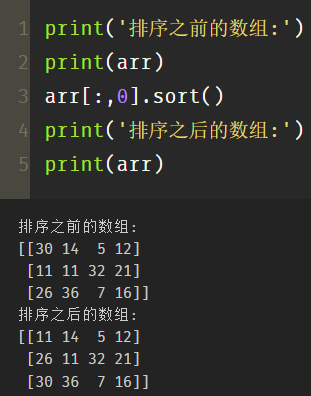
print('Array before sorting:')
print(arr)
arr[:,0].sort()
print('Sorted array:')
print(arr)

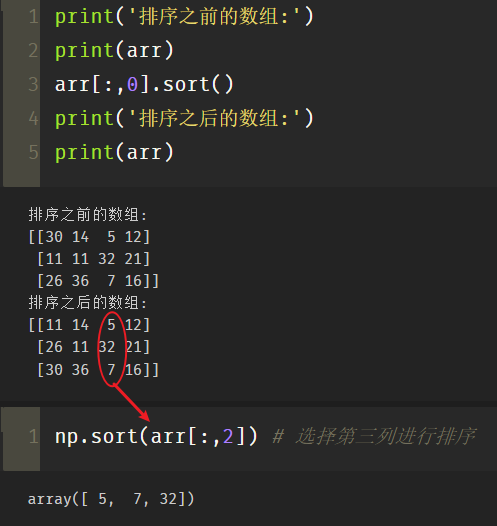
np.sort(arr[:,2]) # Select the third column to sort

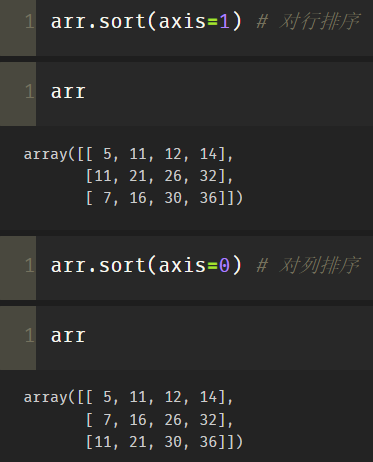
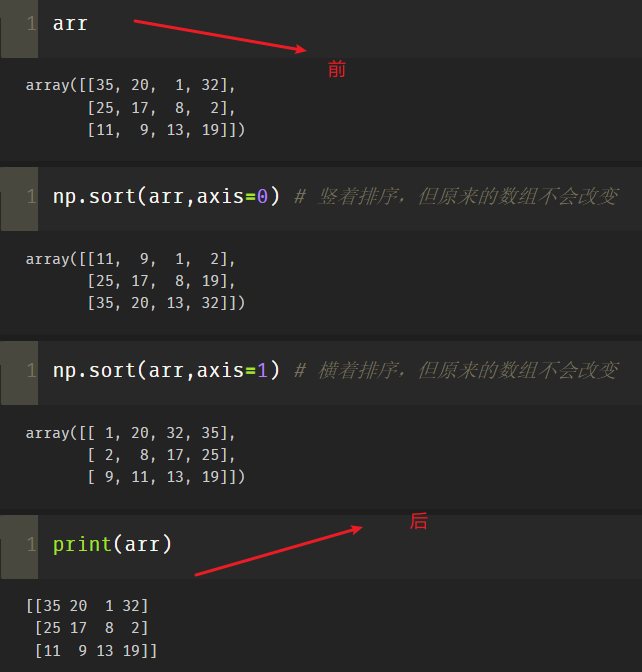
arr.sort(axis=1) # Sort horizontally, and the original array changes
np.sort(arr,axis=1) # Sort horizontally, but the original array will not change
arr.sort(axis=0) # Sort vertically, and the original array changes
np.sort(arr,axis=0) # Sort vertically, but the original array will not change

(3) argsort function

Next, look at indirect sorting:

Indirect sort: sort by using specific parameters and sort on demand. argsort() function is required
argsort function: returns the index value of the array value from small to large.

score=np.array([100,65,76,89,58])
idx=score.argsort()
idx

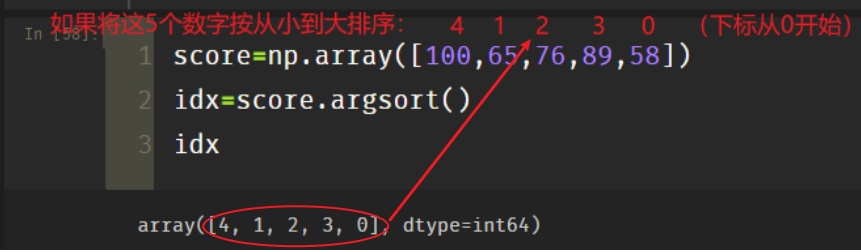
Therefore, if you print the array with superscript and subscript, it is equivalent to sorting:

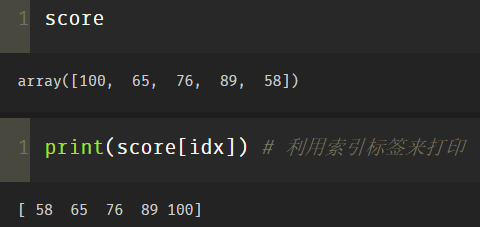
print(score[idx]) # Print with index labels

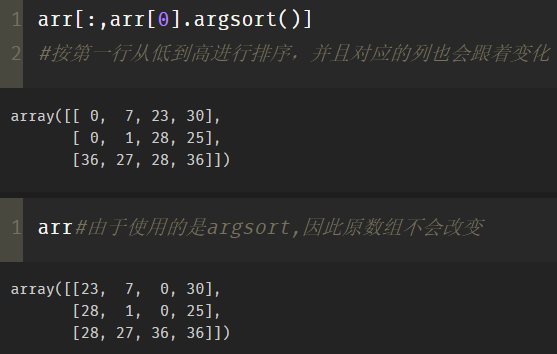
arr[:,arr[0].argsort()]
#Sort by the first row from low to high, and the corresponding columns will change accordingly 
arr#Since argsort is used, the original array will not change 

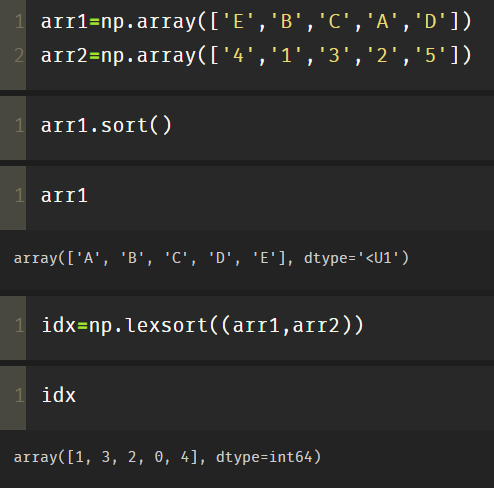
(4) Lexport function

numpy. Lexport () is used to sort multiple sequences. Think of it as a sort of spreadsheet, with each column representing a sequence, giving priority to the next column.

Here is an application scenario: in the junior high school entrance examination, students admitted to key classes are admitted according to the total score. If the total score is the same, those with high math scores will be admitted first. If the total score and math scores are the same, they will be admitted according to the English score... Here, the total score is in the last column of the spreadsheet, the math score is in the penultimate column, and the English score is in the penultimate column.

arr1=np.array(['E','B','C','A','D'])
arr2=np.array(['4','1','3','2','5'])
idx=np.lexsort((arr1,arr2))

9.insert

Insert is an insert, but the original array will not change.

arr=np.arange(6)
np.insert(arr,1,100) # Insert 100 at subscript 1

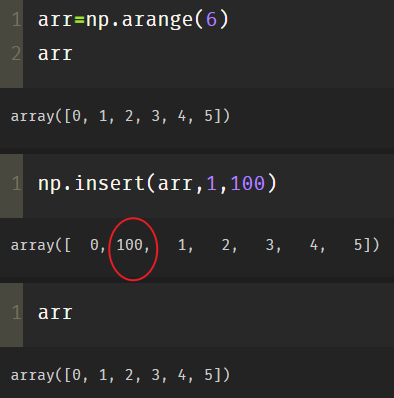
arr1=np.insert(arr,1,100)
arr1  

10.delete

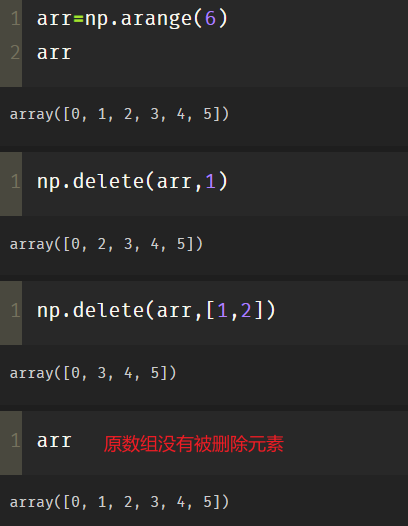
Delete is to delete, but the original array will not change.

arr=np.arange(6)
np.delete(arr,1)
np.delete(arr,[1,2])

11.copy

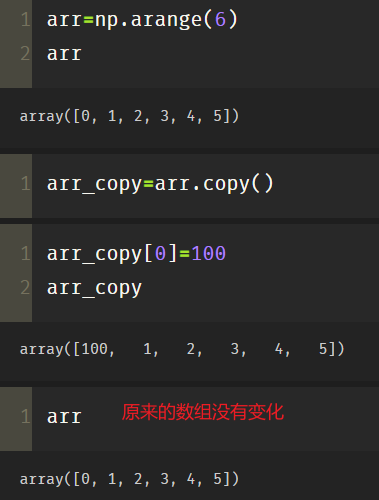
About copy and view, here we need to know the difference between array slice and list slice:

1. The array slice gets a view of the original array. Modifying the contents of the slice will change the original array
2. The list slicing obtains a copy of the original list. The list after modifying the slicing will not change the original list

arr=np.arange(6)
arr_copy=arr.copy()
arr_copy[0]=100
arr_copy

12.view

arr=np.arange(6)
arr_view=arr.view()
arr_view[0]=100
arr_view

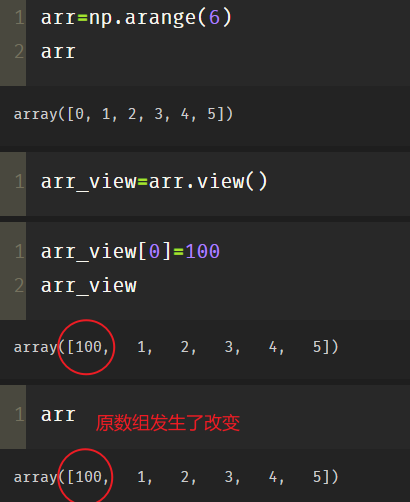
After talking about the above 12 array deformations, how to use the characteristics of container data and the methods of array related functions to de duplicate strings or other objects?

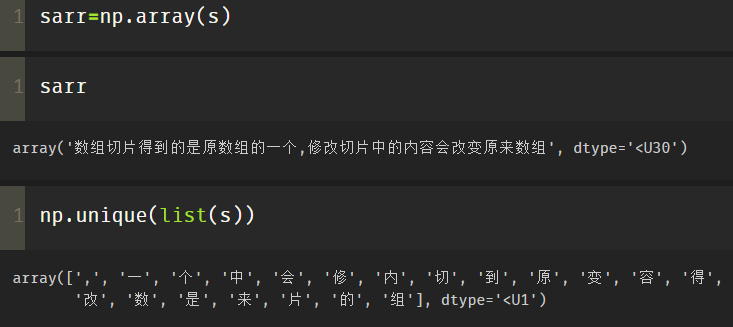
s='Array slicing gets a copy of the original array,Modifying the contents of the slice will change the original array'

Suppose you want to de duplicate s now:

Method 1: use set

sets=set(s)

Method 2: use unique

sarr=np.array(s)
np.unique(list(s))