Data structures and algorithms (Python)

1. Introduction of concepts

If a+b+c=1000 and a2+b2=c^2 (a, b and c are natural numbers), how to find all possible combinations of a, b and c?

Enumeration method:

First attempt

import time
start_time = time.time()

# Note that it is a triple cycle
for a in range(0, 1001):
    for b in range(0, 1001):
        for c in range(0, 1001):
            if a**2 + b**2 == c**2 and a+b+c == 1000:
                print("a, b, c: %d, %d, %d" % (a, b, c))

end_time = time.time()
print("elapsed: %f" % (end_time - start_time))
print("complete!")

Operation results:

a, b, c: 0, 500, 500
a, b, c: 200, 375, 425
a, b, c: 375, 200, 425
a, b, c: 500, 0, 500
elapsed: 214.583347
complete!

It took 214.583347 seconds.

Concept of algorithm

Algorithm is the essence of computer processing information, because computer program is essentially an algorithm to tell the computer the exact steps to perform a specified task. Generally, when the algorithm is processing information, it will read the data from the input device or the storage address of the data, and write the result to the output device or a storage address for later call.

Algorithm is an independent method and idea to solve problems.

Five characteristics of the algorithm

1. Input: the algorithm has 0 or more inputs

2. Output: the algorithm has at least one or more outputs

3. Finiteness: the algorithm will automatically end after limited steps without infinite loop, and each step can be completed in an acceptable time

4. Certainty: every step in the algorithm has a definite meaning, and there will be no ambiguity

5. Feasibility: each step of the algorithm is feasible, that is, each step can be completed a limited number of times

Second attempt:

import time

start_time = time.time()

# Note that it is a double cycle
for a in range(0, 1001):
    for b in range(0, 1001-a):
        c = 1000 - a - b
        if a**2 + b**2 == c**2:
            print("a, b, c: %d, %d, %d" % (a, b, c))

end_time = time.time()
print("elapsed: %f" % (end_time - start_time))
print("complete!")

Operation results:

a, b, c: 0, 500, 500
a, b, c: 200, 375, 425
a, b, c: 375, 200, 425
a, b, c: 500, 0, 500
elapsed: 1.204760
complete!

Algorithm efficiency measurement

The execution time of the algorithm program can reflect the efficiency of the algorithm, that is, the advantages and disadvantages of the algorithm.

Simply relying on the running time to compare the advantages and disadvantages of the algorithm is not necessarily objective and accurate!

We assume that the time for the computer to perform each basic operation of the algorithm is a fixed time unit, so how many basic operations represent how many time units it will take. However, for different machine environments, the exact unit time is different, but the number of basic operations (i.e. how many time units it takes) of the algorithm is the same in the order of magnitude. Therefore, the influence of the machine environment can be ignored and the time efficiency of the algorithm can be reflected objectively.

The time efficiency of the algorithm can be expressed by "Big O notation".

"Large o notation": for monotonic integer function f, if there is an integer function g and real constant C > 0, so that for sufficiently large N, there is always f (n) < = C * g (n), that is, function g is an asymptotic function of F (ignoring the constant), which is recorded as f(n)=O(g(n)). In other words, in the sense of the limit towards infinity, the growth rate of function f is constrained by function g, that is, the characteristics of function f and function g are similar.

Time complexity: assuming that there is A function g such that the time taken by algorithm A to process the problem example with scale n is T(n)=O(g(n)), then O(g(n)) is called the asymptotic time complexity of algorithm A, referred to as time complexity for short, and recorded as T(n).

Worst time complexity

There are several possible considerations when analyzing the algorithm:

• How many basic operations does the algorithm need to complete the work, that is, the optimal time complexity

• How many basic operations does the algorithm need to complete the work, that is, the worst time complexity

• The average number of basic operations required for the algorithm to complete the work, that is, the average time complexity

We mainly focus on the worst case of the algorithm, that is, the worst time complexity.

Several basic calculation rules of time complexity

1. Basic operation, that is, there is only constant term, and its time complexity is considered to be O(1)

2. Sequential structure, and the time complexity is calculated by addition

3. Loop structure, and the time complexity is calculated by multiplication

4. Branch structure, with the maximum time complexity

5. When judging the efficiency of an algorithm, we often only need to pay attention to the highest order term of the number of operations, and other secondary terms and constant terms can be ignored

6. Without special instructions, the time complexity of the algorithm we analyze refers to the worst time complexity

Time complexity of first attempt:

T(n) = O(n*n\*n) = O(n^3)

Time complexity of the second attempt:

·T(n) = O(n*n*(1+1)) = O(n*n) = O(n^2)

It can be seen that the second algorithm we try has better time complexity than the first algorithm.

Common time complexity

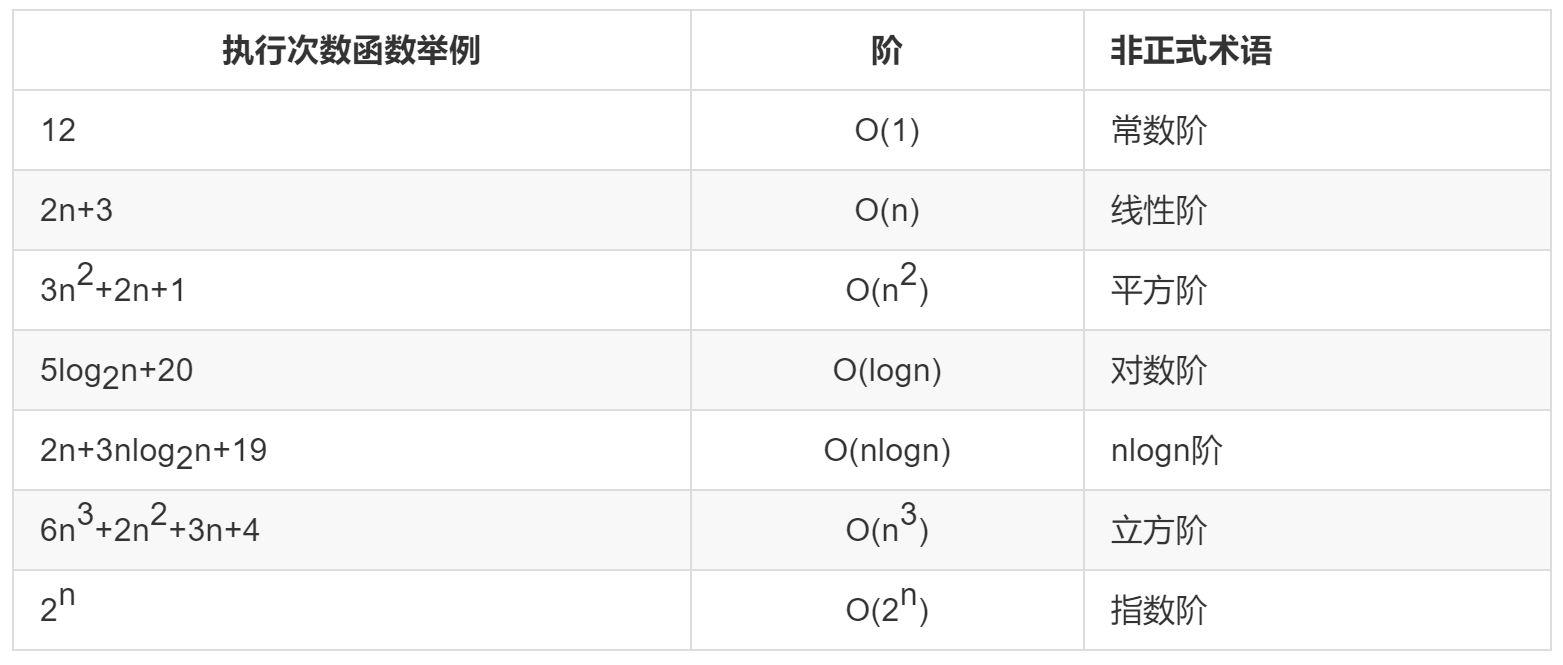
Note that log2n (base 2 logarithm) is often abbreviated to logn

Relationship between common time complexity

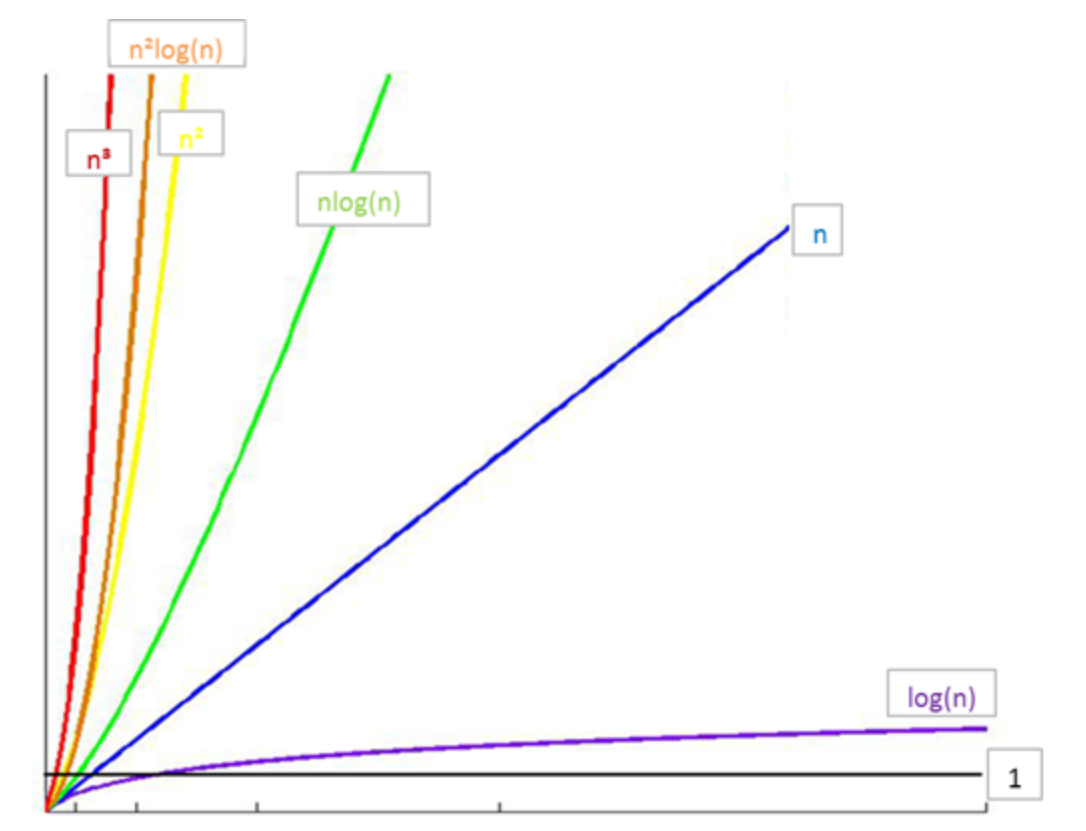
Time consumed from small to large:

O(1) < O(logn) < O(n) < O(nlogn) < O(n^2) < O(n^2logn) < O(n^3) < O(2^n) < O(n!) < O(n^n)

Python built-in type performance analysis

timeit module

The timeit module can be used to test the execution speed of a small piece of Python code.

class timeit.Timer(stmt='pass', setup='pass', timer=<timer function>)

Timer is a class that measures the execution speed of small pieces of code.

stmt parameter is the code statement to be tested;

The setup parameter is the setting required to run the code;

The timer parameter is a timer function, which is platform related.

timeit.Timer.timeit(number=1000000)

The object method in the Timer class that tests the execution speed of statements. The number parameter is the number of tests when testing the code. The default is 1000000. Method returns the average time spent executing code, in seconds of a float type.

list operation test

Test the time efficiency of different operations of list types:

def test1():
   l = []
   for i in range(1000):
      l = l + [i]
def test2():
   l = []
   for i in range(1000):
      l.append(i)
def test3():
   l = [i for i in range(1000)]
def test4():
   l = list(range(1000))
def test5():
    l = []
    for i in range(1000):
        l.extend([i])
def test6():
    l = []
    for i in range(1000):
        l.insert(0,i)
def test7():
   l = []
   for i in range(1000):
      l += [i]

from timeit import Timer

t1 = Timer("test1()", "from __main__ import test1")
print("+:",t1.timeit(number=1000), "seconds")
t2 = Timer("test2()", "from __main__ import test2")
print("append:",t2.timeit(number=1000), "seconds")
t3 = Timer("test3()", "from __main__ import test3")
print("[i for i in range]:",t3.timeit(number=1000), "seconds")
t4 = Timer("test4()", "from __main__ import test4")
print("list(range()):",t4.timeit(number=1000), "seconds")
t5 = Timer("test5()", "from __main__ import test5")
print("extend:",t5.timeit(number=1000), "seconds")
t6 = Timer("test6()", "from __main__ import test6")
print("insert(0):",t6.timeit(number=1000), "seconds")
t7 = Timer("test7()", "from __main__ import test7")
print("+=:",t7.timeit(number=1000), "seconds")

Execution results:

+: 2.5817442 seconds
append: 0.12733859999999986 seconds
[i for i in range]: 0.0662126999999999 seconds
list(range()): 0.022346999999999895 seconds
extend: 0.23506410000000022 seconds
insert(0): 0.7607794999999999 seconds
+=: 0.19090319999999972 seconds

pop operation test

x = range(2000000)
pop_zero = Timer("x.pop(0)","from __main__ import x")
print("pop_zero ",pop_zero.timeit(number=1000), "seconds")
x = range(2000000)
pop_end = Timer("x.pop()","from __main__ import x")
print("pop_end ",pop_end.timeit(number=1000), "seconds")

Operation results:

('pop_zero ', 1.9101738929748535, 'seconds')
('pop_end ', 0.00023603439331054688, 'seconds')

It can be seen from the results that the efficiency of the last element of pop is much higher than that of the first element of pop

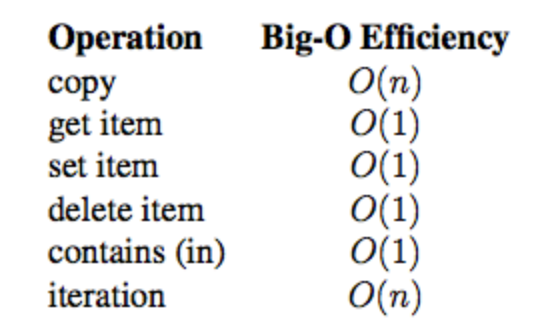
Time complexity of list built-in operations

Time complexity of built-in operation of dict

data structure

Data is an abstract concept. After classifying it, we can get the basic types in programming language. Such as int, float, char, etc. Data elements are not independent, and there are specific relationships. These relationships are structures. Data structure refers to the relationship between data elements in a data object.

Python provides us with many ready-made data structure types. The data structures defined by these systems and not defined by us are called Python's built-in data structures, such as lists, tuples and dictionaries. Some data organization methods are not directly defined in the python system. We need to define the organization methods to realize these data. These data organization methods are called Python extended data structures, such as stacks, queues, etc.

Difference between algorithm and data structure

The data structure only statically describes the relationship between data elements.

Efficient programs need to design and select algorithms based on data structures.

Program = data structure + algorithm

Conclusion: the algorithm is designed to solve practical problems, and the data structure is the problem carrier that the algorithm needs to deal with

Abstract data type

Abstract data type (ADT) refers to a mathematical model and a set of operations defined on the mathematical model. That is, data types and operations on data types are bound together for encapsulation. The purpose of introducing abstract data types is to separate the representation of data types and the implementation of operations on data types from the references of these data types and operations in programs, so as to make them independent of each other.

There are five most commonly used data operations:

• insert
• delete
• modify
• lookup
• sort