Sorting algorithm

Sorting algorithm (English: Sorting algorithm) is an algorithm that can arrange a string of data in a specific order.

Stability of sorting algorithm

Stability: the stable sorting algorithm will maintain the relative order of records with equal key values. That is, if -- sorting algorithm is stable, when there are two records R and S with equal key values, and R appears before S in the original list, R will also be before S in the sorted list. When equal elements are indistinguishable, such as integers, stability is not a problem. However, suppose that the following pairs of numbers will be sorted by their first number.

Bubble sorting

Bubble sort is a simple sort algorithm. It repeatedly traverses the sequence to be sorted, - compares two elements, and swaps them if they are in the wrong order. The work of traversing the sequence is repeated until there is no need to exchange, that is, the sequence has been sorted. The name of this algorithm comes from the fact that smaller elements will slowly "float" to the top of the sequence through exchange.

Illustration

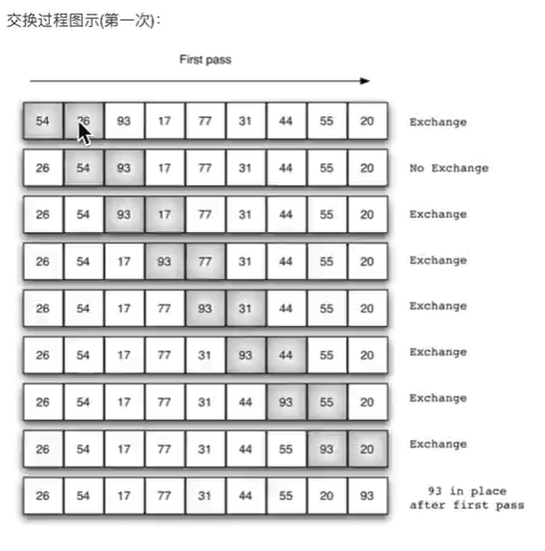
realization

# coding: utf-8


def bubble_sort(alist):
    """Bubble sorting"""
    n = len(alist)
    for j in range(n-1):            # for j in rang(len(alist)-1,0,-1):
        count = 0
        for i in range(0, n-1-j):       # for i in range(j):
            # From beginning to end
            if alist[i] > alist[i+1]:
                alist[i], alist[i+1] = alist[i+1], alist[i]
                count += 1
        if 0 == count:
            return


if __name__ == "__main__":
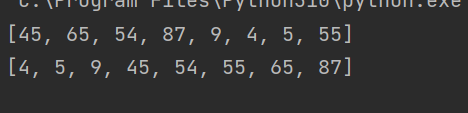
    li = [45, 65, 54, 87, 9, 4, 5, 55]
    print(li)
    bubble_sort(li)
    print(li)

Operation results

Time complexity

Optimal time complexity: O(n) (indicates traversal -- no elements can be exchanged for each discovery)
(end of sorting.)
Worst time complexity: o(n^2)
Stability: stable

Select sort

Selection sort is a simple and intuitive sorting algorithm. Its working principle is as follows.

First, find the smallest (large) element in the unordered sequence and store it at the beginning of the sorted sequence. Then, continue to find the smallest (large) element from the remaining unordered elements, and then put it at the end of the sorted sequence. And so on until all elements are sorted. The main advantage of selective sorting is related to data movement. If a dollar; If the element is in the correct final position, it will not be moved. Select sort to exchange a pair of elements each time, and at least - of them will be moved to their final position. Therefore, sort the table of n elements and exchange at most n-1 times in total. Among all the sorting methods that completely rely on exchange to move elements, selective sorting is a very good one.

Illustration

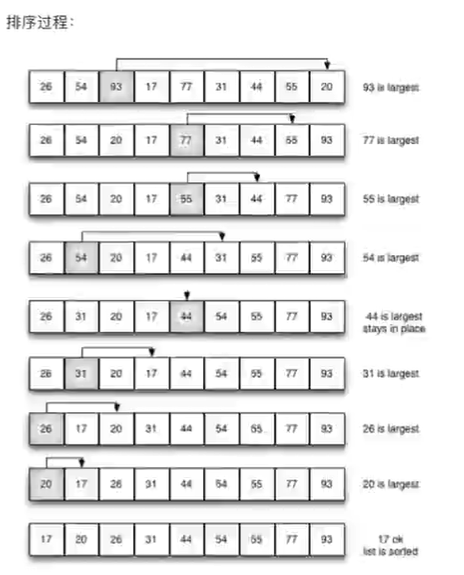
realization

def select_sort(alist):
    """Select sort"""
    n = len(alist)
    for j in range(n-1):    # j: 0~ n-2
        min_index = j
        for i in range(j+1, n):
            if alist[min_index] > alist[i]:
                min_index = i
        alist[j], alist[min_index] = alist[min_index], alist[j]


if __name__ == "__main__":
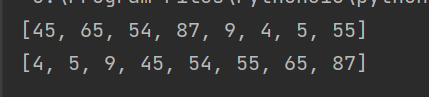
    li = [45, 65, 54, 87, 9, 4, 5, 55]
    print(li)
    select_sort(li)
    print(li)

Operation results

Time complexity

Optimal time complexity: O(n^2)
Worst time complexity: O(n^2)
Stability: unstable (considering the maximum selection of ascending order each time)

Insert sort

Insertion sort (English: Insertion Sort) is a simple and intuitive sorting algorithm. Its working principle is to build an ordered sequence, scan the unordered data from back to front in the sorted sequence, find the corresponding position and insert it. In the implementation of insertion sorting, in the process of scanning from back to front, it is necessary to repeatedly move the sorted elements backward step by step to provide insertion space for the latest elements.

Illustration

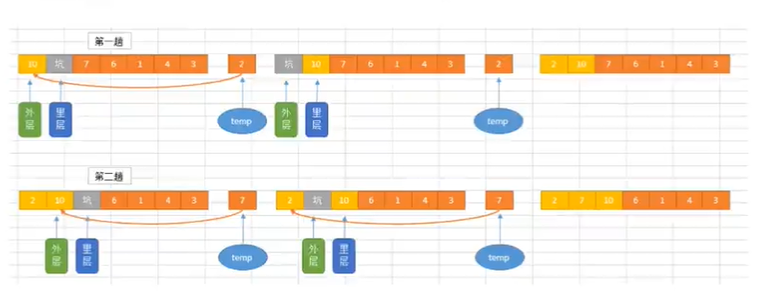
realization

# coding : utf-8

def insert_sort(alist):
    """Insert sort"""
    n = len(alist)
    for j in range(1, n):       # How many elements are taken from the unordered sequence on the right to perform such a process
        i = j       # i represents the starting value of inner loop
        while i > 0:    # Execute to take the first element from the unordered sequence on the right, that is, the element at i position, and then insert it into the previous position
            if alist[i] < alist[i-1]:
                alist[i], alist[i-1] = alist[i-1], alist[i]
                i -= 1
            else:
                break


if __name__ == "__main__":
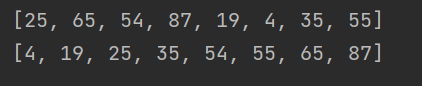
    li = [25, 65, 54, 87, 19, 4, 35, 55]
    print(li)
    insert_sort(li)
    print(li)

Operation results

Time complexity

Optimal time complexity: O(n) (in ascending order, the sequence is already in ascending order
Status)
Worst time complexity: 0(n^2)
Stability: stable