1, What is a binary sort tree?
The binary sorting tree is either an empty binary tree or a binary tree with the following characteristics:
- In a binary sort tree, if its root node has a left subtree, the values of all nodes in the left subtree are smaller than those of the root node;
- In a binary sort tree, if its root node has a right subtree, the values of all nodes in the right subtree are greater than those of the root node;
- The left and right subtrees of binary sort trees are also required to be binary sort trees.
As shown in the figure below: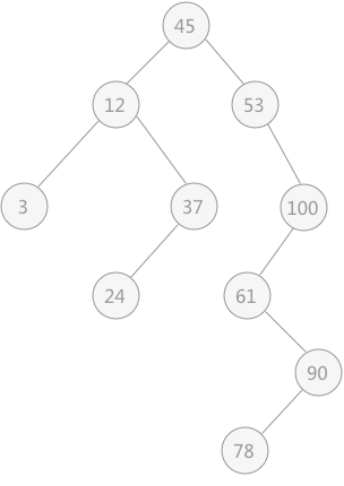

2, Python implementation of binary sort tree
Insertion of binary sort tree
Insert: start from the root node and compare with the keyword one by one. If the value is smaller than the root node to the left and larger than the root node to the right, it points to the keyword when the subtree is empty.
class Node(object): """Encapsulation of binary tree nodes""" def __init__(self, element=None, lchild=None, rchild=None): self.element = element self.lchild = lchild self.rchild = rchild def __str__(self): return '<node:%d>' % (self.element) class BinarySortTree(object): """Encapsulation of binary sort tree""" def __init__(self): self.root = None def is_empty(self): return self.root == None def __add__(self, item): """ //Insert elements in the tree: 1. If it is an empty binary tree, point the root node to the node where the element is inserted 2. If it is not empty, compare the size with the root node to find the right subtree if it is larger than the root node and the left subtree if it is smaller than the root node :param item: :return: """ node = Node(item) if self.is_empty(): self.root = node bt = self.root while True: rootItem = bt.element # If the node element is larger than the insert element, look for the left subtree if rootItem > item: if bt.lchild == None: bt.lchild = node bt = bt.lchild # If the element of the node is smaller than the insert element, look for the right subtree elif rootItem < item: if bt.rchild == None: bt.rchild = node bt = bt.rchild else: return def breadth_travel(self): """Using queue to realize hierarchical traversal of tree""" if self.is_empty(): return queue = [] queue.append(self.root) while queue: cur = queue.pop(0) print(cur.element, end=',') if cur.lchild != None: queue.append(cur.lchild) if cur.rchild != None: queue.append(cur.rchild) print()
Search of binary sort tree
Find: compare the value and key words of a node, if they are equal, it indicates that the node is found, and output the node; if it is less than the value of the node, it searches to the left subtree of the node, if it is greater than the value of the node, it searches to the right subtree, recursively, and finally returns the Boolean value or the found node.
def searchDetail(self, root, parent, key): """ //Search whether the specified element is in the tree :param root: Root node :param parent: Parent node :param key: Elements for user search :return:return parent For the convenience of deletion """ if self.is_empty(): return False, root, parent while root: # If the found node element is equal to the user's search, the node object is returned directly if root.element == key: return True, root, parent # If the found node element is greater than the value of user search, continue to search to the left subtree of the node elif root.element > key: parent = root root = root.lchild # If the node element found is less than the value searched by the user, continue searching to the right subtree of the node else: parent = root root = root.rchild return False, root, None
The deletion of two pronged sorting tree
1. Delete node as leaf node
The deleted node has no left sub tree or right sub tree, that is, the deleted node is a leaf node. There are two situations:
1. The leaf node is the root node of the binary sort tree, that is, there is only one node in the binary sort tree, so you only need to set the root pointer to null
2. The leaf node has a parent node. Set the pointer of the parent node to the delete node to null.
2. The deleted node only has left subtree or right subtree
After deleting a node, point the parent node pointer to the subtree
3. There are left and right subtrees at the same time
If there are left and right subtrees at the same time, the binary sort tree can be traversed in the middle order, and the position of the deleted node can be replaced by the predecessor or successor node of the node to be deleted.
Method 1: make the left subtree of node p as the left subtree of its parents' node, and the right subtree of node p as the right subtree of its direct predecessor node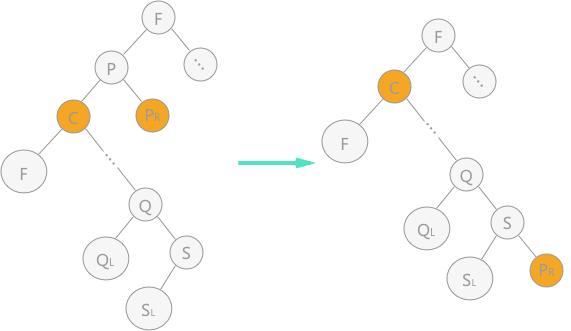
Similarly, if the deleted node is the right subtree node of the root node, the right subtree of node p is the right subtree of its parent node, and the left subtree of node p is the left subtree of its own successor node.
def __delete__(self, key): """ //Delete the node elements of the binary sort tree: 1. If the leaf node is deleted, delete it directly 2. If there is only a left or right subtree, after deleting the node, link the subtree to the parent node 3. There are both left subtree and right subtree, which can be solved by two methods :param key: :return: """ # Find the node corresponding to the deleted element, get whether it exists, get the node and its parent node isExist, node, parentNode = self.searchDetail(self.root, None, key) # If the node does not exist if not isExist: print('Elements to delete%d non-existent' %(node.element)) return # If there is no root if not self.root: print('thr tree is null') return # If you are dealing with the root node, do not deal with it if node == self.root: print('Cannot delete root node') return # 1. If a leaf node is deleted, delete it according to its parent node if not node.lchild and not node.rchild: # Judge whether it is the right child or the left child of the parent node if parentNode.rchild == node: parentNode.rchild = None if parentNode.lchild == node: parentNode.rchild = None # 2. If only the right or left subtree exists, link the child node of the node to the parent node and delete the node # If it's a right subtree if not node.lchild and node.rchild: parentNode.rchild = node.rchild # If it's a left subtree if not node.rchild and node.lchild: parentNode.lchild = node.lchild # 3. Both left and right subtrees exist if node.lchild and node.rchild: # Classified discussion, delete the left or right child of the parent node # If the direct parent node of the node is found, make the left subtree of the node node the left subtree of its parent node, # Point the rightmost node of the right subtree of the left subtree of the node to the right subtree of the node if parentNode.lchild == node: parentNode.lchild = node.lchild prevNode = node.lchild while prevNode.rchild: prevNode = prevNode.rchild # prevNode refers to the direct precursor of node (node in front of node when traversing in medium order) prevNode.rchild = node.rchild # If you delete the right child of the parent node, point the right child of the parent node to the right child of the node # Point the leftmost node of the left subtree of the right child of the node to the left subtree of the node elif parentNode.rchild == node: parentNode.rchild = node.rchild prevNode = node.rchild # prevNode refers to the direct successor of a node (in the middle order traversal, the node following the node) while prevNode.lchild: prevNode = prevNode.lchild prevNode.lchild = node.lchild
Method 2: replace node p with its direct predecessor (or direct successor), and delete its direct predecessor (or direct successor) in the binary sort tree. In the middle order traversal of the left graph, the direct precursor of node p is node s, so node s is directly used to cover node p
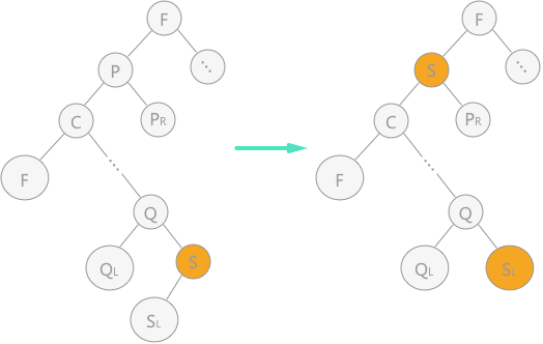
The code of method 2 is similar to method 1, so it will not be written here.
General idea:
First, find the rightmost node of the right subtree of the left subtree of the node (that is, find the node smaller than the deleted node but closest to the size of the deleted node), let the right child of the parent node of the rightmost node point to the left child of the rightmost node, let the left child of the parent node point to the rightmost node of the right subtree of the left subtree of the node, and the left child of the rightmost node point to the node The right child points to the right child of the node.
Test code:
if __name__ == '__main__': binarySortedTree = BinarySortTree() nums = [6, 4, 2, 3, 5, 8, 7, 9] for num in nums: binarySortedTree.__add__(num) # binarySortedTree.__add__(4) # binarySortedTree.__add__(6) binarySortedTree.breadth_travel() root = binarySortedTree.root print('Detailed search....') isExist, node, parentNode = binarySortedTree.searchDetail(root, None, 7) print('Search results:',isExist) print("Nodes found:" ,node) print('Search node's parent:', parentNode) # binarySortedTree.__delete__(2) # binarySortedTree.breadth_travel() binarySortedTree.__delete__(8) binarySortedTree.breadth_travel() 6,4,8,2,5,7,9,3, //Detailed search.... //Search results: True //Nodes found: <node:7> //Search node's parent: <node:8> 6,4,9,2,5,7,3,