1. Find the sum of 1 + (1 + 2) + (1 + 2 + 3) +... + (1 + 2 + 3 +... + n)

Find the sum of 1 + (1 + 2) + (1 + 2 + 3) +... + (1 + 2 + 3 +... + n)

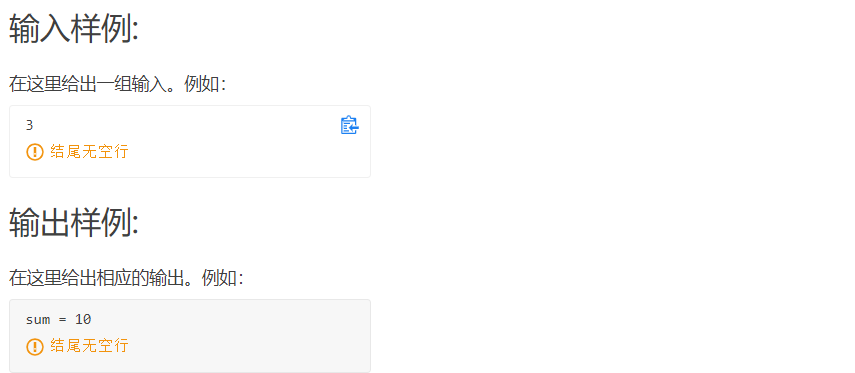
Input format:

Enter an integer.

Output format:

Output the desired sum.

The code is as follows:

n=int(input())
sum=0
for i in range(1,n+1):
   for j in range(1,i+1):
    sum=sum+j
print("sum = %d" %sum)
 

 2. Maximum common factor and minimum common multiple

Find the maximum common factor and minimum common multiple of two positive integers ， A and B ， respectively.

The greatest common factor of two numbers refers to the largest of the common divisors of a,b.

The least common multiple of two numbers refers to the smallest multiple shared by a and B.

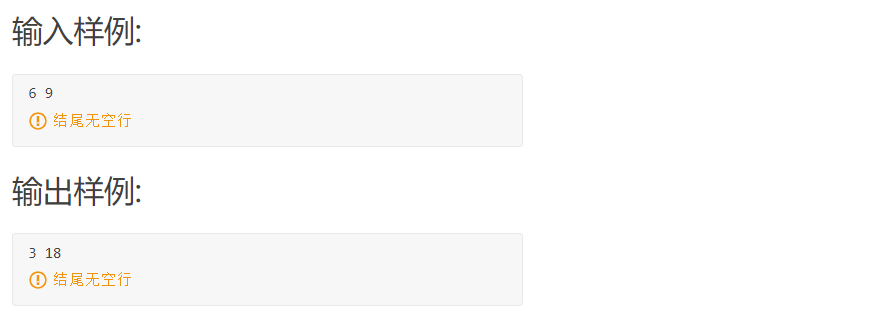
Input format:

Give two numbers a,b in one line (1 < = a,b < = 1000000000)

Output format:

Separate the maximum common factor and minimum common multiple of ， A and B ， in a row with spaces.

 The code is as follows:

def gcd(a, b):
    if a % b == 0:
        return b
    else:
        return gcd(b, a % b)
n, m = input().split()
n = int(n)
m = int(m)
print('{:d} {:d}'.format(gcd(n, m), n*m//gcd(n, m)))

 

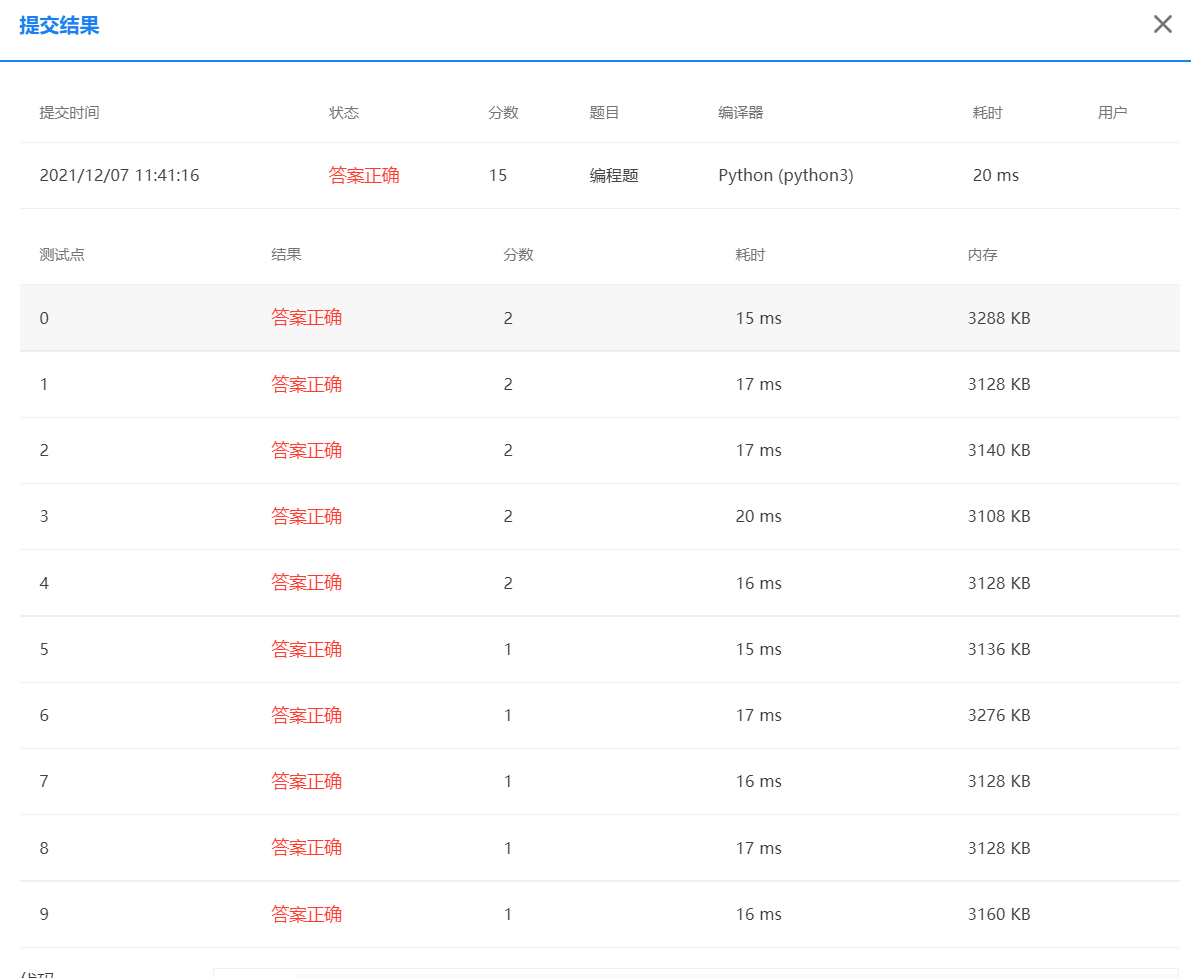
3. Number of daffodils

Narcissus number refers to an n-bit positive integer (n ≥ 3), and the sum of the N powers of the numbers in each bit is equal to itself. For example, 153 = 1 × one × 1+5 × five × 5+3 × three × 3.

This problem requires writing a program to calculate the number of all N-bit daffodils.

Input format:

Input gives a positive integer N (3 ≤ N ≤ 5) in one line

Output format:

Output the number of all N-bit daffodils in ascending order, and each number occupies one line.

The code is as follows:

n=int(input())
for i in range(10**(n-1),10**(n)):
    sum=0
    for p in str(i):
        sum+=(int(p))**n
    if sum==i:
        print(i)
    

 

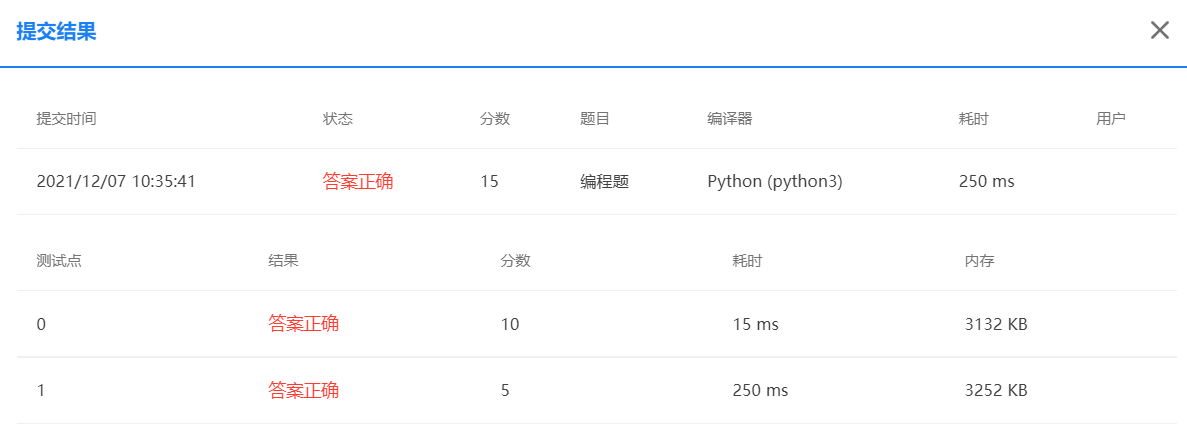
4. Exhaustive problem - moving bricks

A construction site needs to carry bricks. It is known that a man carries three bricks, a woman carries two bricks and a child carries one brick. If you want to use n people to move n bricks, how many moving methods are there?

Input format:

The input gives a positive integer n in one line.

Output format:

The output shows a scheme in each line, and outputs the number of men CNT according to the format of "men = cnt_m, women = cnt_w, child = cnt_c"_ m. Number of women CNT_ w. Number of children CNT_ c. Notice that there is a space on each side of the equal sign and a space after the comma.

If no matching scheme is found, "None" is output

 

The code is as follows:

n=int(input())
count=0
for cnt_m in range (n):
    for cnt_w in range (n):
        for cnt_c in range (n):
            if ((cnt_m + cnt_w + cnt_c == n) and (cnt_m * 3 + cnt_w * 2 + cnt_c*0.5 == n)):
                count+=1
                print(f'men = {cnt_m}, women = {cnt_w}, child = {cnt_c}')
if(count==0):
    print('None')

 

5. Display prime numbers within the specified range

Input the integer m, store all prime numbers greater than 1 and less than the integer m into the specified array (the array can only store 100 prime numbers at most, and if it exceeds, it will prompt "OVERFLOW"), output each prime number - if the input m ≤ 2, it will prompt "NO", and the program will terminate. Note: prime number, also known as prime number, refers to a natural number greater than 1 that cannot be divided by other natural numbers except 1 and the integer itself.

Input format:

Enter a non-zero integer.

Output format:

The output format of prime numbers is 5 columns wide, right aligned and 15 per row.

The code is as follows:

m=int(input())
if m<=2:
    print("NO")
else:
    list=[]
    for i in range(2,m):
        if i >1:
            for j in range(2,i):
                if i%j==0:
                    break
            else:
                list.append(i)
    if len(list)>100:
        print("OVERFLOW")
    else:
        o=0
        for p in list:
            q=str(p)
            print("%5d"%p,end="")
            o=o+1
            if o%15==0:
                print("\n",end="")

 

 

6. Taylor expansion for sinx approximation

The polynomial for finding sinx approximation by Taylor expansion is:

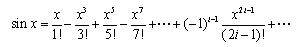
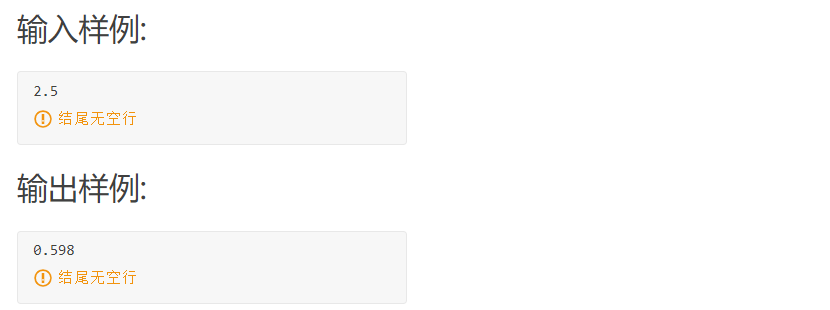
Enter x to find the approximate value of sinx, and the error shall not be greater than 0.00001.

Input format:

Enter a real data directly. There are no additional characters.

Output format:

Directly output the real result with 3 decimal places.

 

The code is as follows:

import math
x=float(input())
a=x
b=1
f=1
n=f*(a/b)
i=1
sum=n
while math.fabs(n)>1e-5:
    i=i+2
    a=x**i
    b=b*(i-1)*i
    f=f*(-1)
    n=f*a/b
    sum=sum+n
print("%.3f"%sum)