The purpose of regression is to predict the numerical target value. A sentence input to write a target value calculation formula is the so-called regression equation, and the process of calculating the regression coefficient is regression. Once you have these regression coefficients, it's very easy to make predictions at a given input. The specific method is to multiply the regression coefficient by the input value, and then add all the results together to get the predicted value.
How to get the regression equation from a lot of data? Jiading input data is stored in matrix X and regression coefficient is stored in vector w, then for a given data x1, the prediction result will pass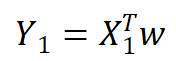
give. Now there are some x and corresponding y. how can we find w? A common method is to find the W with the smallest error. The error here refers to the difference between the predicted y value and the real y value. The simple accumulation of the error will make the positive difference and negative difference offset each other, so the square error is adopted:
def loadDataSet(filename):
numFeat = len(open(filename).readline().split('\t'))-1
dataMat=[]
labelMat=[]
fr = open(filename)
for line in fr.readlines():
lineArr = []
curLine = line.strip().split('\t')
for i in range(numFeat):
lineArr.append(float(curLine[i]))
dataMat.append(lineArr)
labelMat.append(float(curLine[-1]))
return dataMat,labelMat
#The last value in each line of the default file is the target value
def standRegres(xArr,yArr):
xMat = mat(xArr)
yMat = mat(yArr).T
#First read x,y and save them in the matrix
xTx =xMat.T*xMat
if linalg.det(xTx) == 0.0:
print("This matrix is singular,cannot do inverse")
return
#If the determinant of the matrix is 0, an error will occur when calculating the inverse matrix
#linalg,det() can be called directly to evaluate determinants
ws = xTx.I*(xMat.T*yMat)
return ws
#Determinant non-zero return w
"""
This function is used to calculate the best fit line
"""
xArr,yArr = loadDataSet('F:\python\machinelearninginaction\Ch08\ex0.txt')
print(xArr[0:2])
ws = standRegres(xArr, yArr)
print(ws)[[1.0, 0.067732], [1.0, 0.42781]]
[[3.00774324]
[1.69532264]]
The first value is always equal to 0, that is, X0, and we assume that the offset is a constant. The second value X1 is the abscissa value
ws stores the regression coefficients. When using the inner product to predict y, the first bit will be multiplied by the previous constant X0, and the second will be multiplied by the input variable x1. Because X0=1 is assumed, y=ws[0]+ws[1]*X1 will be finally obtained. Y here is actually a prediction tree. In order to distinguish it from the true y value, it is recorded as yhhat. Next, calculate yhhat with the value of the new ws
xMat = mat(xArr) yMat = mat(yArr) import matplotlib.pyplot as plt fig = plt.figure() ax = fig.add_subplot(111) ax.scatter(xMat[:,1].flatten().A[0],yMat.T[:,0].flatten().A[0]) xCopy = xMat.copy() xCopy.sort(0) yHat = xCopy*ws ax.plot(xCopy[:,1],yHat) plt.show()
By calculating the matching degree between the predicted value yhhat sequence and the real value y sequence -- calculating the correlation coefficient of the two sequences, we can compare the results. It can be calculated by corrcoef(yEstimate,yActual)
yHat = xMat*ws print(corrcoef(yHat.T,yMat))
[[1. 0.98647356]
[0.98647356 1. ]]
The matrix contains the correlation coefficients of all pairwise combinations. The data on the diagonal is 1.0. Because yhhat matches itself perfectly
Locally weighted linear regression (LWLR)
When dealing with linear regression, we must try our best to avoid the phenomenon of under fitting, and some deviations can be introduced into the estimation, so as to reduce the mean square error of prediction. One method is locally weighted linear regression. We give a certain weight to each point near the point to be predicted, and then carry out ordinary regression based on the minimum mean square error. Like kNN, this algorithm needs to select and remove the data subset used for each prediction play. The form of regression coefficient w solved by this algorithm is as follows:
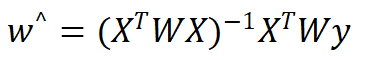
Where w is a matrix used to give weight to each data point.
LWLR uses "kernel" to give higher weight to nearby points, and the most commonly used is Gaussian kernel.
In this way, a weight matrix w with only diagonal elements is constructed, and the closer the point x is to X (i), the greater the w(i,i). The above formula contains a parameter k that needs to be specified by the user, which determines how much weight is given to nearby points, and it is also the only parameter to be considered.
def lwlr(testPoint,xArr,yArr,k=1.0):
xMat = mat(xArr)
yMat = mat(yArr).T
m = shape(xMat)[0]
weights = mat(eye((m)))
# Read the data and create the matrix, and then create the diagonal weight matrix weights
for j in range(m):
diffMat = testPoint - xMat[j,:]
weights[j,j] = exp(diffMat*diffMat.T/(-2.0*k**2))
xTx = xMat.T*(weights*xMat)
#The algorithm traverses the data set and calculates the corresponding weight value of each sample point
#As the distance between the sample point and the point to be predicted increases, the weight handout decays exponentially
#The acceleration parameter k controls the rate of attenuation
if linalg.det(xTx) == 0.0:
print("This matrix is singular,cannot do inverse")
return
ws = xTx.I*(xMat.T*(weights*yMat))
return testPoint*ws
def lwlrTest(testArr,xArr,yArr,k=1.0):
m = shape(testArr)[0]
yHat = zeros(m)
for i in range(m):
yHat[i] = lwlr(testArr[i],xArr,yArr,k)
return yHat
#Calling lwlr() for each point in the dataset helps solve the size of k
"""
The purpose of this code is:
given x At any point in the space, the corresponding predicted value is calculated yHat.
"""
k=0.003
k=0.01
It can be seen that a very good effect is obtained when k=0.01, while k=0.003 includes too many noise points, and the fitted straight line is too close to the data points, so it is an example of over fitting. Next, quantitative analysis of over fitting and under fitting will be carried out.
Barber, run, get express, refuse three minutes of heat