27. Remove element
Give you an array num and a value val, you need In situ Removes all elements with a value equal to val and returns the new length of the array after removal.
Do not use extra array space, you must only use O(1) extra space and In situ Modify the input array.
The order of elements can be changed. You don't need to consider the elements in the array that exceed the new length.
Example 1:
given nums = [3,2,2,3], val = 3, The function should return a new length of 2, also nums The first two elements in are both 2. You don't need to consider the elements in the array that exceed the new length.
Example 2:
given nums = [0,1,2,2,3,0,4,2], val = 2, The function should return a new length of 5, also nums The first five elements in are 0, 1, 3, 0, 4. Note that these five elements can be in any order. You don't need to consider the elements in the array that exceed the new length.
explain:
Why is the returned value an integer, but the output answer is an array?
Note that the input array is passed by * * reference * *, which means that modifying the input array in the function is visible to the caller.
You can imagine the internal operation as follows:
// nums is passed by reference. That is, no copy of the arguments is made
int len = removeElement(nums, val);
// Modifying the input array in the function is visible to the caller.
// According to the length returned by your function, it will print all elements within that length range in the array.
for (int i = 0; i < len; i++) {
print(nums[i]);
}
class Solution {
public int removeElement(int[] nums, int val) {
int length = nums.length;
for(int i = 0;i<length;i++){
if(nums[i]==val){
nums[i]=nums[length-1];
i--;
length--;
}
}
return length;
}
}
class Solution {
public:
int removeElement(vector<int>& nums, int val) {
int length = nums.size();
for(int i = 0;i<length;i++){
if(nums[i] == val){
nums[i] = nums[length-1];
length--;
i--;
}
}
return length;
}
};
26. Remove duplicates from the sort array
Given a sort array, you need to** In situ **Delete the repeated elements so that each element appears only once, and return the new length of the array after removal.
Do not use additional array space, you must In situ Modify the input array and do it with O(1) extra space.
Example 1:
Given array nums = [1,1,2], The function should return a new length of 2, And the original array nums The first two elements of are modified to 1, 2. You don't need to consider the elements in the array that exceed the new length.
Example 2:
given nums = [0,0,1,1,1,2,2,3,3,4], The function should return a new length of 5, And the original array nums The first five elements of are modified to 0, 1, 2, 3, 4. You don't need to consider the elements in the array that exceed the new length.
class Solution {
public int removeDuplicates(int[] nums) {
int i = 0,j= 1;
while(i<nums.length&&j<nums.length){
if(nums[i]!=nums[j]){
i++;
nums[i] = nums[j];
}
j++;
}
return i+1;
}
}
class Solution {
public:
int removeDuplicates(vector<int>& nums) {
if(nums.empty()) return 0;
int i=0,j=1,size = nums.size();
while( i<size&& j<size){
if(nums[i] != nums[j]){
i++;
nums[i] = nums[j];
}
j++;
}
return i+1;
}
};
80. Delete duplicates in the sort array II
Medium difficulty 252
Given a sort array, you need to** In situ **Delete the repeated elements so that each element can appear twice at most, and return the new length of the array after removal.
Do not use additional array space, you must** In situ Modify the input array * * and complete it with O(1) additional space.
Example 1:
given nums = [1,1,1,2,2,3], Function should return a new length length = 5, And the first five elements of the original array are modified to 1, 1, 2, 2, 3 . You don't need to consider the elements in the array that exceed the new length.
Example 2:
given nums = [0,0,1,1,1,1,2,3,3], Function should return a new length length = 7, And the first five elements of the original array are modified to 0, 0, 1, 1, 2, 3, 3 . You don't need to consider the elements in the array that exceed the new length.
public int removeDuplicates(int[] nums) {
int i =0,j= 1;
int n= 1;
while(i<nums.length&&j<nums.length){
if(nums[i]!=nums[j]||n!=2){
n = nums[i] == nums[j] ? 2:1;
i++;
nums[i] = nums[j];
}
j++;
}
return i+1;
}
189. Rotate array
Easy 629
Given an array, move the elements in the array K positions to the right, where k is a non negative number.
Example 1:
input: [1,2,3,4,5,6,7] and k = 3 output: [5,6,7,1,2,3,4] explain: Rotate 1 step to the right: [7,1,2,3,4,5,6] Rotate 2 steps to the right: [6,7,1,2,3,4,5] Rotate 3 steps to the right: [5,6,7,1,2,3,4]
Example 2:
input: [-1,-100,3,99] and k = 2 output: [3,99,-1,-100] explain: Rotate 1 step to the right: [99,-1,-100,3] Rotate 2 steps to the right: [3,99,-1,-100]
explain:
- Think of as many solutions as possible. There are at least three different ways to solve this problem.
- The in-situ algorithm with spatial complexity O(1) is required.
Method 1: extra array method:
public void rotate(int[] nums, int k) {
k=k%nums.length;
int[] m = new int[k];
System.arraycopy(nums,nums.length-k,m,0,k);
System.arraycopy(nums,0,nums,k,nums.length-k);
System.arraycopy(m,0,nums,0,k);
}
Method 2: violence cycle k times method
public void rotate1(int[] nums, int k) {
k=k%nums.length;
for(int j = 0;j<k;j++){
int lastOne = nums[nums.length-1];
for(int i = nums.length-1;i>0;i++){
nums[i] = nums[i-1];
}
nums[1] = lastOne;
}
}
Method 3: use inversion
This method is based on the fact that when we rotate the array K times, k%nk%n tail elements will be moved to the head, and the remaining elements will be moved back.
In this method, we first invert all elements. Then reverse the first k elements and then the next n-kn − k elements to get the desired result.
Suppose n=7n=7 and k=3k=3.
Original array : 1 2 3 4 5 6 7 After reversing all numbers : 7 6 5 4 3 2 1 Before inversion k After a number : 5 6 7 4 3 2 1 After reversal n-k After a number : 5 6 7 1 2 3 4 --> result
- Java
public class Solution {
public void rotate(int[] nums, int k) {
k %= nums.length;
reverse(nums, 0, nums.length - 1);
reverse(nums, 0, k - 1);
reverse(nums, k, nums.length - 1);
}
public void reverse(int[] nums, int start, int end) {
while (start < end) {
int temp = nums[start];
nums[start] = nums[end];
nums[end] = temp;
start++;
end--;
}
}
}
Complexity analysis
- Time complexity: O(n)O(n). nn elements were inverted a total of 3 times.
- Spatial complexity: O(1)O(1). No extra space was used.
41. Missing first positive number
Give you an unordered array of integers. Please find the smallest positive integer that does not appear in it.
Example 1:
input: [1,2,0] output: 3
Example 2:
input: [3,4,-1,1] output: 2
Example 3:
input: [7,8,9,11,12] output: 1
Tips:
The time complexity of your algorithm should be O(n) and can only use additional space at the constant level.
Treat arrays as hash tables
This idea was first seen in the book sword finger off. Interested friends may wish to ask this question: Sword finger Offer 03 Duplicate number in array . The following is a brief description:
- Because the topic requires us to "only use constant level space", the number to be found must be in the interval of [1, N + 1] left closed and right closed (where n is the length of the array). Therefore, we can use the original array as a hash table. In fact, the hash table itself is also an array;
- The number we are looking for is in [1, N + 1], and we don't need to find the last element n + 1. Because we only return n + 1 when the previous n elements cannot be found;
- Then, we can take this idea: put the number 1 in the position with subscript 0 and the number 2 in the position with subscript 1, and sort out the array according to this idea. Then we traverse the array again. The value of the first encountered is not equal to the number of subscripts, which is the first positive number we want to find.
- This idea is equivalent to writing our own hash function. The rule of this hash function is particularly simple, that is, the number with value I is mapped to the position with subscript i - 1.
Let's see how this algorithm is applied to example 2.
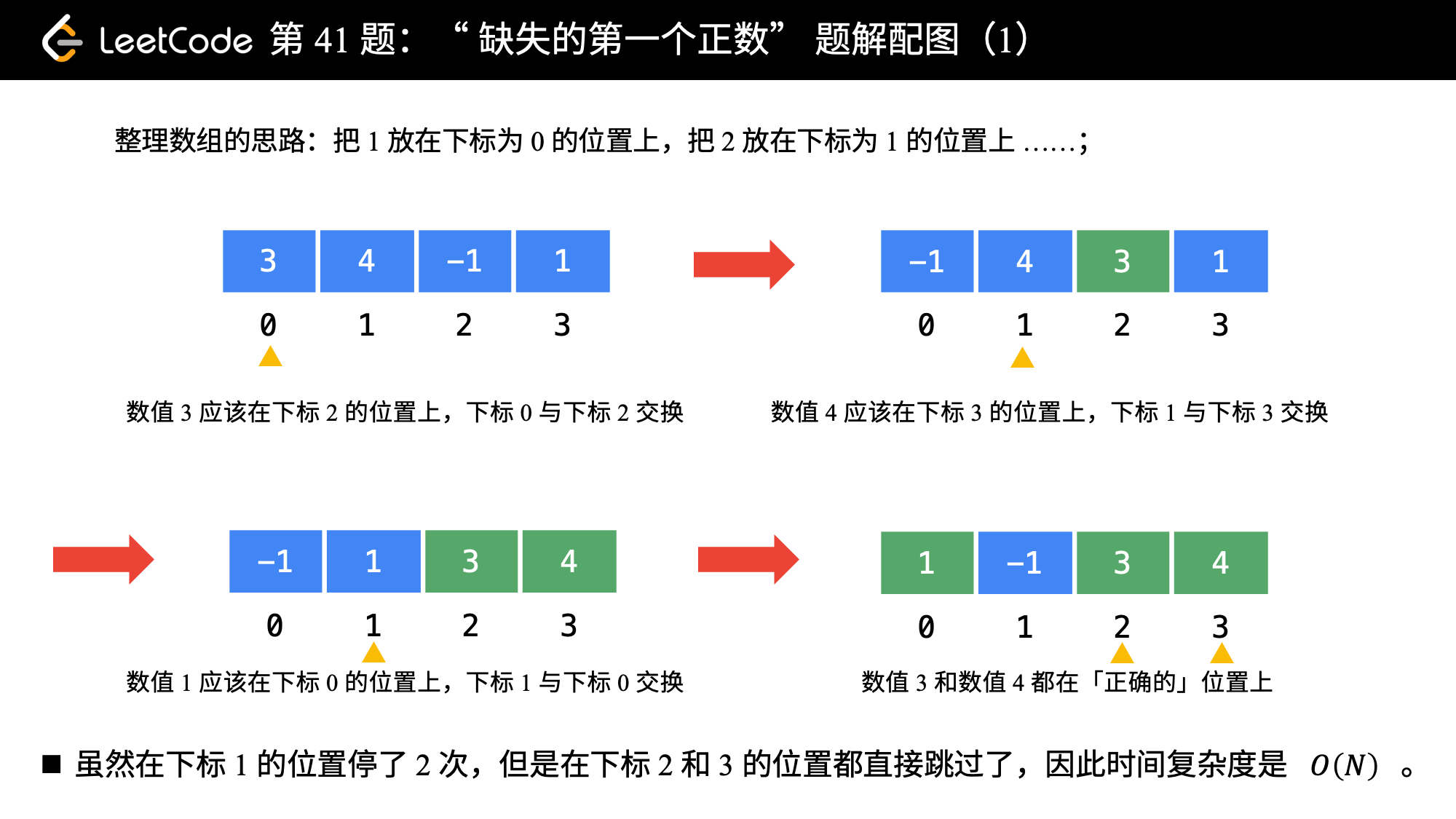
Note: understand the following code nums [nums [i] - 1]= The role of nums [i].
public class Solution {
public int firstMissingPositive(int[] nums) {
int len = nums.length;
for (int i = 0; i < len; i++) {
while (nums[i] > 0 && nums[i] <= len && nums[nums[i] - 1] != nums[i]) {
int temp = nums[nums[i] - 1];
nums[nums[i] - 1] = nums[i];
nums[i] = temp;
}
}
for (int i = 0; i < len; i++) {
if (nums[i] != i + 1) {
return i + 1;
}
}
return len + 1;
}
}
299. Number guessing game
Simple difficulty 82
Are you playing with your friends Bulls and Cows The rules of the game are as follows:
- You write a secret number and ask your friend to guess what the number is.
- Every time a friend guesses, you will give him a hint to tell him how many digits in the guessed number belong to the number and the exact position are guessed correctly (called "Bulls", bull), and how many digits belong to the number but the position is wrong (called "Cows", cow).
- The friend continues to guess according to the hint until he guesses the secret number.
Please write A function that returns A prompt according to the secret number and the guess number of friends. The format of the returned string is xAyB. x and y are numbers, A represents A bull and B represents A cow.
- xA indicates that there are x digits in the secret number, and the positions are consistent with the secret number.
- yB indicates that there are y digits in the secret number, but the position is inconsistent with the secret number.
Please note that secret numbers and friends' guesses may contain duplicate numbers. Each number can only be counted once.
Example 1:
input: secret = "1807", guess = "7810" output: "1A3B" explain: 1 Bulls and 3 cows. The bull is 8 and the cow is 0, 1 And 7.
Example 2:
input: secret = "1123", guess = "0111" output: "1A1B" explain: The first 1 in my friend's guess is a bull, and the second or third 1 can be regarded as a cow.
Note: you can assume that both secret numbers and friends' guesses contain only numbers, and their lengths are always equal.
public static String getHint(String secret, String guess) {
int A =0;
int[] snums =new int[10];
int[] gnums =new int[10];
for(int i = 0;i<secret.length();i++){
if(secret.charAt(i) == guess.charAt(i))
A++;
else{
snums[secret.charAt(i)-'0'] += 1;
gnums[guess.charAt(i)-'0'] += 1;
}
}
int B = 0;
for(int i = 0;i<10;i++){
B += Math.min(snums[i],gnums[i]);
}
return A+"A"+B+"B";
}
134. Gas stations
There are N gas stations on a ring road, of which the ith gas station has gasoline gas[i] liters.
You have a car with unlimited fuel tank capacity. It takes cost[i] liters of gasoline to drive from the ith gas station to the I + 1st gas station. You start from one of the gas stations and start with an empty tank.
If you can drive around the loop, return to the number of the gas station at the time of departure, otherwise return to - 1.
explain:
- If the question has a solution, the answer is the only answer.
- The input arrays are all non empty arrays with the same length.
- All elements in the input array are non negative numbers.
Example 1:
input: gas = [1,2,3,4,5] cost = [3,4,5,1,2] output: 3 explain: From gas station 3(3 indexes)Starting, you can get 4 liters of gasoline. At this time, there is oil in the oil tank = 0 + 4 = 4 Litres of gasoline Drive to No. 4 gas station. There are 4 in the fuel tank at this time - 1 + 5 = 8 Litres of gasoline Drive to No. 0 gas station. There are 8 in the fuel tank at this time - 2 + 1 = 7 Litres of gasoline Drive to No. 1 gas station, and there are 7 in the fuel tank - 3 + 2 = 6 Litres of gasoline Drive to No. 2 gas station. There are 6 tanks at this time - 4 + 3 = 5 Litres of gasoline You need to consume 5 liters of gasoline to drive to gas station 3, which is just enough for you to return to gas station 3. Therefore, 3 can be the starting index.
Example 2:
input: gas = [2,3,4] cost = [3,4,3] output: -1 explain: You can't start from No. 0 or No. 1 gas station because there isn't enough gas for you to drive to the next gas station. We can get 4 liters of gasoline from gas station 2. At this time, there is oil in the oil tank = 0 + 4 = 4 Litres of gasoline Drive to No. 0 gas station, and there are 4 in the fuel tank - 3 + 2 = 3 Litres of gasoline Drive to No. 1 gas station, and there are 3 tanks at this time - 3 + 3 = 3 Litres of gasoline You can't return to gas station 2 because you need 4 litres of gasoline on the return trip, but your tank only has 3 litres of gasoline. Therefore, you can't drive around the loop anyway.
In the one-time traversal method, two conditions need to be met for the vehicle to complete the whole journey:
- The train can drive from station i to i+1.
- The total amount of fuel in all stations should be > = the total fuel consumption of the car.
Then, suppose it is normal from station 0 to station k, and the car runs out of oil when driving to station k+1. At this time, the starting point should be set as k+1 station.
Question 1: why should the starting site be set to k+1?
- Because the oil consumption of station K - > k+1 is too large, the remaining oil of station 0 - > k is not negative. Each station is reduced, some remaining oil will be reduced. Therefore, if the station in front of K is used as the starting station, the remaining oil cannot rush through k+1 station.
Question 2: why is it that if all k+1 - > end can pass normally and rest > = 0, it means that the car can complete the whole journey from k+1 station?
- Because the starting point divides the current path into two parts: A and B. Among them, there must be (1) part a residual oil < 0. (2) The remaining oil in part B is > 0.
- Therefore, no matter how many stations, they can be abstracted into two stations (A and b). (1) Start from station B with full fuel, (2) drive to station a and refuel, (3) drive back to station B.
Key * *: B remaining oil > = a total oil lacking. It must be deduced that the remaining oil of b > = the oil missing from each sub site of site a**
code
public int canCompleteCircuit(int[] gas, int[] cost) {
int curRest = 0, sumRest = 0, start = 0;
for (int i = 0; i < gas.length; i++) {
curRest += gas[i] - cost[i];
sumRest += gas[i] - cost[i];
if (curRest < 0) {
start = i + 1;
curRest = 0;
}
}
return sumRest>=0? start:-1;
}
118. Yanghui triangle
Given a nonnegative integer * numRows, * generates the first numRows of Yang Hui triangle.
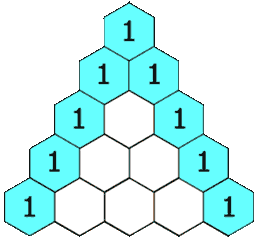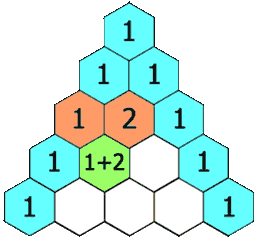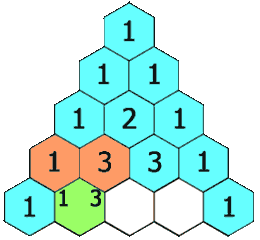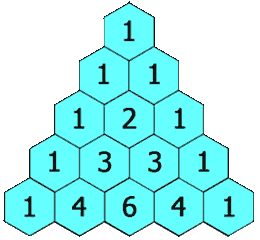
In Yang Hui triangle, each number is the sum of its upper left and upper right numbers.
Example:
input: 5
output:
[
[1],
[1,1],
[1,2,1],
[1,3,3,1],
[1,4,6,4,1]
]
public static List<List<Integer>> generate(int numRows) {
List<List<Integer>> res= new LinkedList<>();
if(numRows == 0) return res;
res.add(Arrays.asList(1));
if(numRows == 1) return res;
List<Integer> lastLine = new LinkedList<Integer>();
for(int i = 2; i<= numRows;i++){
List<Integer> curLine = new LinkedList<>();
curLine.add(1);
for(int j =0;j<lastLine.size()-1;j++){
curLine.add(lastLine.get(j) + lastLine.get(j + 1));
}
curLine.add(1);
res.add(curLine);
lastLine = curLine;
}
return res;
}
Solution I
and 118 questions Similarly, we only need to ask layer by layer. However, you do not need to save the results of each layer. You only need to save the results of the previous layer to find the results of the current layer.
public List<Integer> getRow(int rowIndex) {
List<Integer> pre = new ArrayList<>();
List<Integer> cur = new ArrayList<>();
for (int i = 0; i <= rowIndex; i++) {
cur = new ArrayList<>();
for (int j = 0; j <= i; j++) {
if (j == 0 || j == i) {
cur.add(1);
} else {
cur.add(pre.get(j - 1) + pre.get(j));
}
}
pre = cur;
}
return cur;
}
reference resources here In fact, we can optimize it. We can omit the pre List.
In this way, cur does not create a new List every time, but treats cur as a pre.
Because when updating the current j, the information of the previous J is overwritten. When updating j + 1, we need the information of previous J, so before updating, we need a variable to save the information of previous J.
public List<Integer> getRow(int rowIndex) {
int pre = 1;
List<Integer> cur = new ArrayList<>();
cur.add(1);
for (int i = 1; i <= rowIndex; i++) {
for (int j = 1; j < i; j++) {
int temp = cur.get(j);
cur.set(j, pre + cur.get(j));
pre = temp;
}
cur.add(1);
}
return cur;
}
The difference is that we use the set function to modify the value. Since the current layer has one more element than the previous layer, the element of the last layer will cross the boundary if we use the set method. In addition, the first element of each layer is always 1. Based on these two points, we move the previous case of J = = 0 | J = = I outside the for loop for processing.
In addition to the above optimization idea, there is another idea, that is, reverse it, so there will be no coverage.
Because after updating the information of j, although the information before j is overwritten. But the next time we update j - 1, we need the information of j - 1 and j - 2. The coverage of j information will not be affected.
public List<Integer> getRow(int rowIndex) {
int pre = 1;
List<Integer> cur = new ArrayList<>();
cur.add(1);
for (int i = 1; i <= rowIndex; i++) {
for (int j = i - 1; j > 0; j--) {
cur.set(j, cur.get(j - 1) + cur.get(j));
}
cur.add(1);//Fill in the last 1 of each layer
}
return cur;
}
Solution two formula method
If you are familiar with Yang Hui triangle, you should remember that Yang Hui triangle can actually be regarded as composed of combinatorial numbers.
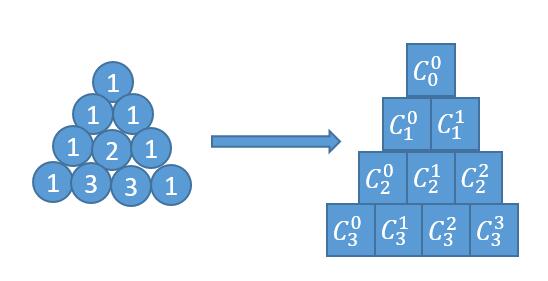
According to the formula of combination number, put (n-k)! Reduction is the result below.
[the external chain picture transfer fails. The source station may have an anti-theft chain mechanism. It is recommended to save the picture and upload it directly (img-wwgxo3e1-1627477036565) (queue. assets/image-20200725110409750.png)]
Then we can use combinatorial numbers to solve the problem.
public List<Integer> getRow(int rowIndex) {
List<Integer> ans = new ArrayList<>();
int N = rowIndex;
for (int k = 0; k <= N; k++) {
ans.add(Combination(N, k));
}
return ans;
}
private int Combination(int N, int k) {
long res = 1;
for (int i = 1; i <= k; i++)
res = res * (N - k + i) / i;
return (int) res;
}
reference resources here , we can optimize it.
In the above algorithm, we recalculate each combination number, but in fact, the combination numbers before and after are related.
[the external chain picture transfer fails. The source station may have an anti-theft chain mechanism. It is recommended to save the picture and upload it directly (img-mmmk3miw-1627477036566) (queue. assets/image-20200725110429884.png)]
Code, we only need to use the pre variable to save the last combination result. During the calculation, the boundary may be exceeded, so long is used.
public List<Integer> getRow(int rowIndex) {
List<Integer> ans = new ArrayList<>();
int N = rowIndex;
long pre = 1;
ans.add(1);
for (int k = 1; k <= N; k++) {
long cur = pre * (N - k + 1) / k;
ans.add((int) cur);
pre = cur;
}
return ans;
}
169. Most elements
The difficulty is simple 674
Given an array of size n, find most of its elements. Most elements refer to elements that appear more than ⌊ n/2 ⌋ in the array.
You can assume that the array is non empty and that there are always many elements in a given array.
Example 1:
input: [3,2,3] output: 3
Example 2:
input: [2,2,1,1,1,2,2] output: 2
Thinking of HashMap
Traverse the entire array and record the number of occurrences of each value (using HashMap, where key is the value and value is the number of occurrences);
Then traverse each Entry in the HashMap to find the value > num The key of length / 2 is sufficient.
class Solution {
public int majorityElement(int[] nums) {
Map<Integer, Long> map = Arrays.stream(nums).boxed().collect(Collectors.groupingBy(Function.identity(), Collectors.counting()));
long limit = nums.length >> 1;
for (Map.Entry<Integer, Long> entry : map.entrySet())
if (entry.getValue() > limit)
return entry.getKey();
return -1;
}
}
Sorting idea
Since there are elements with occurrences > ⌊ n/2 ⌋ in the array, the same elements are always adjacent in the ordered array.
That is, there is a long string of continuous subarrays composed of the same elements with a len gt h of > ⌊ n/2 ⌋.
for instance:
Whether it is 1 1 1 2 3, 0 1 1 1 2 or - 1 0 1 1 1 1, the element in the middle of the array is always "most elements". After all, its len gt h is > ⌊ n/2 ⌋.
class Solution {
public int majorityElement(int[] nums) {
Arrays.sort(nums);
return nums[nums.length >> 1];
}
}
Moore voting method
The candidate (can_num) is initialized to num [0], and the number of votes count is initialized to 1.
When encountered with can_ Num is the same number, then the number of votes count = count + 1, otherwise the number of votes count = count - 1.
When the number of votes count is 0, replace the candidate and reset the number of votes count to 1.
After traversing the array, can_ Num is the final answer.
Why does this work?
The voting method is the same number of votes + 1 and different number of votes - 1.
The number of "most elements" is > ⌊ n/2 ⌋, and the sum of the number of other elements is < = ⌊ n/2 ⌋.
Therefore, the result of the sum of the number of "most elements" - the number of other elements must be > = 1.
This is equivalent to each "majority element" and other elements offsetting each other, and at least one "majority element" must remain in the end.
Whether the array is 1 2 1 2 1, or 1 2 2 1 1, you can always get the right candidate.
class Solution {
public int majorityElement(int[] nums) {
int candidate = nums[0];
int vote = 0;
for(int each : nums){
vote = each == candidate? vote+1 : vote-1;
if(vote<0){
candidate = each;
vote = 1;
}
}
return candidate;
}
}
229. Find mode II
Given an array of size n, find all elements that appear more than ⌊ n/3 ⌋ times.
Note: the time complexity of the algorithm is O(n) and the space complexity is O(1).
Example 1:
input: [3,2,3] output: [3]
Example 2:
input: [1,1,1,3,3,2,2,2] output: [1,2]
Three steps to write code
1. If you vote for A (the current element is equal to A), the number of votes of A is + +;
2. If you vote for B (the current element is equal to b), the number of votes of B is + +;
3. If A and B do not vote (that is, they are not equal to A and B at present), check whether the number of votes of A or B is reduced to 0. If it is 0, the current element becomes A new candidate; If the votes of both candidates A and B are not zero, the votes of both candidates A and B will be reduced by one.
Finally, there are several possibilities: 2 are greater than n/3, 1 is greater than n/3, and 0 is greater than n/3
After the traversal, two candidates are selected, but whether the two candidates meet > n / 3 needs to traverse the array again to find out the specific number of votes of the two candidates, because the title is not like question 169, which is guaranteed.
class Solution {
public List<Integer> majorityElement(int[] nums) {
List<Integer> res = new ArrayList<>();
if (nums == null || nums.length == 0) {
return res;
}
// Define two candidates and their votes
int cand1 = 0,cand2 = 0;
int cnt1 = 0, cnt2 = 0;
// Voting process
for (int num : nums) {
// In case of candidate 1, number of votes++
if (num == cand1) {
cnt1++;
// Traverse again. If you don't want to write continue, you can write multiple else if
continue;
}
// In the case of candidate 2, the number of votes++
if (num == cand2) {
cnt2++;
continue;
}
// It is neither cand1 nor cand2. If cnt1 is 0, it will do cand1
if (cnt1 == 0) {
cand1 = num;
cnt1++;
continue;
}
// If the number of cand1 is not 0 but the number of cand2 is 0, he will do cand2
if (cnt2 == 0) {
cand2 = num;
cnt2++;
continue;
}
// If the number of cand1 and cand2 is not 0, then both are - 1
cnt1--;
cnt2--;
}
// Check that the two votes do not match
cnt1 = cnt2 = 0;
for (int num : nums) {
if (num == cand1) {
cnt1++;
} else if (num == cand2) {
// You must use else if here
// Because the use case of [0,0,0] may appear, the two cand s are the same, and the result of writing two if becomes [0,0]
cnt2++;
}
}
int n = nums.length;
if (cnt1 > n / 3) {
res.add(cand1);
}
if (cnt2 > n / 3) {
res.add(cand2);
}
return res;
}
}
274. H index
Given an array of times a researcher's paper is cited (the number of times cited is a non negative integer). Write a method to calculate the researcher's h index.
Definition of h index : H stands for "high citations". The h index of a scientific researcher refers to that a total of H papers (among n papers) have been cited at least h times. (each of the remaining N - h papers is cited no more than h times.)
For example, a person's h-index is 20, which means that in his published papers, there are 20 papers that have been cited at least 20 times.
Example:
Input: citations = [3,0,6,1,5]
Output: 3
Explanation: a given array indicates that the researcher has a total of 5 papers, and each paper has been cited 3, 0, 6, 1, 5 Times.
Since three papers of the researcher have been cited at least three times, and the other two papers have been cited no more than three times, she h The index is 3.
**Tip: * * if h has multiple possible values, h index is the largest one.
[the external chain picture transfer fails. The source station may have an anti-theft chain mechanism. It is recommended to save the picture and upload it directly (img-xefodkuw-1627477036567) (queue. assets/image-20200726090936564.png)]
public static int hIndex(int[] citations) {
if(citations.length ==0) return 0;
Arrays.sort(citations);
int i = 0;
while (i < citations.length && citations[citations.length - 1 - i] > i) {
i++;
}
return i;
}
[the external chain picture transfer fails. The source station may have an anti-theft chain mechanism. It is recommended to save the picture and upload it directly (img-mpjqifme-1627477036567) (queue. assets/image-20200726091010222.png)]
[the external link image transfer fails. The source station may have an anti-theft chain mechanism. It is recommended to save the image and upload it directly (img-hfplljdk-1627477036568) (queue. assets/image-20200726091034753.png)]
public class Solution {
public int hIndex(int[] citations) {
int n = citations.length;
int[] papers = new int[n + 1];
// count
for (int c: citations)
papers[Math.min(n, c)]++;
// Find the largest k
int k = n;
for (int s = papers[n]; k > s; s += papers[k])
k--;
return k;
}
}
275. H index II
Given an array of times a researcher's paper is cited (the number of times cited is a non negative integer), the array has been arranged in ascending order. Write a method to calculate the researcher's h index.
Definition of h index : "H" stands for "high citations". A researcher's h index means that a total of H papers (among n papers) have been cited at least h times. (each of the remaining N - h papers is cited no more than h times.) "
Example:
input: citations = [0,1,3,5,6]
output: 3
explain: A given array indicates that the researcher has a total of 5 papers, and each paper is referenced 0, 1, 3, 5, 6 Times.
Since three papers of the researcher have been cited at least three times, and the other two papers have been cited no more than three times, she h The index is 3.
explain:
If there are many possible values of H, the h index is the largest one.
public static int hIndex(int[] citations) {
if(citations.length ==0) return 0;
int left = 0,right = citations.length;
while(left<right){
int mid = (left+right)>>>1;
if(citations[mid]<citations.length-mid )
left = mid+1;
else
right = mid;
}
return citations.length-right;
}
public static int hIndex(int[] citations) {
if(citations.length ==0) return 0;
int left = 0,right = citations.length;
while(left<right){
int mid = (left+right)>>>1;
int value = citations[mid];
int target = citations.length-mid ;
if(value < target )
left = mid+1;
else
right = mid;
}
return citations.length-right;
}
Special attention:
In the binary search element, the mode of closing left, opening right and rounding down can be adopted,
It means that the rightmost element in the interval can never be obtained in the process of finding mid,
If the judgment condition is less than value < target, the left boundary needs to be adjusted to mid+1
The judgment condition is greater than or equal to value > = target, and the right boundary needs to be adjusted to the mid position
Use the combination of less than, greater than or equal to, round down,
217. There are duplicate elements
Given an integer array, determine whether there are duplicate elements.
If any value appears in the array at least twice, the function returns true. Returns false if each element in the array is different.
Example 1:
input: [1,2,3,1] output: true
Example 2:
input: [1,2,3,4] output: false
Example 3:
input: [1,1,1,3,3,4,3,2,4,2] output: true
public boolean containsDuplicate(int[] nums) {
Set<Integer> numsSet = new HashSet<>();
for(int i =0;i<nums.length;i++){
if(numsSet.contains(nums[i]))
return true;
else
numsSet.add(nums[i]);
}
return false;
}
219. Duplicate Element II exists
Given an integer array and an integer k, judge whether there are two different indexes I and j in the array, so that num [i] = num [J], and the absolute value of the difference between I and j is at most K.
Example 1:
input: nums = [1,2,3,1], k = 3 output: true
Example 2:
input: nums = [1,0,1,1], k = 1 output: true
Example 3:
input: nums = [1,2,3,1,2,3], k = 2 output: false
public boolean containsNearbyDuplicate(int[] nums, int k) {
Map<Integer,Integer> numsMap = new HashMap<>();
for(int i= 0;i<nums.length;i++){
if(numsMap.containsKey(nums[i])){
if(Math.abs(numsMap.get(nums[i]) - i)<=k)
return true;
else
numsMap.put(nums[i],i);
}
numsMap.put(nums[i],i);
}
return false;
}
thinking
- Tags: hashes
- Maintain a hash table that always contains at most k elements. When duplicate values occur, it indicates that there are duplicate elements within the K distance
- Each time an element is traversed, it is added to the hash table. If the size of the hash table is greater than k, the first number is removed
- Time complexity: O(n)O(n), nn is the array length
class Solution {
public boolean containsNearbyDuplicate(int[] nums, int k) {
HashSet<Integer> set = new HashSet<>();
for(int i = 0; i < nums.length; i++) {
if(set.contains(nums[i])) {
return true;
}
set.add(nums[i]);
if(set.size() > k) {
set.remove(nums[i - k]);
}
}
return false;
}
}
220. Duplicate element III is present
Medium difficulty 200
In the integer array nums, whether there are two subscripts * I * and * j *, so that the absolute value of the difference between nums [i] and nums [j] is less than or equal to t, and the absolute value of the difference satisfying * I * and * j * is also less than or equal to t ķ .
Returns true if it exists and false if it does not exist.
Example 1:
input: nums = [1,2,3,1], k = 3, t = 0 output: true
Example 2:
input: nums = [1,0,1,1], k = 1, t = 2 output: true
Example 3:
input: nums = [1,5,9,1,5,9], k = 2, t = 3 output: false
Method 2 (binary search tree) [pass]
thinking
- If the elements maintained in the window are ordered, you only need to use binary search to check whether condition 2 is satisfied.
- Using the self balanced binary search tree, the elements in the sliding window can be sorted by insertion and deletion in logarithmic time.
algorithm
The real bottleneck of method 1 is to check whether the second condition is met. It is necessary to scan all elements in the sliding window. So what we need to consider is whether there is a better method than full scan.
If the elements in the window are ordered, two binary searches can find the boundary values of x+tx+t and x-tx − t.
Unfortunately, however, the elements in the window are out of order. Here is a very easy mistake for beginners, that is to maintain the sliding window into an orderly array. Although searching in an ordered array only takes logarithmic time, in order to keep the array in order, we have to do insert and delete operations, which are very inefficient. Imagine if you have an ordered array of kk size when you insert a new element xx. Although the position where this element should be inserted can be found in O(\log k)O(logk) time, it still needs O(k)O(k) time to insert xx into this ordered array. Because you have to move all the elements after the position where the current element should be inserted one bit back. The same is true when you want to delete an element. After deleting the elements with subscript ii, you also need to move all elements after subscript ii forward one bit. Therefore, this approach is no better than method i.
In order to improve the efficiency of the algorithm, we need to introduce a dynamic data structure that supports insertion, search and deletion, that is, self balanced binary search tree. The word self balancing means that after random insertion and deletion of the tree, it will automatically ensure the minimum height of the tree. Why does a tree need self balance? This is because most operations on the binary search tree take time, which is directly related to the height of the tree. You can take a look at the following seriously left biased unbalanced binary search tree.
6
/
5
/
4
/
3
/
2
/
1
Figure 1 A severely left biased unbalanced binary search tree.
Finding an element in the above binary search tree takes linear time complexity, which is the same as the speed of searching in the linked list. Now let's compare the following balanced binary search tree.
4
/ \
2 6
/ \ /
1 3 5
Figure 2 A balanced binary search tree
Assuming that the total number of nodes in this tree is nn, a balanced tree can maintain the height at h = \log nh=logn. Therefore, this tree supports inserting, searching and deleting operations within the time of O (H) = O (\ log n) O (H) = O (log n).
The pseudo code of the whole algorithm is given below:
- Initialize an empty binary search tree set
- For each element x, the entire array is traversed
- Find the minimum number greater than or equal to xx on set, and return true if s - x \leq ts − x ≤ t
- Find the maximum number less than or equal to xx on set, and return true if x - g \leq tx − g ≤ t
- Insert xx in set
- If the size of the tree exceeds kk, the number that was first added to the tree is removed.
- Return false
We regard the minimum number ss greater than or equal to xx as the successor node of xx in the BST. Similarly, we can treat the maximum number gg less than or equal to xx as the successor node of xx in the BST. ss and gg are the closest numbers to xx. Therefore, you only need to check the distance between them and xx to know whether condition 2 is satisfied.
- Java
public boolean containsNearbyAlmostDuplicate(int[] nums, int k, int t) {
TreeSet<Integer> set = new TreeSet<>();
for (int i = 0; i < nums.length; ++i) {
// Find the successor of current element
Integer s = set.ceiling(nums[i]);
if (s != null && s <= nums[i] + t) return true;
// Find the predecessor of current element
Integer g = set.floor(nums[i]);
if (g != null && nums[i] <= g + t) return true;
set.add(nums[i]);
if (set.size() > k) {
set.remove(nums[i - k]);
}
}
return false;
}
Complexity analysis
- Time complexity: O(n \log (\min(n,k)))O(nlog(min(n,k)))
We need to traverse this nn length array. For each traversal, searching, inserting or deleting in the BST takes O(\log \min(k, n))O(logmin(k,n)). - Space complexity: O(\min(n,k))O(min(n,k))
The spatial complexity is determined by the size of BST, and the upper limit of its size is determined by kk and nn.
note
- When the elements in the array are very large, mathematical operations may cause overflow. Therefore, consider using data types that support large numbers, such as long.
- std::set, std::set:: upper in C + +_ Bound and std::set::lower_bound is equivalent to TreeSet, TreeSet::ceiling and TreeSet::floor in Java respectively. The Python standard library does not provide self balancing BST.
Method 3 (barrel) [passed]
thinking
Inspired by bucket sorting, we can use bucket as a window to realize a linear complexity solution.
algorithm
Bucket sorting is a sorting algorithm that disperses elements into different buckets. Then, each bucket is sorted independently with different sorting algorithms. An overview of bucket sorting is as follows:
In the above example, we have 8 unordered integers. Let's first create five buckets, which contain [0,9], [10,19], [20,29], [30,39], [40,49] respectively. Any of the eight elements is in a bucket. For an element with a value of X, the label of its bucket is x/w, where we let w = 10. For each bucket, we use other sorting algorithms to sort separately. Finally, we can get an ordered array by collecting all the elements in the order of the bucket.
Back to this problem, the biggest problem we try to solve is:
- For a given element x, is there an element in the interval [x-t, x+t] in the window?
- Can we complete the above judgment in constant time?
We might as well consider each element as a person's birthday. Suppose you are a new student in the class. Your birthday is one day in March. You want to know whether someone in the class has a birthday less than t=30 days from your birthday. Here, let's assume that every month is 30 days. Obviously, we only need to check all students whose birthdays are in February, March and April.
The reason why we can do this is that we know that everyone's birthday belongs to a bucket. We call this bucket month! The interval range contained in each bucket is t, which can greatly simplify our problem. Obviously, the distance between any two elements that are not in the same bucket or adjacent buckets must be greater than t.
We apply the idea of bucket mentioned above to this problem. We design some buckets so that they contain intervals..., [0,t], [t+1, 2t+1]. We use the bucket as a window, so every time we just need to check the bucket to which xx belongs and the elements in the adjacent bucket. Finally, we can solve the problem of searching in the window in constant time.
Another thing worth noting is that the difference between this problem and bucket sorting is that each bucket only needs to contain at most one element, because if any bucket contains two elements, it means that the two elements are close enough, and then we can get the answer directly. Therefore, we only need to use a hash table labeled bucket serial number.
public class Solution {
// Get the ID of the bucket from element value x and bucket width w
// In Java, `-3 / 5 = 0` and but we need `-3 / 5 = -1`.
private long getID(long x, long w) {
return x < 0 ? (x + 1) / w - 1 : x / w;
}
public boolean containsNearbyAlmostDuplicate(int[] nums, int k, int t) {
if (t < 0) return false;
Map<Long, Long> d = new HashMap<>();
long w = (long)t + 1;
for (int i = 0; i < nums.length; ++i) {
long m = getID(nums[i], w);
// check if bucket m is empty, each bucket may contain at most one element
if (d.containsKey(m))
return true;
// check the nei***or buckets for almost duplicate
if (d.containsKey(m - 1) && Math.abs(nums[i] - d.get(m - 1)) < w)
return true;
if (d.containsKey(m + 1) && Math.abs(nums[i] - d.get(m + 1)) < w)
return true;
// now bucket m is empty and no almost duplicate in nei***or buckets
d.put(m, (long)nums[i]);
if (i >= k) d.remove(getID(nums[i - k], w));
}
return false;
}
}
Complexity analysis
- Time complexity: O(n)
For any of these n elements, we only need to do three searches, one insertion and one deletion in the hash table at most. These operations are of constant time complexity. Therefore, the time complexity of the whole algorithm is O(n).
- Spatial complexity: O*(min(n,k))
The extra space needed depends on the size of the hash table, which is linear with the number of elements it contains. The upper limit of the size of the hash table is determined by both N and K. Therefore, the spatial complexity is O(min(n,*k)).
55. Jumping game
Given an array of nonnegative integers, you are initially in the first position of the array.
Each element in the array represents the maximum length you can jump at that position.
Judge whether you can reach the last position.
Example 1:
input: [2,3,1,1,4] output: true explain: We can jump 1 step from position 0 to position 1, Then jump 3 steps from position 1 to the last position.
Example 2:
input: [3,2,1,0,4] output: false explain: In any case, you will always reach the position with index 3. But the maximum jump length of this position is 0, so you can never reach the last position.
public boolean canJump(int[] nums) {
int farStep=0;
for(int i=0;i<nums.length;i++){
if(i>farStep)
break;
farStep = Math.max(farStep,i+nums[i]);
if(farStep>=nums.length-1)
return true;
}
return false;
}
45. Jumping game II
Given an array of nonnegative integers, you are initially in the first position of the array.
Each element in the array represents the maximum length you can jump at that position.
Your goal is to use the least number of hops to reach the last position of the array.
Example:
input: [2,3,1,1,4]
output: 2
explain: The minimum number of jumps to the last position is 2.
Jump from the subscript 0 to the subscript 1 position, jump 1 step, and then jump 3 steps to the last position of the array.
explain:
Suppose you can always reach the last position of the array.
public int jump(int[] nums) {
int curRange =0,farStep=0,count = 0,i=0;
while(i<nums.length-1){
farStep = Math.max(farStep, i + nums[i]);
if(i == curRange){
curRange = farStep;
count++;
}
i++;
}
return count;
}
Special attention:
**Loop boundary condition: * * because ans will be updated in the for loop, that is, the number of jumps. In this question, it is guaranteed to reach the end point. Even if i == end, if I have reached the end point, I don't need to jump again.
**Initial curRange value: * * should be set to 0 instead of nums[0]
121. The best time to buy and sell stocks
Simple difficulty 1099
Given an array, its i-th element is the price of a given stock on day I.
If you are allowed to complete only one transaction at most (i.e. buy and sell a stock once), design an algorithm to calculate the maximum profit you can make.
Note: you cannot sell stocks before you buy them.
Example 1:
input: [7,1,5,3,6,4]
output: 5
explain: On day 2 (stock price) = 1)When buying, on day 5 (stock price) = 6)When you sell, you make the most profit = 6-1 = 5 .
Note that the profit cannot be 7-1 = 6, Because the selling price needs to be greater than the buying price; At the same time, you can't sell stocks before buying.
Example 2:
input: [7,6,4,3,1] output: 0 explain: under these circumstances, No transaction completed, So the maximum profit is 0.
public int maxProfit(int[] prices) {
int lowPrice=Integer.MAX_VALUE;
int maxProfit = 0;
for(int i=0;i<prices.length;i++){
maxProfit = Math.max(prices[i]-lowPrice,maxProfit);
lowPrice = Math.min(prices[i], lowPrice);
}
return maxProfit;
}
Note: if the price becomes lower, you will certainly not earn more money. You can reduce one judgment
public int maxProfit(int prices[]) {
int minprice = Integer.MAX_VALUE;
int maxprofit = 0;
for (int i = 0; i < prices.length; i++) {
if (prices[i] < minprice)
minprice = prices[i];
else if (prices[i] - minprice > maxprofit)
maxprofit = prices[i] - minprice;
}
return maxprofit;
}
122. The best time to buy and sell stocks II
Given an array, its i-th element is the price of a given stock on day I.
Design an algorithm to calculate the maximum profit you can make. You can complete as many transactions as possible (buying and selling a stock multiple times).
**Note: * * you cannot participate in multiple transactions at the same time (you must sell the previous shares before buying again).
Example 1:
input: [7,1,5,3,6,4]
output: 7
explain: On day 2 (stock price) = 1)When buying, on day 3 (stock price) = 5)Sell at, The exchange is profitable = 5-1 = 4 .
Then, on day 4 (stock price) = 3)When buying, on day 5 (stock price) = 6)Sell at, The exchange is profitable = 6-3 = 3 .
Example 2:
input: [1,2,3,4,5]
output: 4
explain: On day 1 (stock price) = 1)When buying, on day 5 (stock price) = 5)Sell at, The exchange is profitable = 5-1 = 4 .
Note that you can't buy stocks on day 1 and day 2 and then sell them.
Because you are involved in multiple transactions at the same time, you must sell the previous shares before buying again.
Example 3:
input: [7,6,4,3,1] output: 0 explain: under these circumstances, No transaction completed, So the maximum profit is 0.
Tips:
- 1 <= prices.length <= 3 * 10 ^ 4
- 0 <= prices[i] <= 10 ^ 4
Greedy Algorithm
Add positive numbers only
public int maxProfit(int[] prices) {
int sumProfit = 0;
for(int i=0;i<prices.length-1;i++){
sumProfit += prices[i+1]>prices[i] ? prices[i+1]-prices[i] : 0;
}
return sumProfit;
}
123. The best time to buy and sell stocks III
Given an array, its ith element is the price of a given stock on day i.
Design an algorithm to calculate the maximum profit you can make. You can complete up to two transactions.
Note: you cannot participate in multiple transactions at the same time (you must sell the previous shares before buying again).
Example 1:
input: [3,3,5,0,0,3,1,4]
output: 6
explain: On day 4 (stock price) = 0)When buying, on day 6 (stock price) = 3)When sold, the exchange can make a profit = 3-0 = 3 .
Then, on day 7 (stock price) = 1)When buying, on day 8 (stock price) = 4)When sold, the exchange can make a profit = 4-1 = 3 .
Example 2:
input: [1,2,3,4,5]
output: 4
explain: On day 1 (stock price) = 1)When buying, on day 5 (stock price) = 5)Sell at, The exchange is profitable = 5-1 = 4 .
Note that you can't buy stocks on day 1 and day 2 and then sell them.
Because you are involved in multiple transactions at the same time, you must sell the previous shares before buying again.
Example 3:
input: [7,6,4,3,1] output: 0 explain: In this case, No transaction completed, So the maximum profit is 0.
[the external chain picture transfer fails. The source station may have an anti-theft chain mechanism. It is recommended to save the picture and upload it directly (img-8t6r2iap-1627477036569) (queue. assets/image-20200727185618096.png)]
[the external chain picture transfer fails. The source station may have an anti-theft chain mechanism. It is recommended to save the picture and upload it directly (img-dp9rfc1l-1627477036569) (queue. Assets / image-2020072700642519. PNG)]
There are two possible situations in stages 1, 3 and 5:
- I didn't hold any shares yesterday, but I'm holding f[i-1]f[j] shares today
- I held the stock yesterday and just bought it today. I enjoy today's income res[i-1][j-1]+price[i-1]-price[i-2]
Possible situations in stages 2 and 4:
- Yesterday's holding of stocks, today's holding of earnings res[i-1][j]+price[i-1]-price[i-2]
- No stocks yesterday, just bought today, no gains res[i-1][j-1]
- Selling and buying immediately can be equivalent to not selling
If there is no stock in hand on the last day, the maximum value in status 1, 3 and 5 of the last day will be returned
public int maxProfit(int[] price){
int[][] res = new int[price.length+1][6];
res[0][1] = 0;
res[0][2] = res[0][3] = res[0][4] = res[0][5] = Integer.MIN_VALUE;
for(int i = 1;i<=price.length;i++){
for(int j =1;j<=5;j+=2){
res[i][j] = res[i-1][j];
if(i>1&&j>1&&res[i-1][j-1] != Integer.MIN_VALUE)
res[i][j] = Math.max(res[i][j], res[i-1][j-1]+price[i-1]-price[i-2]);
}
for(int j =2;j<=5;j+=2){
res[i][j] = res[i-1][j-1];
if(i>1&&res[i-1][j] != Integer.MIN_VALUE)
res[i][j] = Math.max(res[i-1][j]+price[i-1]-price[i-2],res[i-1][j-1]);
}
}
return Math.max(Math.max(res[price.length][1],res[price.length][3]),res[price.length][5]);
}
Special attention:
- Pay attention to if discrimination conditions to avoid crossing the boundary
- res1 corresponds to the first day, and price0 corresponds to the first day
11. Container containing the most water
Give you n nonnegative integers a1, a2,..., an, each representing a point (i, ai) in the coordinate. Draw n vertical lines in the coordinates. The two endpoints of the vertical line i are (i, ai) and (i, 0). Find the two lines so that the container formed by them and the x-axis can hold the most water.
**Note: * * you cannot tilt the container, and the value of n is at least 2.
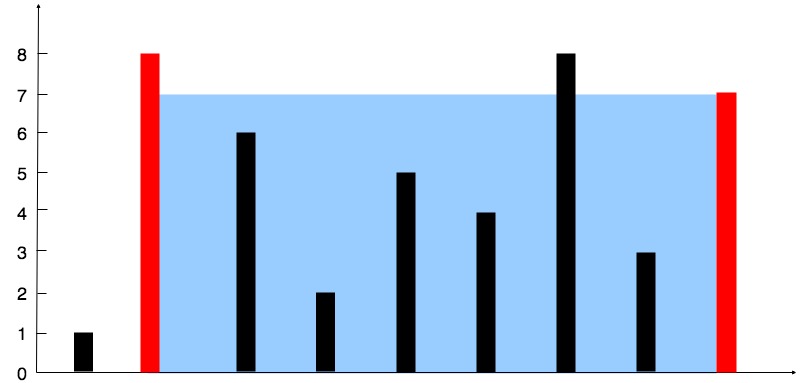
The vertical lines in the figure represent the input array [1,8,6,2,5,4,8,3,7]. In this case, the maximum value that the container can hold water (represented by the blue part) is 49.
Example:
Input:[1,8,6,2,5,4,8,3,7] Output: 49
public int maxArea(int[] height) {
int i=0,j= height.length-1;
int area = 0;
while(i<j){
area = Math.max(area,(j-i) * Math.min(height[i], height[j])) ;
if(height[i]<height[j]){
int left = height[i];
while(i+1<=j){
i++;
if(height[i]>left)
break;
}
}
else{
int right = height[j];
while(j-1>=i){
j--;
if(height[j]>right)
break;
}
}
}
return area;
}
public int maxArea(int[] height) {
int i = 0, j = height.length - 1, res = 0;
while(i < j){
res = height[i] < height[j] ?
Math.max(res, (j - i) * height[i++]):
Math.max(res, (j - i) * height[j--]);
}
return res;
}
int maxArea(vector<int>& height) {
int left = 0, right = height.size()-1;
int area = (right - left)*min(height[right],height[left]);
while(left!= right){
if(height[right]>height[left]) left++;
else right--;
int newArea= (right - left)*min(height[right],height[left]);
area = newArea >area?newArea:area;
}
return area;
}
42. Rainwater connection
Given n non negative integers to represent the height diagram of each column with width 1, calculate how much rain the columns arranged according to this can receive after rain.
[the external chain image transfer fails. The source station may have an anti-theft chain mechanism. It is recommended to save the image and upload it directly (img-dtayapvu-1627477036571) (queue. assets/rainwatertrap.png)]
The above is the height map represented by the array [0,1,0,2,1,0,1,3,2,1,2,1]. In this case, 6 units of rainwater can be connected (the blue part represents rainwater). Thank Marcos for contributing this map.
Example:
input: [0,1,0,2,1,0,1,3,2,1,2,1] output: 6
int trap(vector<int>& height) {
if(height.size()<3) return 0;
int res =0,part=0;
int left = 0,right=height.size()-1;
int pos;
while(left<right-1){
if(height[left]>height[right]){
pos = right -1;
while(height[pos]<height[right]&&pos!= left)
{
res += height[right]-height[pos];
pos--;
}
right = pos;
}
else{//height[left]<=height[right]
pos = left+1;
while(height[pos]<height[left]&&pos!= right){
res += height[left]-height[pos];
pos++;
}
left = pos;
}
}
return res;
}
be careful:
You can't move both pointers from left to right, because you don't know whether the short board is on the left or right
Pay attention to the judgment conditions of large while loops. In order to avoid errors, it is recommended to use range judgment instead of equality judgment
334. Increasing ternary subsequence
Medium difficulty 200 collection sharing switch to English attention feedback
Given an unordered array, judge whether there is an increasing subsequence with length of 3 in this array.
The mathematical expression is as follows:
If such i, j, k exists and 0 ≤ I < J < K ≤ n-1 is satisfied,
Make arr [i] < arr [J] < arr [k], and return true; Otherwise, false is returned.
Note: the time complexity of the algorithm is O(n) and the space complexity is O(1).
Example 1:
input: [1,2,3,4,5] output: true
Example 2:
input: [5,4,3,2,1] output: false
bool increasingTriplet(vector<int>& nums) {
if(nums.size()<3) return false;
int small=INT_MAX, mid=INT_MAX,pos=0;
while(pos<nums.size()){
if(nums[pos]<=small){
small = nums[pos];
}
else if(nums[pos]<=mid){
mid = nums[pos];
}
else return true;
pos++;
}
return false;
}
First, two new variables small and mid are created to save the minimum and intermediate values of the incremental sequence of length 3 required by the topic.
Then, we traverse the array. For each number, we compare it with small and Mid. if it is less than or equal to small, we replace small; Otherwise, if it is less than or equal to mid, replace mid; Otherwise, if it is greater than mid, it means that we have found an incremental array with length of 3!
Question: when the increment sequence with length of 2 has been found, a number smaller than small comes. Why can small be replaced directly? In this way, the relationship between small and mid in the original array is not incremented according to the index?
pos finds a number larger than mid, and at least one number smaller than mid, and returns true directly
pos finds a number smaller than mid and larger than small, and restores the increasing order.
If the current small and mid are [3,5], then another 1 comes. If we don't replace small with 1, then when the next number is 2 and followed by a 3, we can't find the incremental array of [1,2,3]! In other words, we replace the minimum value in order to better update the intermediate value later!
128. Longest continuous sequence
Given an unordered array of integers, find the length of the longest continuous sequence.
The time complexity of the algorithm is O(n).
Example:
input: [100, 4, 200, 1, 3, 2] output: 4 explain: The longest continuous sequence is [1, 2, 3, 4]. Its length is 4.
int longestConsecutive(vector<int>& nums) {
if(nums.empty())return 0;
unordered_set<int> numSet(nums.begin(),nums.end());
int maxLength=1, length=1;
for(int i:numSet){
if(!numSet.count(i-1)){
int j =i+1;
while(numSet.count(j)){
j++;
}
length = j-i;
}
maxLength = maxLength>length? maxLength:length;
}
return maxLength;
}
be careful:
You can set numset find(i)!= numsSet. End() is replaced by numset Count (I) can improve efficiency
Ways to avoid double counting:
- Use set to filter duplicate elements
- If there is an adjacent number smaller than him, it will not be calculated.
After careful analysis of this process, we will find that many unnecessary enumerations are performed. If we know that there is a continuous sequence of x*,x+1,x+2,..., x+y, and we try to match again from x+1, x+2 or x*+y, the result will certainly not be better than the answer starting from enumerating X. therefore, we can skip when we encounter this situation in the outer loop.
So how to judge whether to skip? Because the number x we want to enumerate must have no precursor x − 1 in the array, otherwise according to the above analysis, we will try to match from X − 1. Therefore, we can judge whether to skip every time we check whether x − 1 exists in the hash table.
164. Maximum spacing
Given an unordered array, find out the maximum difference between adjacent elements of the array after sorting.
If the number of array elements is less than 2, 0 is returned.
Example 1:
input: [3,6,9,1] output: 3 explain: The sorted array is [1,3,6,9], Where adjacent elements (3,6) and (6,9) There is a maximum difference between 3.
Example 2:
input: [10] output: 0 explain: The number of array elements is less than 2, so 0 is returned.
explain:
- You can assume that all elements in the array are non negative integers and the values are in the range of 32-bit signed integers.
- Try to solve this problem with linear time complexity and spatial complexity.
[the external chain picture transfer fails. The source station may have an anti-theft chain mechanism. It is recommended to save the picture and upload it directly (img-qzd0mpjg-1627477036571) (queue. assets/image-20200907185702857.png)]
class Solution {
class Bucket{
public:
bool used = false;
int maxval = INT_MIN;
int minval = INT_MAX;
};
public:
int maximumGap(vector<int>& nums) {
if(nums.size()<2)return 0;
int maxNum = *max_element(nums.begin(),nums.end());
int minNum = *min_element(nums.begin(),nums.end());
int BucketSize = nums.size()-1;//Number of digits minus 1 bucket
int BucketRange = (maxNum - minNum)/(BucketSize-1);//BucketSize bucket, BucketSize-1 spacing, calculate the spacing
//Build bucket
vector<Bucket> buckets(BucketSize);
//Barrel loading
for(int i: nums){
int bucketNum = (i -minNum)/BucketRange;
buckets[bucketNum].used =true;
buckets[bucketNum].maxval = max(buckets[bucketNum].maxval,i);
buckets[bucketNum].minval = min(buckets[bucketNum].minval,i);
}
int pre = minNum,res =buckets[0].maxval-pre;//Note the boundary when two elements
//Pay attention to the usage of pre
//Inter bucket element comparison
for(int m = 0;m<BucketSize;m++){
if(buckets[m].used){
res = max(buckets[m].minval-pre,res);
pre = buckets[m].maxval;
}
}
return res;
}
};
287. Look for duplicates
Given an array num containing n + 1 integers, whose numbers are between 1 and n (including 1 and N), it can be seen that there is at least one duplicate integer. Suppose there is only one repeated integer, find the repeated number.
Example 1:
input: [1,3,4,2,2] output: 2
Example 2:
input: [3,1,3,4,2] output: 3
explain:
- The original array cannot be changed (assuming that the array is read-only).
- Only additional O(1) space can be used.
- The time complexity is less than O(n2).
- There is only one duplicate number in the array, but it may appear more than once.
The outer layer uses binary search, and the inner layer uses violence search
As long as the number of elements less than or equal to the median m in the array exceeds m, it indicates that there are duplicate elements in front of (including) the median, otherwise, the search space is reduced by half
int findDuplicate(vector<int>& nums) {
int begin=1,end=nums.size();
while(begin<end){
int mid = (begin+end)>>1;
int sum=0;
for(int i :nums){
if(i<=mid){
sum++;
}
}
if(sum>mid){
end = mid;
}
else{
begin = mid+1;
}
}
return begin;
}
Sword finger Offer 59 - II Maximum number of queues
Medium difficulty 147 collection sharing switch to English attention feedback
Please define a queue and implement the function max_value gets the maximum value in the queue and requires the function max_value,push_back and pop_ The average sharing time complexity of front is O(1).
If the queue is empty, pop_front and max_value needs to return - 1
Example 1:
input: ["MaxQueue","push_back","push_back","max_value","pop_front","max_value"] [[],[1],[2],[],[],[]] output: [null,null,null,2,1,2]
Example 2:
input: ["MaxQueue","pop_front","max_value"] [[],[],[]] output: [null,-1,-1]
To solve the above problem, we just need to remember the next maximum in the queue after the current maximum is out of the queue.
The specific method is to use a double ended queue deque. Each time you join the queue, if the tail element of deque is less than the value * * of the element about to join the queue, all the elements less than value will be out of the queue, and then enter value into the queue; Otherwise, join the team directly.
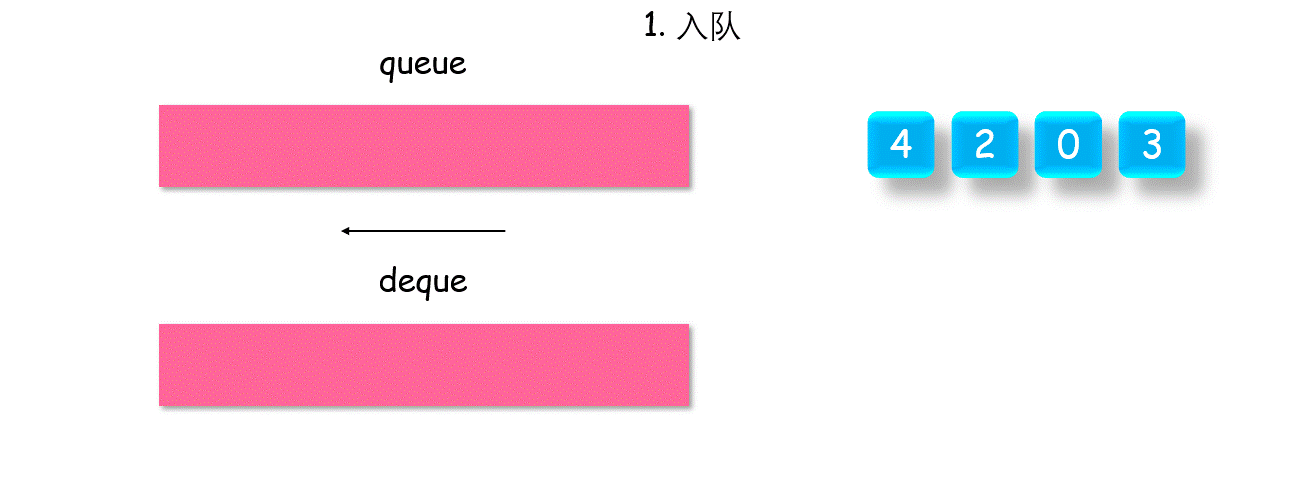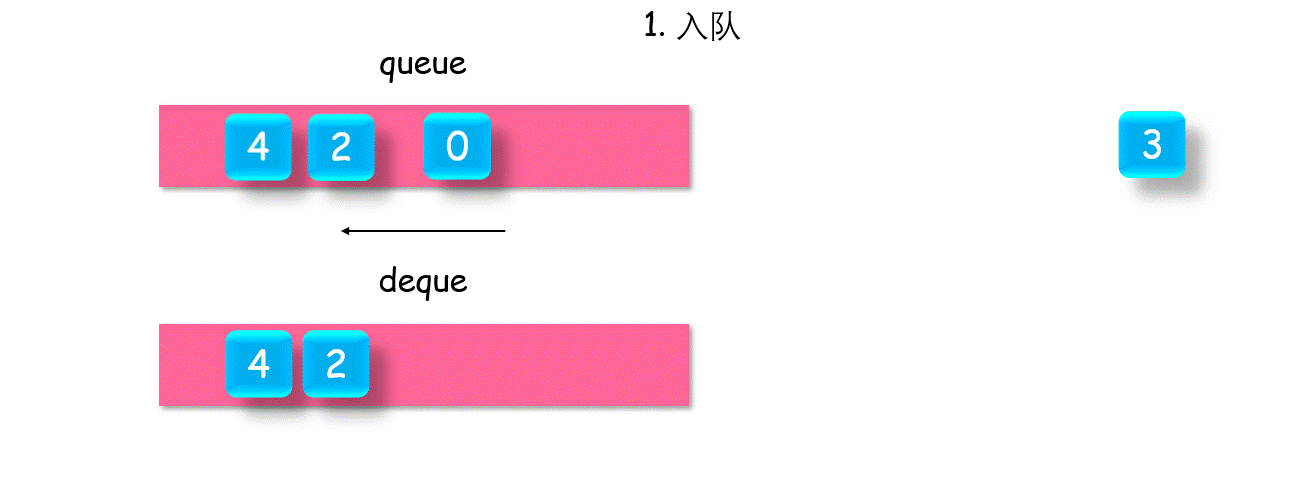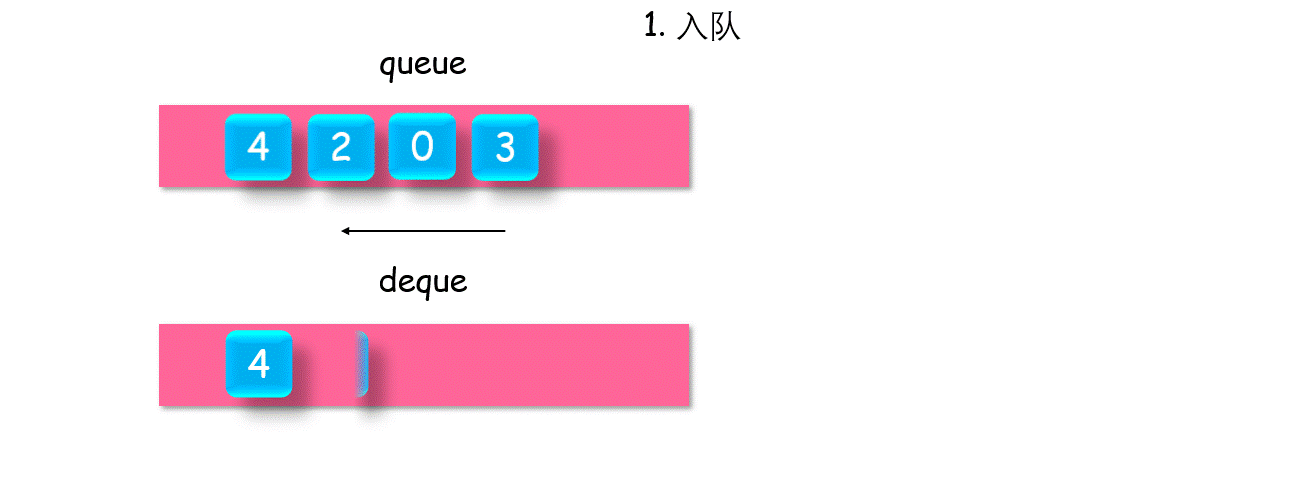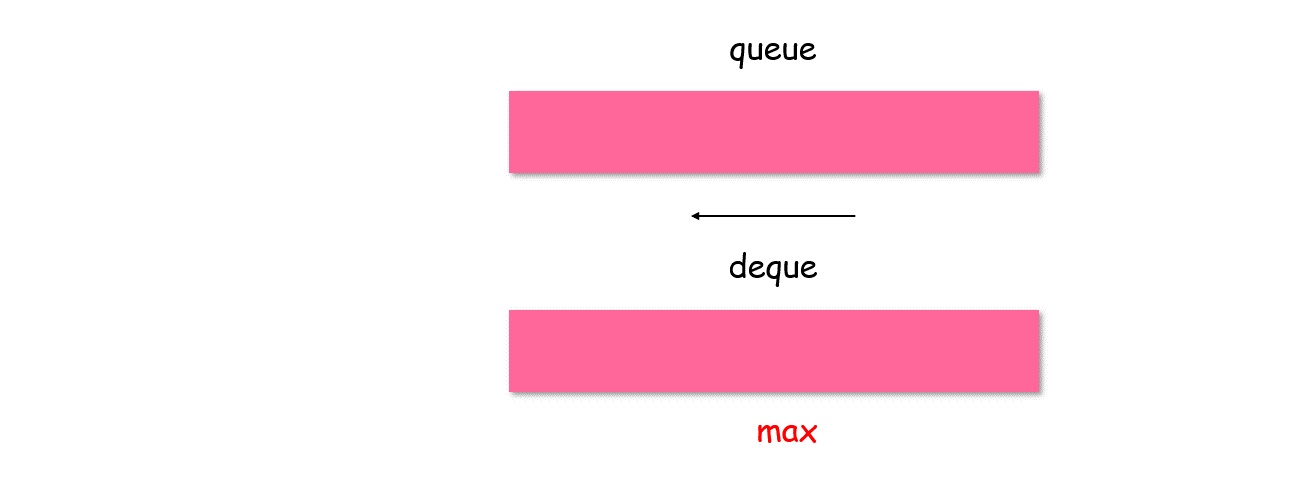
At this time, the first element of the auxiliary queue dequedeque is the maximum value of the queue.
class MaxQueue {
public:
MaxQueue() {
}
queue<int> Que;
deque<int> MaxQue;
int max_value() {
if(Que.empty()) return -1;
return MaxQue.front();
}
void push_back(int value) {
Que.push(value);
if(!MaxQue.empty()&&MaxQue.back()<value){
while(!MaxQue.empty()&&MaxQue.back()<value){
MaxQue.pop_back();
}
}
MaxQue.push_back(value);
}
int pop_front() {
if(Que.empty()) return -1;
int res = Que.front();
if(res==MaxQue.front()){
MaxQue.pop_front();
}
Que.pop();
return res;
}
};
If the number of elements less than or equal to the median m in the group exceeds m, it indicates that there are duplicate elements in front of (including) the median, otherwise, the search space is reduced by half
int findDuplicate(vector<int>& nums) {
int begin=1,end=nums.size();
while(begin<end){
int mid = (begin+end)>>1;
int sum=0;
for(int i :nums){
if(i<=mid){
sum++;
}
}
if(sum>mid){
end = mid;
}
else{
begin = mid+1;
}
}
return begin;
}
Sword finger Offer 59 - II Maximum number of queues
Medium difficulty 147 collection sharing switch to English attention feedback
Please define a queue and implement the function max_value gets the maximum value in the queue and requires the function max_value,push_back and pop_ The average sharing time complexity of front is O(1).
If the queue is empty, pop_front and max_value needs to return - 1
Example 1:
input: ["MaxQueue","push_back","push_back","max_value","pop_front","max_value"] [[],[1],[2],[],[],[]] output: [null,null,null,2,1,2]
Example 2:
input: ["MaxQueue","pop_front","max_value"] [[],[],[]] output: [null,-1,-1]
To solve the above problem, we just need to remember the next maximum in the queue after the current maximum is out of the queue.
The specific method is to use a double ended queue deque. Each time you join the queue, if the tail element of deque is less than the value * * of the element about to join the queue, all the elements less than value will be out of the queue, and then enter value into the queue; Otherwise, join the team directly.
[external chain picture transferring... (IMG oosgwjik-1627477036572)]
At this time, the first element of the auxiliary queue dequedeque is the maximum value of the queue.
class MaxQueue {
public:
MaxQueue() {
}
queue<int> Que;
deque<int> MaxQue;
int max_value() {
if(Que.empty()) return -1;
return MaxQue.front();
}
void push_back(int value) {
Que.push(value);
if(!MaxQue.empty()&&MaxQue.back()<value){
while(!MaxQue.empty()&&MaxQue.back()<value){
MaxQue.pop_back();
}
}
MaxQue.push_back(value);
}
int pop_front() {
if(Que.empty()) return -1;
int res = Que.front();
if(res==MaxQue.front()){
MaxQue.pop_front();
}
Que.pop();
return res;
}
};