Why use quick sort
scene
IP Address query,For example 1000 w strip IP,Your business scenario requires high-frequency data query,return IP address Here, we use linear regression to predict IP Addresses are more efficient than dichotomy ,You don't have to learn the garbage algorithm. Let's go Generally, the query idea is dichotomy, So there are three premises for dichotomy, 1.The data is ordered 2. The elements in the data cannot all be the same 3.Length cannot be 0 with one attached,If there are duplicate elements in the data,Then, even if it is queried, it cannot be ensured that it is the same element The specific implementation idea is 1.take IP 4 zeros of address-255 Convert a decimal number to decimal or binary x1.x2.x3.x4 What is used here is Java language c/c++Fine,Better understanding of bit operations One int Type data takes up 4 bytes and one byte takes up 8 bytes bit Exactly 32 bits , And 0-255 If the range is 256, it is exactly 2^8 The power in binary is 8 bit storage,Each number occupies 8 digits The four numbers are 32,Exactly the same size as int Type memory usage is consistent,int Type representation range is -2147483648-2147483647 Directly use bit operation x1 Shift left 3*8 24 position x2 Shift left 2*8 16 position x3 Shift left 1*8 8 position x4 Shift left 0*8 0 position Then make x1+x2+x3+x4 The result is IP Corresponding binary number ,This is called X With a big X,That is, correspondence IP After mapping,It's convenient to start sorting. Of course, when decoding, turn it over and solve the corresponding decimal number 2.Start sorting after processing Using fast sorting can greatly improve the sorting efficiency 3.After sorting, it is persisted or saved in memory 4.Dichotomy query
When the amount of data is large, using these two excellent algorithms can greatly improve the efficiency
Core idea

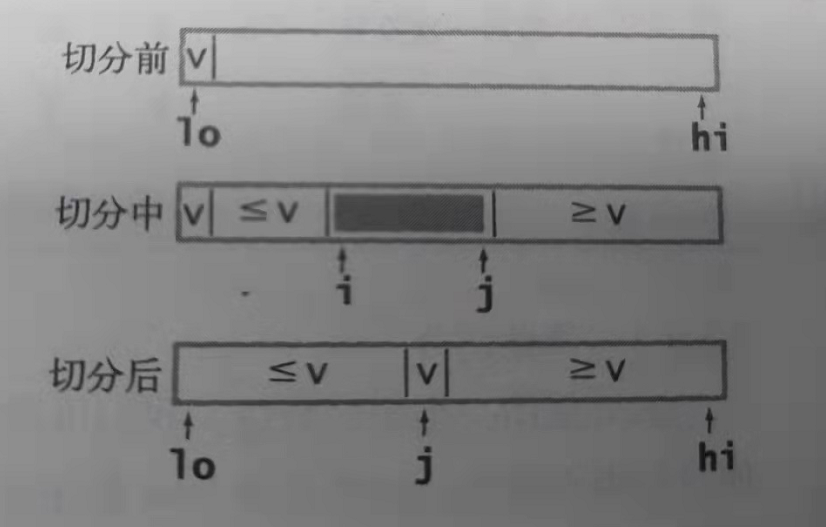
The implementation steps are relatively simple
1. Arbitrarily find a reference value
2. Start from left to right, find the first value greater than or equal to the reference value, and the left pointer stops,
3. Start looking from right to left, find the first value smaller than or equal to the reference value, and the right pointer stops
4. Exchange the left and right reference values and continue the cycle until the left and right pointers are equal. At this time, no value on the left is larger than the reference value and no value on the right is smaller than the reference value. Then you find the position where this element should terminate the cycle. In fact, at this time, the reference value has reached the position where it should exist
5. Recursion between the sequence on the left of the reference value and the sequence on the right of the reference value, and repeat the above steps
6. Stop the loop when the left pointer is greater than or equal to the right pointer under the recursive termination condition
In practice, there is a problem with this idea, that is, there will be infinite recursion when repeated elements exist. At this time, it is necessary to break the cycle. When the left pointer element is equal to the right pointer element, any pointer can be shifted by one bit
The other method is similar. Empty the reference value, find it from the right, write the value to the reference value position after finding the value less than the reference value, and then find it from the left, find the value less than the reference value, write the value to the right pointer position, end the cycle until the two pointers coincide, and write the previous reference value to the pointer coincidence subscript position, Then recurse separately. This method will not encounter the problem of the same element
code implementation
package com.sort;
import java.security.Principal;
public class QuickSort {
/**
* Recursive quick sort
*
* 1.Specify intermediate value
* 2.Compare the middle value from the left and find the one smaller than the middle value
* 3.Start the comparison from the right and find the 4 larger than the middle value. Exchange the element positions of the left and right subscripts
* 5.When exchanging the comparison termination condition start=end, the exact location of mid was found
* 6.Swap the mid element location with the mid element location
* 7.The left and right elements of this mid execute recursion respectively. 8. Left recursion start - (mid-1) right recursion (mid+1) - end
*/
public static void quickSort(int[] arr, int start, int end) {
if (start>end) {
return;
}
//The intermediate variable stores the original position of the pointer
int start_p=start;
int end_p=end;
//1. Specify an intermediate value
int mid=start;
//2 start the comparison cycle
while(start_p< end_p){
//After finding the values of the left and right pointers each time, the position exchange is completed, and the pointer needs to be restored as before
//3 start comparison on the left
if (arr[start_p]==arr[end_p]) {
start_p++;
}
while(arr[start_p]<arr[mid] &&start_p<end_p){
//When a number greater than the reference value is found, and the value is not equal to the right pointer, it can end / / & & arr [start_ p]==arr[end_ p]
start_p++;
}
System.out.print("The subscript of the left pointer of this cycle is:"+start_p);
//Start comparison on the right
while (arr[end_p]>arr[mid] && start_p<end_p ) {
end_p--;
}
System.out.println(" The subscript of the right pointer of this cycle is:"+end_p);
//Exchange position. Before exchanging position, confirm whether the pointer is an element
int tmp=arr[start_p];
arr[start_p]=arr[end_p];
arr[end_p]=tmp;
for (int i = 0; i < arr.length; i++) {
System.out.print(arr[i]+" ");
}
}
for (int i = 0; i < arr.length; i++) {
System.out.print(arr[i]+" ");
}
System.out.println();
//Determine the exact location of mid
int mid_tmp=arr[start_p];
arr[start_p]=arr[mid];
arr[mid]=mid_tmp;
//Start recursion
quickSort(arr, start, start_p-1);
quickSort(arr, start_p+1, end);
}
/**
* Start on the right
* @param arr
* @param start
* @param end
*/
public static void quickSort2(int[] arr, int start, int end) {
if (start>end) {
return;
}
//The intermediate variable stores the original position of the pointer
int start_p=start;
int end_p=end;
//1. Specify an intermediate value
int mid=start;
//2 start the comparison cycle
while(start_p< end_p){
//After finding the values of the left and right pointers each time, the position exchange is completed, and the pointer needs to be restored as before
//3 start comparison on the left
if (arr[start_p]==arr[end_p]) {
start_p++;
}
while (arr[end_p]>arr[mid] && start_p<end_p ) {
end_p--;
}
System.out.println(" The subscript of the right pointer of this cycle is:"+end_p);
while(arr[start_p]<arr[mid] &&start_p<end_p){
//When a number greater than the reference value is found, and the value is not equal to the right pointer, it can end / / & & arr [start_ p]==arr[end_ p]
start_p++;
}
System.out.print("The subscript of the left pointer of this cycle is:"+start_p);
//Start comparison on the right
//Exchange position. Before exchanging position, confirm whether the pointer is an element
int tmp=arr[start_p];
arr[start_p]=arr[end_p];
arr[end_p]=tmp;
for (int i = 0; i < arr.length; i++) {
System.out.print(arr[i]+" ");
}
}
for (int i = 0; i < arr.length; i++) {
System.out.print(arr[i]+" ");
}
System.out.println();
//Determine the exact location of mid
int mid_tmp=arr[start_p];
arr[start_p]=arr[mid];
arr[mid]=mid_tmp;
//Start recursion
quickSort(arr, start, start_p-1);
quickSort(arr, start_p+1, end);
}
public static void main(String[] args) {
int arr[]={6,2,6,2,932,5,123,10,932 };
for (int i = 0; i < arr.length; i++) {
System.out.print(arr[i]+" ");
}
quickSort2(arr, 0, arr.length-1);
// quickSort(arr, 0, arr.length-1);
System.out.println();
for (int i = 0; i < arr.length; i++) {
System.out.print(arr[i]+" ");
}
}
}
Algorithm evaluation
Time complexity
Best case
The best case is that when the array is completely unordered, each benchmark value is selected in the middle, so the number of recursion is the least. Similar to the dichotomy, the time complexity is 1.39NlgN
Average situation
When the array is completely out of order, each benchmark value falls in the whole array according to the normal distribution, then the average time complexity of the algorithm is 2NlgN
Worst case scenario
There are two worst cases. The first is that the array is ordered, so each knife is cut at the edge, and its time complexity is approximately N*N
The second is that the array is completely disordered, but each knife is cut on the edge. Its time complexity is the same as N*N. It is a two-layer cycle like bubble insertion
The additional space used by spatial complexity O(1) is independent of the scale of the problem
So how about the performance of fast platoon?
The average situation of fast scheduling is 39% more than the best situation, so only 11% of the performance is lost, which can effectively solve the problems in most scenarios, which is enough to illustrate the comprehensiveness of this algorithm
Algorithm tuning
Train of thought 1
A known conclusion: when a large number of small arrays are generated in fast scheduling calculation, the performance of some algorithms will be affected
So how to better solve this problem?
Practice has proved that when the length of small array is between 5-15, the effect of insert sorting will be very good
Well, after knowing the conclusion, I found out how to deduce it, but it seems that no one will explain this problem. This is obviously a mathematical problem, probability theory
Trying to prove
Reverse thinking
1. Evaluation of insertion sorting algorithm:
Best case O(N)
Worst case O(N*N)
Average O(N*N)
On average, half of the elements in A[1... j-1] are less than A[j] and half are greater than A[j]. The average running time of insertion sort is the same as the worst-case running time, which is a quadratic function of the input scale [1].
When the group edge of an element in insertion sort is smaller than it and the right side is larger than it, its time complexity remains the same, and this is exactly the order situation that quick sort is most afraid of. This situation will cause the time complexity of quick sort to be N*N, just like the worst case of insertion sort
So what are the benefits if we switch to insert sort?
If the small array is already ordered, the complexity of insertion and sorting is linear. Look at the blue part in the figure
Efficiency ratio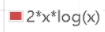
Quick sort high
2. Having explained the advantages of insertion sorting, this paper attempts to explore how the interval [5-15] is calculated
The simplest idea is to make the insertion worst-case time complexity equal to the Quicksort worst-case time complexity
From the image, part of the insertion sorting parabola is lower than the fast arranged curve, but obviously the intersection is less than 5, so it is basically impossible to prove the conclusion here
3. If this is not enough, we can only consider the problem from a practical point of view. The algorithm complexity ignores low-order influencing factors. This neglect is insensitive when the problem scale is large, but when the order of magnitude is small, the problem often occurs because the problem scale is small, even if we compare it more once in each cycle, Will seriously affect performance. Let's take a look at the code for inserting sorting
public static void insertsort(int[] array){
//array[0] as sentinel item
int i,j=0;
for(i=2;i<array.length;i++){
if(array[i]<array[i-1]){
array[0] = array[i];
array[i] = array[i-1];
for(j=i-2;array[j]>array[0];j--){
array[j+1] = array[j];
}
array[j+1] = array[0];
array[0] = 0;
}
}
}
Insert sort: Number of cycles N\*N Comparison times N\*N Assignment times N\*N\*3+N Quick sort Number of cycles N\*N Comparison times N\*N\*4+N Assignment times 2 N\*N+3logN+3N Insert sort sum 4 N\*N + N Quick sort plus 7 N\*N+6N+3logN The above estimates are not very accurate here,However, we can see the influence between other neglected magnitudes and,A rough estimate When the scale of calculation is very small,These low orders cannot be ignored,Insert sort is indeed higher than quick sort At the same time, there is a high probability of the best case when the insertion sort is of low order,The orderly situation is fatal to quick sorting.And when the array segmentation is very small,There is a high probability of array ordering,Or local order,This situation is still well understood.So 5-15 How is it calculated? I am too good at calculating the accurate time complexity of each algorithm,Because there is memory read and write,Exchange comparison, etc,If it can be calculated accurately,Then you can get an accurate interval,Then take an integer in the interval
3. When a large number of repeated elements appear in the actual scene, entropy optimal sorting is used
In human words, the array is divided into three parts, which are less than the benchmark value, equal to the benchmark value and greater than the benchmark value. The remaining ideas are the same. Only the elements equal to the benchmark value are inserted, and the corresponding subscript pointer needs to be modified accordingly. However, when recursing again, only the arrays less than the benchmark value and greater than the benchmark value are passed, The array equal to the reference value does not need to be calculated, because after finding the first correct position, no matter how many duplicate elements there are, there is no need to change the position
4. Three sampling and segmentation
Using the median of a small number of elements in the subarray to segment the array is better, but the cost is to calculate the median. When the size is 3, the effect is the best. That is, instead of setting the benchmark value to start, calculate the median of a start-strat+3 array separately, and then segment