Links to the original text: https://blog.csdn.net/danny_idea/article/details/82258367

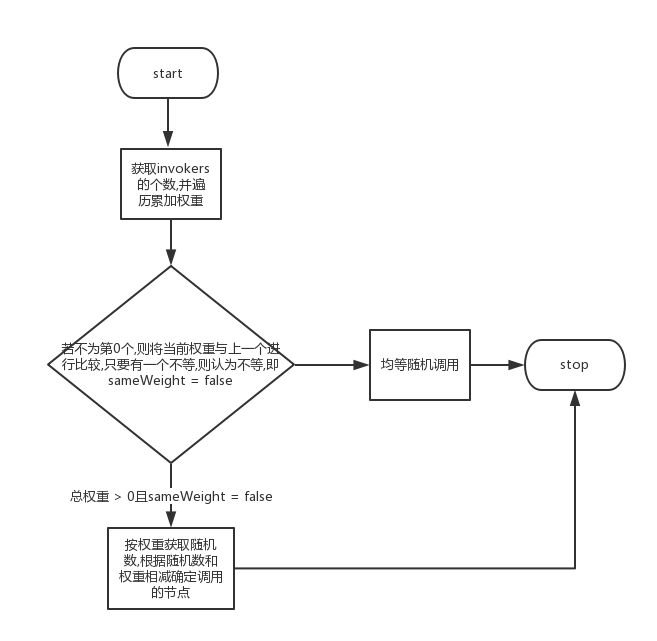
Load balancing in dubbo is implemented by many different algorithms
Random LoadBalance algorithm

public class RandomLoadBalance extends AbstractLoadBalance {
    public static final String NAME = "random";
    private final Random random = new Random();
    protected <T> Invoker<T> doSelect(List<Invoker<T>> invokers, URL url, Invocation invocation) {
        int length = invokers.size(); // Total number
        int totalWeight = 0; // Total weight
        boolean sameWeight = true; // Are the weights the same?
        for (int i = 0; i < length; i++) {
            int weight = getWeight(invokers.get(i), invocation);
            totalWeight += weight; // Cumulative total weight
            if (sameWeight && i > 0
                    && weight != getWeight(invokers.get(i - 1), invocation)) {
                sameWeight = false; // Is the calculation of ownership weight the same?
            }
        }
        if (totalWeight > 0 && ! sameWeight) {
            // If the weights are different and the weights are greater than 0, the total weights are random.
            int offset = random.nextInt(totalWeight);
            // And determine which fragment the random value falls on
            for (int i = 0; i < length; i++) {
                offset -= getWeight(invokers.get(i), invocation);
                if (offset < 0) {
                    return invokers.get(i);
                }
            }
        }
        // If the weights are the same or the weights are zero, then equally random
        return invokers.get(random.nextInt(length));
    }
}


This piece of code may be a little confused when you first look at it, I don't know. offset What's the main function of that parameter? It's just a mathematical design. 

//Specific ideas are shown in the following figure: 


//Assuming that there are three nodes, A,B,C, and then we give them weights of 1, 2, 3, respectively, then we can calculate that the total weight of three nodes is 1 + 2 + 3 = 6, then the access probability of A,B,C is 1/6, 1/3, 1/2, respectively.

So why do we need to get the random number by weight minus the corresponding weight to get the random call node?



 if (totalWeight > 0 && ! sameWeight) {
            // If the weights are different and the weights are greater than 0, the total weights are random.
            int offset = random.nextInt(totalWeight);
            // And determine which fragment the random value falls on
            for (int i = 0; i < length; i++) {
                offset -= getWeight(invokers.get(i), invocation);
                if (offset < 0) {
                    return invokers.get(i);
                }
            }
        }

We can better understand the ideas in this code by drawing graphs: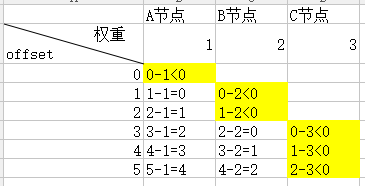

By calculating and counting the weights of A, B and C, when the total weight is 6, the possible value of offset is 0, 1, 2, 3, 4, 5. It is found that when offset is 0, A node will be visited, B node will be visited when offset is 1 and 2, C node will be visited when offset is 3, 4 and 5, and the visiting probability of their three nodes is 1/6, 1/3, 1, 1./ 2. This allocation satisfies our previous weight ratio of 1:2:3.