Recognize stacks and queues
What is stack, JVM virtual machine stack and stack frame? ✌️
- Stack: a linear table with limited operation, which is limited to linear tables with insertion and deletion operations only at the end of the table. This end is called the top of the stack, and the other end is called the bottom of the stack. Inserting a new element into a stack is also called stack entry, stack entry or stack pressing. It puts the new element above the top element of the stack to make it a new top element; Deleting an element from a stack is also called out of stack or out of stack. It deletes the top element of the stack and makes its adjacent elements become new top elements.
- JVM virtual machine stack: a memory area in the JVM. This memory is generally used to store local variables. It is called stack because it has the characteristics of stack: first in and last out.
- Stack frame: in C language, each stack frame corresponds to an unfinished function. The return address and local variables of the function are saved in the stack frame. The memory opened for the function when calling the function is called stack frame, which belongs to the JVM virtual machine stack.
How to use stack? 🍼
-
One kind of multiple-choice questions is to examine the order of entering and leaving the stack. For example, if the sequence of entering the stack is a, b, c, d and e, what is the impossible output sequence of leaving the stack?
A:edcba
B:decba
C:dceab
D:abcde
The first letter of the stack determines that all letters before this letter should have been put into the stack. For example, A: if the first letter of the stack is e, abcd should have been stored in the stack. The order of the stack from the top of the stack is dcba, plus the first letter, and the overall order of the stack is edcba; For B: enter the stack: abc, D into the stack and then out of the stack, e into the stack and then out of the stack, and then cba out of the stack in turn; For C and D: the same consideration, C is wrong. No more details.
-
Infix expression to suffix expression
Infix expression: a general expression of arithmetic or logic formula. That is, the expressions we usually write are infix expressions.
Suffix expression is also called (inverse Polish): write the operator after the operand.
Prefix expressions are also called (polish): unload operators before operands.
How to turn an infix expression into a suffix expression: add a right bracket after the first number after each operator from left to right, and add a left bracket at the position corresponding to the same level until the whole expression is enclosed. Step 2: move each of the above operators to the right of the first parenthesis until the last operator is moved to the right of the right parenthesis of the whole expression. Finally, remove all parentheses, and the expression at this time is the suffix expression. (prefix expression is similar)
For example: (5 + 4) * 3-2 (this is an infix expression)
5 4 + 3 * 2 - (the result of the above infix expression to suffix expression)
-
Why should we convert infix expression into post (pre) infix expression: because what the computer gets is only a string, and there is no priority of operators in the eyes of the computer, so we must actively control the operation steps of an expression.
-
Give you a suffix expression. How to calculate the value of this suffix expression?
First of all, we need to know that the suffix expression we get is essentially a string, or what the computer gets is a string array. When we use i to traverse the above string, when we encounter numbers, we will put them on the stack. Once we encounter an operator, two elements at the top of the stack will pop up, and the first pop-up element will be located on the right side of the operator, The second pop-up element will be on the left side of the operator, and the calculation result will be re stacked until the string is traversed. The last element out of the stack is the result we require.
What are the functions of Stack in the collection framework 🥇
The icon shows the four commonly used methods.
public class TestDemo {
public static void main(String[] args) {
Stack<String> stack=new Stack<>();
//Stack pressing
stack.push("hehe");
stack.push("xixi");
//Out of stack
String ret=stack.pop();//Pop up "xixi"
System.out.println(ret);//Print "xixi"
//Get stack top element
String ret1=stack.peek();//Get "hehe"
System.out.println(ret1);
//Check whether the stack is empty
System.out.println(stack.empty());//false, isEmpty() can also be used here, because the parent class of Stack is
//Vector, the subclass refers to the method called. If there is no definition in the subclass, it will find it in its parent class.
//Find Object o
System.out.println(stack.search("hehe"));//1. The function is to count from the top of the stack to the first Object we want / / to find. If it is not found, it returns - 1
}
}
After learning this, you can do 2 questions:
1: force buckle 150 (evaluated by inverse Polish expression)
2: Sword finger offer31 (press in and pop-up sequence of stack)
You can see the solution in my leetcode column.
View the source code of Stack 🚛
-
When instantiating a Stack object, we can find that there is only one parameterless construct in the Stack class, that is, when we instantiate a Stack object, we can't initialize a capacity for the Stack.
- Observe the fields of the parent class Vector of Stack
protected Object[] elementData;//Like the implementation sequence table we learned before, there is an array protected int elementCount;//Record the number of array elements, which is equivalent to the number of elements in the station
//Nonparametric construction method of Stack: public Stack() { } //We should know that when constructing a subclass, we should first construct the parent class: public Vector() { this(10);//Here is the construction method that calls another parameter in the Vector, as shown below } public Vector(int initialCapacity) { this(initialCapacity, 0);//Here, the construction method of two parameters is called, as shown below } public Vector(int initialCapacity, int capacityIncrement) { super();//Construct the parent class AbstractList if (initialCapacity < 0) throw new IllegalArgumentException("Illegal Capacity: "+ initialCapacity);//A negative stack cannot be initialized this.elementData = new Object[initialCapacity];//Instantiate an Object array this.capacityIncrement = capacityIncrement;//0 }So: from the perspective of source code, the stack is an array.
-
Check the push() capacity expansion mechanism of Stack (similar to the add() capacity expansion mechanism of ArrayList)
//push() source code: E is a generic type that we parameterize. After compilation, it is rubbed into Object public E push(E item) { addElement(item); return item; } //Enter addElement() public synchronized void addElement(E obj) { modCount++;//This can be left alone for the time being ensureCapacityHelper(elementCount + 1);//Make sure there is at least one place in the array where we can insert an element elementData[elementCount++] = obj;//Insert an element at the end and add one to the number of valid elements } //Enter ensureCapacityHelper() private void ensureCapacityHelper(int minCapacity) { // overflow-conscious code if (minCapacity - elementData.length > 0)//Indicates that capacity expansion is required grow(minCapacity);//Specific capacity expansion } //Enter the expansion function grow() private void grow(int minCapacity) { // overflow-conscious code int oldCapacity = elementData.length; //capacityIncrement is the vector overflow (not managed temporarily) int newCapacity = oldCapacity + ((capacityIncrement > 0) ? capacityIncrement : oldCapacity);//It can be seen that the capacity expansion is 2 times, and the add() of ArrayList is 1.5 times if (newCapacity - minCapacity < 0) newCapacity = minCapacity; if (newCapacity - MAX_ARRAY_SIZE > 0) newCapacity = hugeCapacity(minCapacity); elementData = Arrays.copyOf(elementData, newCapacity); }
Self implementation stack 🤙
//Realize the three basic functions of stack: push(), peek(), pop()
public class MyStack {
public int[] elem;
public int usedSize;
public MyStack() {
this.elem = new int[10];//With the source code, the initialization capacity is 10
}
//push()
public void push(int data){
if(isFull()){
this.elem= Arrays.copyOf(this.elem,2*this.elem.length);//2 expanded capacity
}
this.elem[this.usedSize]=data;//Insert an element at the end
this.usedSize++;//Number of valid data plus one
}
private boolean isFull(){
return this.elem.length==this.usedSize;
}
private boolean isEmpty(){
return this.usedSize==0;
}
//For pop(): if the array element type is a reference type, it must be empty to pop up the element, and then the number of valid data is reduced by one. If it is a data type such as int, this is directly usedSize-1
public int pop(){
if(isEmpty()){
throw new RuntimeException("Stack is empty");
}
int oldValue= this.elem[this.usedSize-1];
this.usedSize--;
return oldValue;
}
//peek()
public int peek(){
if(isEmpty()){
throw new RuntimeException("Stack is empty");
}
return this.elem[this.usedSize-1];
}
}
Can we use linked list to realize stack? 🎃
-
If you only want to realize the stack with the help of a linked list, how to do it? We know that the linked list has one-way and two-way. If we use a one-way linked list and press the stack, we need to find the tail of the linked list. The time complexity is O(n), but our goal is to achieve a stack, and the time complexity is best O(1). Let's change our thinking. If the stack is pressed in front of the head node, we find that the time complexity of pressing the stack and leaving the stack is O(1), This is OK.
That is: it is impossible to realize the stack with single chain table tail interpolation, and the time complexity is O (1)
-
At present, the best way to realize the stack with the linked list is to use the two-way linked list. First, press the stack behind the tail node, because our two-way linked list has the last node. Second, the stack can also achieve a time complexity of O(1)
-
First do a few questions, we can know that if we want to use the linked list to realize the stack, we can not only use the single chain header insertion, two-way linked list, but also other methods, because we don't force us to use only one linked list.
- Force buckle 20 (valid brackets) https://leetcode-cn.com/problems/valid-parentheses/
- Force buckle 155 (realize the minimum stack) https://leetcode-cn.com/problems/valid-parentheses/submissions/
queue 🦅
-
Queues are a special kind of Linear table , the special feature is that it only allows deletion at the front of the table and insertion at the back of the table. Like the stack, queue is a linear table with limited operations. The end that performs the insertion operation is called the tail of the queue, and the end that performs the deletion operation is called the head of the queue.
-
View the functions of the Queue interface:
method function boolean add(E) Queue up an element and throw an exception if the queue fails boolean offer(E) Queue up an element. If the queue fails, false will be returned E remove() The team head element is out of the team, and an exception is thrown if it fails to leave the team E poll() The queue header element is out of the queue, and null is returned if out of the queue fails E element() Query the queue header element, and throw an exception if the query fails E peek() Query the queue header element. If the query fails, null is returned -
When viewing the Deque interface, because it implements the Queue interface, it expands the functions of the Queue interface (there is a group at the beginning and end)
[the external chain image transfer fails. The source station may have anti-theft chain mechanism. It is recommended to save the image and upload it directly (img-mp4hy9yi-1643431534780) (C: \ users \ lebronharden \ appdata \ roaming \ typora \ typora user images \ image-20220129113753258. PNG)]
-
For LinkedList, it can be used as an ordinary queue (the bottom layer is a two-way linked list), a double ended queue (the bottom layer is a two-way linked list, of course, can be used as a double ended queue), or itself (a two-way linked list); In short, what is involved here is an interview question: what are the differences between ArrayList and LinkedList?
Queue with linked list 🥂
- First of all, if the single linked list realizes the queue, which head and tail of the linked list will be the head of the queue? If the head node of the linked list is used as the team head: at this time, the time complexity of leaving the team is O(1); The time complexity of joining the team is O(n), because when joining the team, we need to find the tail (the tail node of the linked list); If the reverse is also an O(n) and an O(1), if the queue must be implemented with a one-way linked list, we can take the tail node as a separate field, and each queue operation can directly tail insert a node according to the tail node already recorded, and the queue time complexity is also O(1)
class Node{
public int val;
public Node next;
public Node(int val) {
this.val = val;
}
}
public class MyQueue {
public Node head;
public Node last;
//offer()
public void offer(int data){
Node node=new Node(data);
if(this.head==null){
this.head=node;
this.last=node;
}else{
this.last.next=node;
this.last=node;
}
}
//poll() out of line
public int poll(){
if(isEmpty()){
return -1;
}
int oldValue=this.head.val;
this.head=this.head.next;
return oldValue;
}
private boolean isEmpty(){
return this.head==null;
}
//peek() query queue header element
public int peek(){
if(isEmpty()){
return -1;
}
return this.head.val;
}
}
So far: the bottom layer has realized the queue with a two-way linked list, and we have realized the queue with a single linked list.
Implement queue with array 🚙
-
Factors to consider when implementing queues with arrays:
-
Suppose an array with initialized capacity is regarded as a queue. For example, the position with subscript 0 is the head of the queue and the other end is the tail of the queue. Put several elements in the array (enough to fit), and then perform the operation of poll() out of the queue. The head of the queue turns to the position with subscript 1. After poll() for many times, the array may have many "vacancies" from the position with subscript 0, At the same time, we will offer() again until we put it in the last position of the array. At this time, we can't put it in without capacity expansion. But: some of the first positions of the array are still empty. The above is the so-called false overflow phenomenon.
-
Based on the above phenomenon, in order to make full use of the array, we have to find a way to perform some operations on the index of the array to realize the circulability of the index of the array.
-
The formula of subscript cycle is given based on 2:
When joining the team: (the subscript becomes larger until it overflows. At this time, it should be operated to the position of the small subscript): (index+offset)% array length
When the first subscript goes forward: (index offset + array.length)% array length
-
How to judge whether an array is filled!
-
How to determine whether an array is filled ⚡ ️
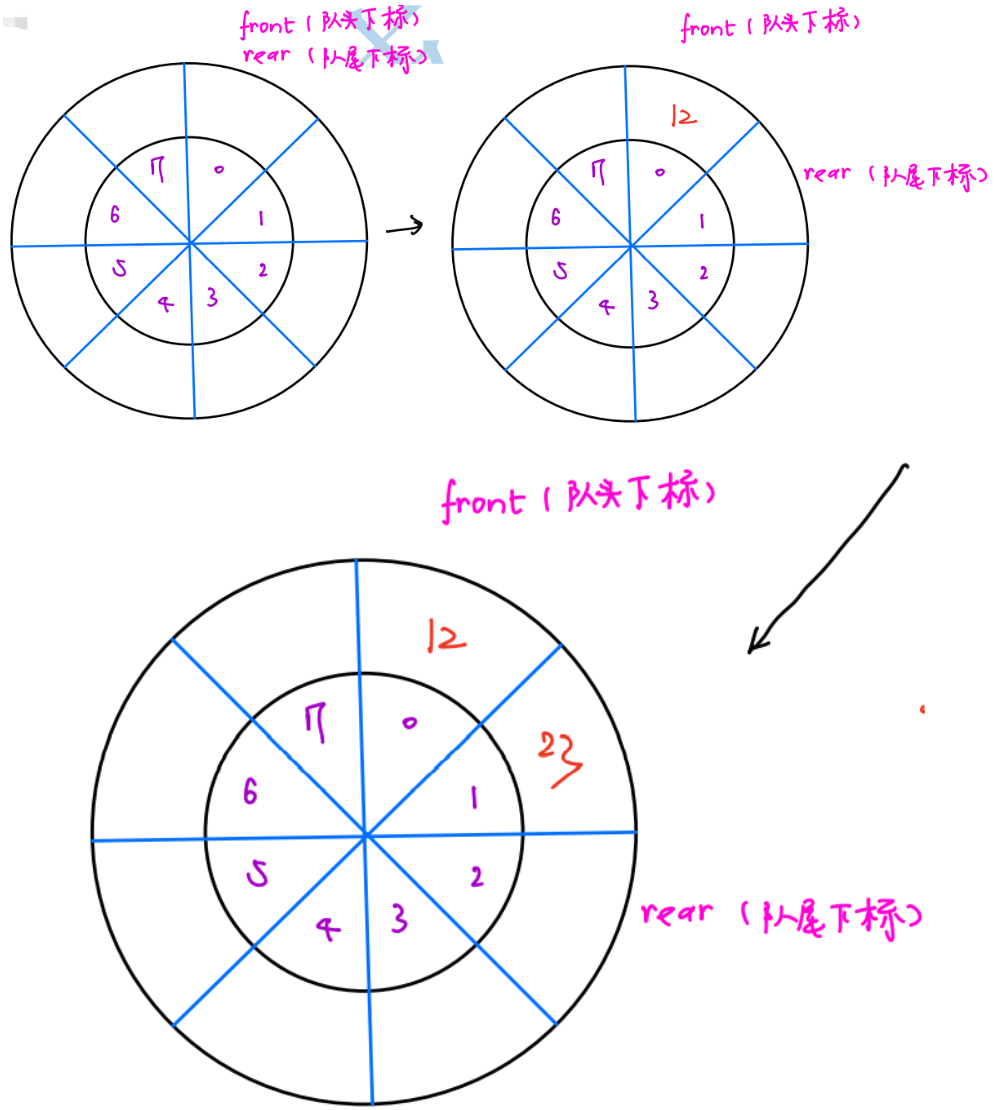
Observation queue operation: rear always records the subscript of the next element.
It is not difficult to find:
- When front and rear meet, they are either empty or full
- How to distinguish between full and empty?
- Method 1: use usedSize. When usedSize is equal to the initialization capacity of the array, the queue slows down
- Method 2: use flag bit: to put it bluntly, define a field flag, and the default is false. Each time you join the team, flag =true; When front ==rear & & Flag = = true, it means that rear has caught up with front. At this time, it is full. On the contrary, it is always flag= false when leaving the team. If front ==rear & & Flag = = false; That is, the array is empty, or the queue is empty. There are four combinations according to whether the front is equal to the rear and whether the flag is true or false. When the front and rear are not equal, the array must not be empty or full, so we will only discuss when the front ==rear.
- Method 3: sacrifice a position to judge whether it is full or not: to put it bluntly, we check whether the next position of the rear is front before putting the element, that is, we don't want to define more fields, but directly use the next front of the rear to judge whether it is full or not, because the rear always records the subscript of the next power element. When the next subscript of the rear is front, We will not put elements, so the last rear will not put elements, so we sacrifice a position.
Design a circular queue ⛈
Li Kou 622 (see my li Kou blog)
Conclusion:
- So far, we know that the bottom layer of the stack is implemented by array, ArrayList is also array (bottom layer) in essence, and LinkedList is a two-way linked list (bottom layer) in essence
- It should be able to realize the stack (array, single linked list and two-way linked list), realize the queue (both single and two-way linked list) and realize the circular queue with circular array. In other words, arrays and linked lists can implement stacks and queues.
- When writing questions, it can be found that the stack and queue also convert to each other. (see my blog)