1, Question type

The input is two one-dimensional arrays, representing the pre / middle / post order traversal and pre / middle / post order traversal results of the tree respectively, and the output is the output binary tree or sequence traversal or others.

2, Classification

　　1. Input: pre sequence + middle sequence} output

　　2. Input: pre sequence + Post sequence output

　　3. Input: middle sequence + rear sequence} output

3, Reconstructed binary tree

　　1. Idea of reconstructing binary tree: the first node of preorder traversal is the root node. After finding the root node in preorder traversal, find the location of the root node in inorder traversal. All points on the left of the root node are its left subtree, and all nodes on the right are its right subtree. Count the number of points in the left subtree, and then look for several points behind the root node in the preorder traversal array. The same is true for the right subtree. Then find the next root node in the left subtree and the right subtree, and repeat the above operation. Combine the following examples to understand.

　　2. Example (pre sequence + middle sequence)

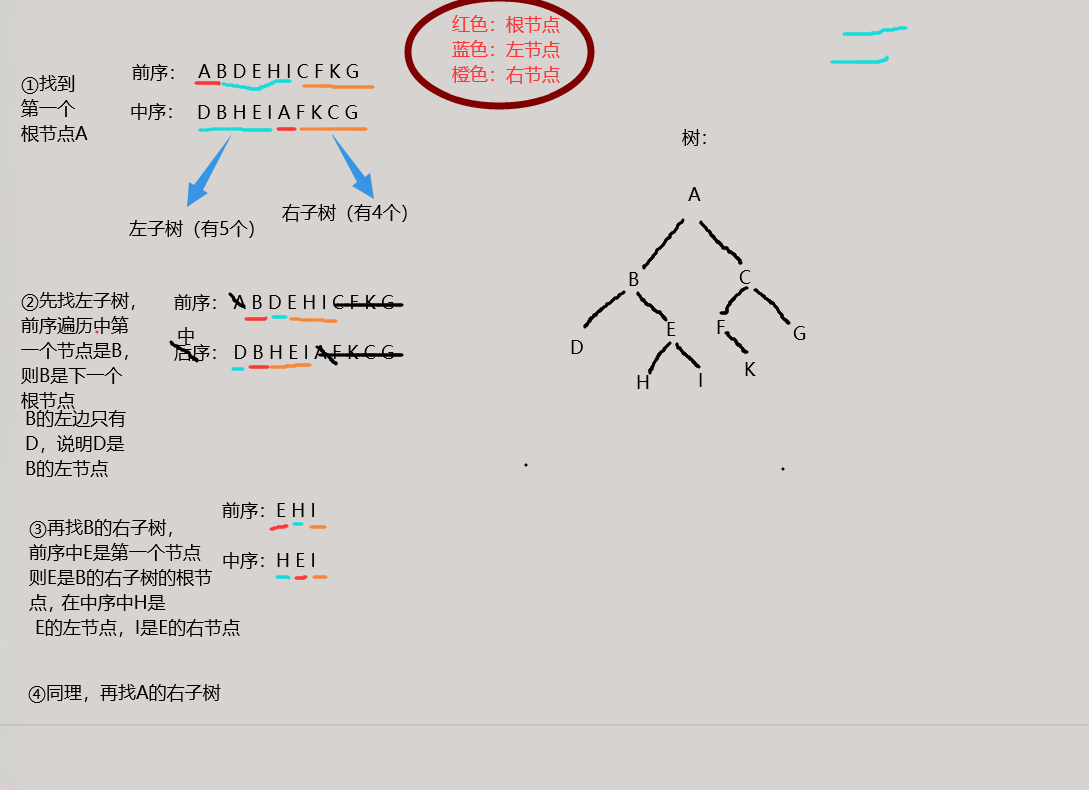
Given the preorder traversal array: preorder: A B D E H I C F K G

Given the middle order traversal array: middle order: D B H E I A F K C G

First, the first node A of the preorder traversal is the root node. Find the position of A in the preorder traversal, and the subscript is 5, then the left 5 nodes of A are the left subtree, and the right 4 nodes are the right subtree.

First recurse the left subtree of A. if there are 5 left subtrees of a, find it within the next 5 ranges of a traversed in the previous order. The first point is B, then B is the first root node of the left subtree, and find the position of B in the middle order, which is 1,

If there is only D on the left of B, then D is the left node of B, and there are three on the right of B, then the right subtree of B is recursive. If there are three points on the right of B, find three points E H I in the preorder traversal. If e comes first, e is the right node of B. Keep repeating....

As shown in the following figure.

　　3. Code framework for reconstructing binary tree

Pre sequence + middle sequence:

#include <bit/sdc++.h>
using namespace std;


int Pre[31],In[31];
typedef struct BinaryTree{
    int key;
    BinaryTree *left;
    BinaryTree *right;
}BinaryTree,*Tree;
//Note: name another one*Tree，It's going to be used in the back queue

//Find the position of the root node of the post order traversal in the middle order traversal, and record it as r
int FindRootInInoder(int begin,int end,int key){
    for(int i=begin;i<end;i++){
        if(key==In[i])
            return i;
    }
}

/**
   Reconstruction of binary tree: preorder + middle order
**/
BinaryTree *GetBinaryTree(int pbegin,int pend,int ibegin,int iend){
//     if(pbegin>=pend || ibegin>=iend){
//         return NULL;
//     }
    BinaryTree *Root = new struct BinaryTree;//Create a new tree
    *Root = {Pre[pbegin],NULL,NULL};   //frontThe first value of the sequence traversal is the root node. be careful: Root There must be before*Otherwise, an error is reported
    int r = FindRootInInoder(ibegin,iend,Pre[pbegin]);
    //Recursively find left subtree and right subtree
    int count=r-ibegin;    //The number of nodes in the left subtree. How many are in the preorder traversal pbegin Start looking for some
    if(r!=ibegin)
        Root->left = GetBinaryTree(pbegin+1, (r-ibegin)+pbegin+1, ibegin, r);
    if(r!=iend)
        Root->right = GetBinaryTree((r-ibegin)+pbegin+1, pend, r+1, iend);
    return Root;
}


int main(){
    int n;
    cin>>n;
    for(int i=0;i<n;i++)
        cin>>Pre[i];
    for(int i=0;i<n;i++)
        cin>>In[i];
    Tree root = GetBinaryTree(0,n-1,0,n-1);//Note: here is n-1 Indexes
    Sequence(root);
    return 0;
}

Middle order + rear order:

The idea and code framework are the same, but the following parts ①, ②, ③ and ④ need to be changed

#include <bit/sdc++.h>
using namespace std;

int Post[31],In[31];
typedef struct BinaryTree{
    int key;
    BinaryTree *left;
    BinaryTree *right;
}BinaryTree,*Tree;
//Note: name another one*Tree，It's going to be used in the back queue

//Find the position of the root node of the post order traversal in the middle order traversal, and record it as r
int FindRootInInoder(int begin,int end,int key){
    for(int i=begin;i<end;i++){
        if(key==In[i])
            return i;
    }
}

/**
   Reconstruction of binary tree: post order + middle order
**/
BinaryTree *GetBinaryTree(int pbegin,int pend,int ibegin,int iend){
//     if(pbegin>=pend || ibegin>=iend){
//         return NULL;
//     }
    BinaryTree *Root = new struct BinaryTree;//Create a new tree
    *Root = {Post[pend],NULL,NULL};   //The last value of post order traversal is the root node. be careful: Root There must be before*Otherwise, an error is reported   ①
    int r = FindRootInInoder(ibegin,iend,Post[pend]);     ②
    //Recursively find left subtree and right subtree
    int count=r-ibegin;    //The number of nodes in the left subtree. How many are in the post order traversal pbegin Start looking for some
    if(r!=ibegin)
        Root->left = GetBinaryTree(pbegin,pbegin+count-1,ibegin,r-1);    ③
    if(r!=iend)
        Root->right = GetBinaryTree(pbegin+count,pend-1,r+1,iend);       ④
    return Root;
}


int main(){
    int n;
    cin>>n;
    for(int i=0;i<n;i++)
        cin>>Post[i];
    for(int i=0;i<n;i++)
        cin>>In[i];
    Tree root = GetBinaryTree(0,n-1,0,n-1);//Note: here is n-1 Indexes
    Sequence(root);
    return 0;
}

Pre sequence + Post sequence: the same, omitted.

4, Examples