Triangle, plane normal, vertex normal
In Direct3D, triangles are the basic units that make up a solid, because a triangle is exactly a plane and rendering efficiency is highest in triangle faces.
A triangle consists of three points, which are traditionally referred to as Vertex. A triangle plane can be divided into positive and negative sides, determined by the order of the vertices: A surface with clockwise vertices is a front, as shown in the figure.
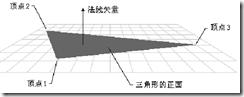
Vectors that are perpendicular to the triangle plane and point to the front are called Normal lines of the plane.
In Direct3D, only the front side is visible by default to improve rendering efficiency.
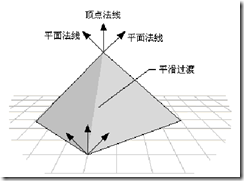
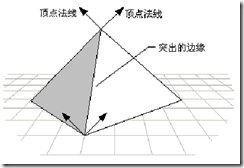
Vertex Normal is a vector that passes through a vertex (normal is a vector) used to calculate illumination and texture effects in Gouraud Shading. When generating a surface, the vertex normal and the normal of the adjacent plane are usually kept at an equal angle, as shown in Figure 1. This renders a smooth transition at the plane seams. If it is a polygon, make the vertex normal equal to the normal of the plane (triangle) to which the point belongs, as shown in Figure 2, to create a prominent edge at the seam.
- In opengl, to simulate light or calculate lighting and shadows, we often need to calculate the normal first. The intensity of light on the surface (i.e. the amount of reflected light) is proportional to the angle between the direction of light and the normal direction, and the smaller the angle, the brighter the surface will look
- To make the surface look smoother, there are two methods. The first is to calculate the normal of eight adjacent vertices, similar to calculating four vertices. The second method is to interpolate normal lines, specifically in shaders. Since most of the time programmable pipes are used, we can use Phong lighting model to transfer the vertex normal lines to the vertex shader, and then interpolate the normal lines in the segment shader to make them look smoother, but the result of this method is not suitable for all models. It looks too bright, and some models need dark colors.
Compute Rotation Matrix
Reference for calculation method of rotation matrix using three Euler angles (should be roll / yaw / pitch) Here
Euler Angle->Rotation Matrix

Rotation Matrix - Euler Angle

Projection Layer (Projects a 3D face onto an image plane)
- Select the focal length and camera location based on experience (generally fixed, Position is the origin, look at direction is -z (in right-hand coordinate system), Up_direction towards y-axis)
Illumination layer
How to view multidimensional matrices
For example, dimensions are (1, 2, 3, 4)
- Looking at the last two numbers, which represent three rows and four columns, you can write them out (assuming the values are all 1)
[[1,1,1,1], [1,1,1,1], [1,1,1,1]]
- When you finish writing the last two dimensions and continue to see that the -3 dimension is 2, then there are 2 3*4 dimensions, which is written as a matrix.
[[[1,1,1,1], [1,1,1,1], [1,1,1,1]], [[1,1,1,1], [1,1,1,1], [1,1,1,1]]]
- Now let's go on to dimension -4, for example, 1, so just add a box and the matrix will be
[[[[1,1,1,1],
[1,1,1,1],
[1,1,1,1]],
[[1,1,1,1],
[1,1,1,1],
[1,1,1,1]]]]
See how a matrix judges dimensions
For example, the following:
[[[[1], [2]], [[3], [4]]]]
- First, the number of front (or last) borders. In the example, there are 4 boxes describing a total of 4 dimensions. Write out the 4 dimensions first (None, None, None)
- Then look for the single box and see that there is only one 1 in the single box, so it is a column. Then there are two single boxes in one box, so there are two lines. So if there are two rows and one column, then the last two dimensions are (2,1), and the total dimension becomes (None, None, 2,1).
- Then look for the double boxes and find that only one comma separates the two pairs of double boxes, so the -3rd dimension is 2 and the total dimension becomes (None, 2, 2, 1).
- Find three boxes at the end and find only one pair of three boxes and no comma-separated three boxes, so the first dimension is 1 and the total dimension is (1, 2, 2, 1)
Practice it
tensor([[[1.0150e+03, 0.0000e+00, 1.1200e+02],
[0.0000e+00, 1.0150e+03, 1.1200e+02],
[0.0000e+00, 0.0000e+00, 1.0000e+00]],
[[1.0150e+03, 0.0000e+00, 1.1200e+02],
[0.0000e+00, 1.0150e+03, 1.1200e+02],
[0.0000e+00, 0.0000e+00, 1.0000e+00]]])
p_matrix = p_matrix.permute(0, 2, 1)
- Here you can see that rows and columns are swapped, which is a bit like transposing in a binary matrix
tensor([[[1.0150e+03, 0.0000e+00, 0.0000e+00],
[0.0000e+00, 1.0150e+03, 0.0000e+00],
[1.1200e+02, 1.1200e+02, 1.0000e+00]],
[[1.0150e+03, 0.0000e+00, 0.0000e+00],
[0.0000e+00, 1.0150e+03, 0.0000e+00],
[1.1200e+02, 1.1200e+02, 1.0000e+00]]])
SH Spherical Harmonic Function
- BRDF (Bidirectional Reflection Distribution Function)
Code
import torch
import math
import numpy as np
from utils import LeastSquares
def split_coeff(coeff):
# input: coeff with shape [1,257]
id_coeff = coeff[:, :80] # identity(shape) coeff of dim 80
ex_coeff = coeff[:, 80:144] # expression coeff of dim 64
tex_coeff = coeff[:, 144:224] # texture(albedo) coeff of dim 80
angles = coeff[:, 224:227] # ruler angles(x,y,z) for rotation of dim 3
# lighting coeff for 3 channel SH function of dim 27
gamma = coeff[:, 227:254]
translation = coeff[:, 254:] # translation coeff of dim 3
return id_coeff, ex_coeff, tex_coeff, angles, gamma, translation
class _need_const:
a0 = np.pi
a1 = 2 * np.pi / np.sqrt(3.0)
a2 = 2 * np.pi / np.sqrt(8.0)
c0 = 1 / np.sqrt(4 * np.pi)
c1 = np.sqrt(3.0) / np.sqrt(4 * np.pi)
c2 = 3 * np.sqrt(5.0) / np.sqrt(12 * np.pi)
d0 = 0.5 / np.sqrt(3.0)
illu_consts = [a0, a1, a2, c0, c1, c2, d0]
origin_size = 300
target_size = 224
camera_pos = 10.0
#Feature face formation model using 3D MM
def shape_formation(id_coeff, ex_coeff, facemodel):
# compute face shape with identity and expression coeff, based on BFM model
# input: id_coeff with shape [1,80]
# ex_coeff with shape [1,64]
# output: face_shape with shape [1,N,3], N is number of vertices
'''
S = mean_shape + \alpha * B_id + \beta * B_exp
'''
n_b = id_coeff.size(0)
face_shape = torch.einsum('ij,aj->ai', facemodel.idBase, id_coeff) + \
torch.einsum('ij,aj->ai', facemodel.exBase, ex_coeff) + \
facemodel.meanshape
face_shape = face_shape.view(n_b, -1, 3)
# re-center face shape
face_shape = face_shape - \
facemodel.meanshape.view(1, -1, 3).mean(dim=1, keepdim=True)
return face_shape
def texture_formation(tex_coeff, facemodel):
# compute vertex texture(albedo) with tex_coeff
# input: tex_coeff with shape [1,N,3]
# output: face_texture with shape [1,N,3], RGB order, range from 0-255
'''
T = mean_texture + \gamma * B_texture
'''
n_b = tex_coeff.size(0)
face_texture = torch.einsum(
'ij,aj->ai', facemodel.texBase, tex_coeff) + facemodel.meantex
face_texture = face_texture.view(n_b, -1, 3)
return face_texture
def compute_norm(face_shape, facemodel):
# compute vertex normal using one-ring neighborhood (8 points)
# input: face_shape with shape [1,N,3]
# output: v_norm with shape [1,N,3]
# https://fredriksalomonsson.files.wordpress.com/2010/10/mesh-data-structuresv2.pdf
# vertex index for each triangle face, with shape [F,3], F is number of faces
face_id = facemodel.tri - 1 #1 is subtracted here because the coordinates start at 0
# adjacent face index for each vertex, with shape [N,8], N is number of vertex
point_id = facemodel.point_buf - 1
shape = face_shape
v1 = shape[:, face_id[:, 0], :]
v2 = shape[:, face_id[:, 1], :]
v3 = shape[:, face_id[:, 2], :]
e1 = v1 - v2
e2 = v2 - v3
face_norm = e1.cross(e2) # compute normal for each face but feel like this refers to calculating the normal of a polygon. It is reasonable to calculate the normal of eight polygons and add them together to get the vertex normal
# normalized face_norm first
face_norm = torch.nn.functional.normalize(face_norm, p=2, dim=2)
empty = torch.zeros((face_norm.size(0), 1, 3),
dtype=face_norm.dtype, device=face_norm.device)
# concat face_normal with a zero vector at the end
face_norm = torch.cat((face_norm, empty), 1)
# compute vertex normal using one-ring neighborhood
v_norm = face_norm[:, point_id, :].sum(dim=2)
v_norm = torch.nn.functional.normalize(v_norm, p=2, dim=2) # normalize normal vectors
return v_norm
def compute_rotation_matrix(angles):
# compute rotation matrix based on 3 ruler angles
# input: angles with shape [1,3]
# output: rotation matrix with shape [1,3,3]
n_b = angles.size(0)
# https://www.cnblogs.com/larry-xia/p/11926121.html
device = angles.device
# compute rotation matrix for X-axis, Y-axis, Z-axis respectively
rotation_X = torch.cat(
[
torch.ones([n_b, 1]).to(device),
torch.zeros([n_b, 3]).to(device),
torch.reshape(torch.cos(angles[:, 0]), [n_b, 1]),
- torch.reshape(torch.sin(angles[:, 0]), [n_b, 1]),
torch.zeros([n_b, 1]).to(device),
torch.reshape(torch.sin(angles[:, 0]), [n_b, 1]),
torch.reshape(torch.cos(angles[:, 0]), [n_b, 1])
],
axis=1
)
rotation_Y = torch.cat(
[
torch.reshape(torch.cos(angles[:, 1]), [n_b, 1]),
torch.zeros([n_b, 1]).to(device),
torch.reshape(torch.sin(angles[:, 1]), [n_b, 1]),
torch.zeros([n_b, 1]).to(device),
torch.ones([n_b, 1]).to(device),
torch.zeros([n_b, 1]).to(device),
- torch.reshape(torch.sin(angles[:, 1]), [n_b, 1]),
torch.zeros([n_b, 1]).to(device),
torch.reshape(torch.cos(angles[:, 1]), [n_b, 1]),
],
axis=1
)
rotation_Z = torch.cat(
[
torch.reshape(torch.cos(angles[:, 2]), [n_b, 1]),
- torch.reshape(torch.sin(angles[:, 2]), [n_b, 1]),
torch.zeros([n_b, 1]).to(device),
torch.reshape(torch.sin(angles[:, 2]), [n_b, 1]),
torch.reshape(torch.cos(angles[:, 2]), [n_b, 1]),
torch.zeros([n_b, 3]).to(device),
torch.ones([n_b, 1]).to(device),
],
axis=1
)
rotation_X = rotation_X.reshape([n_b, 3, 3])
rotation_Y = rotation_Y.reshape([n_b, 3, 3])
rotation_Z = rotation_Z.reshape([n_b, 3, 3])
# R = Rz*Ry*Rx
rotation = rotation_Z.bmm(rotation_Y).bmm(rotation_X)
# because our face shape is N*3, so compute the transpose of R, so that rotation shapes can be calculated as face_shape*R
rotation = rotation.permute(0, 2, 1)
return rotation
def projection_layer(face_shape, fx=1015.0, fy=1015.0, px=112.0, py=112.0):
# we choose the focal length and camera position empirically
# project 3D face onto image plane
# input: face_shape with shape [1,N,3]
# rotation with shape [1,3,3]
# translation with shape [1,3]
# output: face_projection with shape [1,N,2]
# z_buffer with shape [1,N,1]
cam_pos = 10
p_matrix = np.concatenate([[fx], [0.0], [px], [0.0], [fy], [py], [0.0], [0.0], [1.0]],
axis=0).astype(np.float32) # projection matrix
p_matrix = np.reshape(p_matrix, [1, 3, 3])
p_matrix = torch.from_numpy(p_matrix)
gpu_p_matrix = None
n_b, nV, _ = face_shape.size()
if face_shape.is_cuda:
gpu_p_matrix = p_matrix.cuda()
p_matrix = gpu_p_matrix.expand(n_b, 3, 3)
else:
p_matrix = p_matrix.expand(n_b, 3, 3)
face_shape[:, :, 2] = cam_pos - face_shape[:, :, 2]
aug_projection = face_shape.bmm(p_matrix.permute(0, 2, 1))
face_projection = aug_projection[:, :, 0:2] / aug_projection[:, :, 2:]
z_buffer = cam_pos - aug_projection[:, :, 2:]
return face_projection, z_buffer
def illumination_layer(face_texture, norm, gamma):
# CHJ: It's different from what I knew.
# compute vertex color using face_texture and SH function lighting approximation
# input: face_texture with shape [1,N,3]
# norm with shape [1,N,3]
# gamma with shape [1,27]
# output: face_color with shape [1,N,3], RGB order, range from 0-255
# lighting with shape [1,N,3], color under uniform texture
n_b, num_vertex, _ = face_texture.size()
n_v_full = n_b * num_vertex
gamma = gamma.view(-1, 3, 9).clone()
gamma[:, :, 0] += 0.8
gamma = gamma.permute(0, 2, 1)
a0, a1, a2, c0, c1, c2, d0 = _need_const.illu_consts
Y0 = torch.ones(n_v_full).float() * a0*c0
if gamma.is_cuda:
Y0 = Y0.cuda()
norm = norm.view(-1, 3)
nx, ny, nz = norm[:, 0], norm[:, 1], norm[:, 2]
arrH = []
arrH.append(Y0)
arrH.append(-a1*c1*ny)
arrH.append(a1*c1*nz)
arrH.append(-a1*c1*nx)
arrH.append(a2*c2*nx*ny)
arrH.append(-a2*c2*ny*nz)
arrH.append(a2*c2*d0*(3*nz.pow(2)-1))
arrH.append(-a2*c2*nx*nz)
arrH.append(a2*c2*0.5*(nx.pow(2)-ny.pow(2)))
H = torch.stack(arrH, 1)
Y = H.view(n_b, num_vertex, 9)
# Y shape:[batch,N,9].
# shape:[batch,N,3]
lighting = Y.bmm(gamma)
face_color = face_texture * lighting
return face_color, lighting
def rigid_transform(face_shape, rotation, translation):
n_b = face_shape.shape[0]
face_shape_r = face_shape.bmm(rotation) # R has been transposed
face_shape_t = face_shape_r + translation.view(n_b, 1, 3)
return face_shape_t
def compute_landmarks(face_shape, facemodel):
# compute 3D landmark postitions with pre-computed 3D face shape
keypoints_idx = facemodel.keypoints - 1
face_landmarks = face_shape[:, keypoints_idx, :]
return face_landmarks
def compute_3d_landmarks(face_shape, facemodel, angles, translation):
rotation = compute_rotation_matrix(angles)
face_shape_t = rigid_transform(face_shape, rotation, translation)
landmarks_3d = compute_landmarks(face_shape_t, facemodel)
return landmarks_3d
def transform_face_shape(face_shape, angles, translation):
rotation = compute_rotation_matrix(angles)
face_shape_t = rigid_transform(face_shape, rotation, translation)
return face_shape_t
def render_img(face_shape, face_color, facemodel, image_size=224, fx=1015.0, fy=1015.0, px=112.0, py=112.0, device='cuda:0'):
'''
ref: https://github.com/facebookresearch/pytorch3d/issues/184
The rendering function (just for test)
Input:
face_shape: Tensor[1, 35709, 3]
face_color: Tensor[1, 35709, 3] in [0, 1]
facemodel: contains `tri` (triangles[70789, 3], index start from 1)
'''
from pytorch3d.structures import Meshes
from pytorch3d.renderer.mesh.textures import TexturesVertex
from pytorch3d.renderer import (
PerspectiveCameras,
PointLights,
RasterizationSettings,
MeshRenderer,
MeshRasterizer,
SoftPhongShader,
BlendParams
)
face_color = TexturesVertex(verts_features=face_color.to(device))
face_buf = torch.from_numpy(facemodel.tri - 1) # index start from 1
face_idx = face_buf.unsqueeze(0)
mesh = Meshes(face_shape.to(device), face_idx.to(device), face_color)
R = torch.eye(3).view(1, 3, 3).to(device)
R[0, 0, 0] *= -1.0
T = torch.zeros([1, 3]).to(device)
half_size = (image_size - 1.0) / 2
focal_length = torch.tensor([fx / half_size, fy / half_size], dtype=torch.float32).reshape(1, 2).to(device)
principal_point = torch.tensor([(half_size - px) / half_size, (py - half_size) / half_size], dtype=torch.float32).reshape(1, 2).to(device)
cameras = PerspectiveCameras(
device=device,
R=R,
T=T,
focal_length=focal_length,
principal_point=principal_point
)
raster_settings = RasterizationSettings(
image_size=image_size,
blur_radius=0.0,
faces_per_pixel=1
)
lights = PointLights(
device=device,
ambient_color=((1.0, 1.0, 1.0),),
diffuse_color=((0.0, 0.0, 0.0),),
specular_color=((0.0, 0.0, 0.0),),
location=((0.0, 0.0, 1e5),)
)
blend_params = BlendParams(background_color=(0.0, 0.0, 0.0))
renderer = MeshRenderer(
rasterizer=MeshRasterizer(
cameras=cameras,
raster_settings=raster_settings
),
shader=SoftPhongShader(
device=device,
cameras=cameras,
lights=lights,
blend_params=blend_params
)
)
images = renderer(mesh)
images = torch.clamp(images, 0.0, 1.0)
return images
def estimate_intrinsic(landmarks_2d, transform_params, z_buffer, face_shape, facemodel, angles, translation):
# estimate intrinsic parameters
def re_convert(landmarks_2d, trans_params, origin_size=_need_const.origin_size, target_size=_need_const.target_size):
# convert landmarks to un_cropped images
w = (origin_size * trans_params[2]).astype(np.int32)
h = (origin_size * trans_params[2]).astype(np.int32)
landmarks_2d[:, :, 1] = target_size - 1 - landmarks_2d[:, :, 1]
landmarks_2d[:, :, 0] = landmarks_2d[:, :, 0] + w / 2 - target_size / 2
landmarks_2d[:, :, 1] = landmarks_2d[:, :, 1] + h / 2 - target_size / 2
landmarks_2d = landmarks_2d / trans_params[2]
landmarks_2d[:, :, 0] = landmarks_2d[:, :, 0] + trans_params[3] - origin_size / 2
landmarks_2d[:, :, 1] = landmarks_2d[:, :, 1] + trans_params[4] - origin_size / 2
landmarks_2d[:, :, 1] = origin_size - 1 - landmarks_2d[:, :, 1]
return landmarks_2d
def POS(xp, x):
# calculating least sqaures problem
# ref https://github.com/pytorch/pytorch/issues/27036
ls = LeastSquares()
npts = xp.shape[1]
A = torch.zeros([2*npts, 4]).to(x.device)
A[0:2*npts-1:2, 0:2] = x[0, :, [0, 2]]
A[1:2*npts:2, 2:4] = x[0, :, [1, 2]]
b = torch.reshape(xp[0], [2*npts, 1])
k = ls.lstq(A, b, 0.010)
fx = k[0, 0]
px = k[1, 0]
fy = k[2, 0]
py = k[3, 0]
return fx, px, fy, py
# convert landmarks to un_cropped images
landmarks_2d = re_convert(landmarks_2d, transform_params)
landmarks_2d[:, :, 1] = _need_const.origin_size - 1.0 - landmarks_2d[:, :, 1]
landmarks_2d[:, :, :2] = landmarks_2d[:, :, :2] * (_need_const.camera_pos - z_buffer[:, :, :])
# compute 3d landmarks
landmarks_3d = compute_3d_landmarks(face_shape, facemodel, angles, translation)
# compute fx, fy, px, py
landmarks_3d_ = landmarks_3d.clone()
landmarks_3d_[:, :, 2] = _need_const.camera_pos - landmarks_3d_[:, :, 2]
fx, px, fy, py = POS(landmarks_2d, landmarks_3d_)
return fx, px, fy, py
def reconstruction(coeff, facemodel):
# The image size is 224 * 224
# face reconstruction with coeff and BFM model
id_coeff, ex_coeff, tex_coeff, angles, gamma, translation = split_coeff(coeff)
# compute face shape
face_shape = shape_formation(id_coeff, ex_coeff, facemodel)
# compute vertex texture(albedo)
face_texture = texture_formation(tex_coeff, facemodel)
# vertex normal
face_norm = compute_norm(face_shape, facemodel)
# rotation matrix
rotation = compute_rotation_matrix(angles)
face_norm_r = face_norm.bmm(rotation)
# print(face_norm_r[:, :3, :])
# do rigid transformation for face shape using predicted rotation and translation
face_shape_t = rigid_transform(face_shape, rotation, translation)
# compute 2d landmark projection
face_landmark_t = compute_landmarks(face_shape_t, facemodel)
# compute 68 landmark on image plane (with image sized 224*224)
landmarks_2d, z_buffer = projection_layer(face_landmark_t)
landmarks_2d[:, :, 1] = _need_const.target_size - 1.0 - landmarks_2d[:, :, 1]
# compute vertex color using SH function lighting approximation
face_color, lighting = illumination_layer(face_texture, face_norm_r, gamma)
return face_shape, face_texture, face_color, landmarks_2d, z_buffer, angles, translation, gamma