Recursive divide and Conquer - Example 2. Chessboard coverage

1, Problem description

In a chessboard composed of 2^k x 2k squares, exactly one square is incomplete. There are 2(2k) positions of incomplete squares. Therefore, there are 2^(2k) kinds of incomplete chessboard with K ≥ 0
In the problem of chessboard coverage, it is required to cover all squares on the incomplete chessboard with L-shaped dominoes, and any two L-shaped dominoes shall not be overlapped
In the chessboard covering of 2^k x 2k, the number of dominoes used is (4k -1)/3

2, Problem solving ideas

Using divide and conquer algorithm, we can design a simple algorithm to solve the chessboard coverage problem

When k > 0, the 2^k x 2k chessboard is divided into * * four 2(k-1) x 2^(k-1) sub chessboards * *, and the incomplete square must be located in one of the four sub chessboards

There are no incomplete squares in the other three sub chessboards. Therefore, the remaining three chessboards are transformed into incomplete chessboards. An L-shaped dominoes are used to cover the joint of the three smaller chessboards. The squares covered by L-shaped dominoes on the three sub chessboards become the incomplete squares on the chessboard. The original problem is transformed into the chessboard coverage problem of four smaller scales. This segmentation is used recursively until the chessboard is simplified to a 1 x 1 chessboard

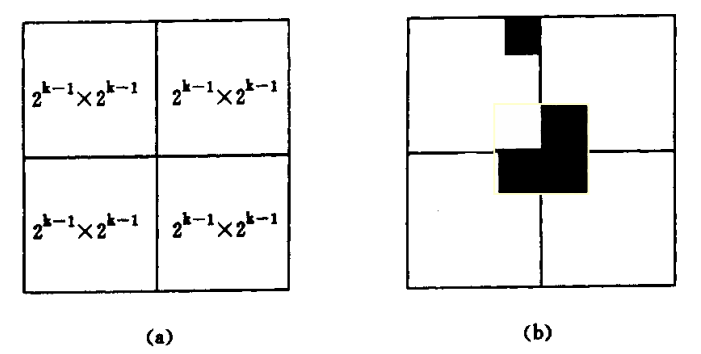
In the code implementation, we use a binary integer array Board to represent the chessboard, and Board[0] [0] is the square in the upper left corner of the chessboard
tile is a global integer variable in the algorithm, which is used to represent the number of L-shaped dominoes. Its initial value is 0. The input parameters of the algorithm are:

• tr: row number in the upper left corner of the chessboard tc: column number in the upper left corner of the chessboard
• dr: row number of the special box dr: column number of the special box
• size: size = 2^k, indicating the size of the chessboard

The code is as follows:

#include<bits/stdc++.h>
using namespace std;
int **Board;
int tile=1; //(0 by default)
void ChessBoard(int tr, int tc, int dr, int dc, int size)
{
    //tr: the row number of the square in the upper left corner of the chessboard tc: the column number of the square in the upper left corner of the chessboard
    //dr: the row number of the special grid dc: the column number of the special grid
    //size: the number of rows or columns of the chessboard
    if(size==1) 
    {
        cout<<"size==1,return!"<<endl;
        return;
    }
    int t = tile++, //Dominoes number, add 1 each time, unify the dominoes number, and the special grid label is 0
    s = size/2;     //Quadrant size, that is, divide the chessboard, and halve the specification each time

    //Cover upper left quadrant
    if(dr<tr+s && dc<tc+s)
        ChessBoard(tr, tc, dr, dc, s);  //The special grid is located in this quadrant
    else 
    {
        //There are no special squares in this quadrant
        Board[tr+s-1][tc+s-1] = t;  //Put the three grid t in the lower right corner and turn this quadrant into a special chessboard
        cout<<"here t:"<<t<<" The grid coordinates are located at:("<<tr+s-1<<","<<tc+s-1<<")"<<endl;
        ChessBoard(tr, tc, tr+s-1, tc+s-1, s);  //Cover the rest
    }

    //Overlay upper right quadrant
    if(dr<tr+s && dc>=tc+s)
        ChessBoard(tr, tc+s, dr, dc, s);  //The special grid is located in this quadrant
    else
    {
        //There are no special squares in this quadrant
        Board[tr+s-1][tc+s] = t;
        cout<<"here t:"<<t<<" The grid coordinates are located at:("<<tr+s-1<<","<<tc+s<<")"<<endl;
        ChessBoard(tr, tc+s, tr+s-1, tc+s, s);  //Cover the rest, and remember to change the coordinates of the upper left corner of the chessboard!
    }
    //Cover lower left quadrant
    if(dr>=tr+s && dc<tc+s)
        ChessBoard(tr+s, tc, dr, dc, s);
    else
    {
        Board[tr+s][tc+s-1] = t;
        cout<<"here t:"<<t<<" The grid coordinates are located at:("<<tr+s<<","<<tc+s-1<<")"<<endl;
        ChessBoard(tr+s, tc, tr+s, tc+s-1, s);  
    }
    // Cover lower right quadrant
    if(dr>=tr+s && dr>=tc+s)
        ChessBoard(tr+s, tc+s, dr, dc, s);
    else
    {
        Board[tr+s][tc+s] = t;
        cout<<"here t:"<<t<<" The grid coordinates are located at:("<<tr+s<<","<<tc+s<<")"<<endl;
        ChessBoard(tr+s, tc+s, tr+s, tc+s, s);
    }
}
void OutputBoard(int size)
{
    for(int i=0; i<size; ++i)
    {
        for(int j=0; j<size; ++j)
        {
            cout.width(5);
            cout<<Board[i][j];
        }
        cout<<endl;
    }
}

int main()
{
    // size: the number of rows or columns of the chessboard
    int size, i;
    cout<<"Lines or Columns of chessBoard: ";
    cin>>size;
    Board = new int*[size];
    for(i=0; i<size; ++i)
    {
        Board[i] = new int[size];
        for(int j=0; j<size; ++j)
            Board[i][j] = 0;
    }

    //dr, dc: the row number and column number of the special square
    int dr, dc;
    cout<<"Line and column NO. of defective grid: ";  //Enter special grid coordinates
    cin>>dr>>dc;
    ChessBoard(0, 0, dr, dc, size);
    OutputBoard(size);
    for(int i=0; i<size; ++i)
        delete[] Board[i];
    delete[] Board;
    system("pause");
    return 0;
}

The following pictures are the results of your class work and the final program:
Test example: chessboard size 8x8, special grid coordinates (3, 5)
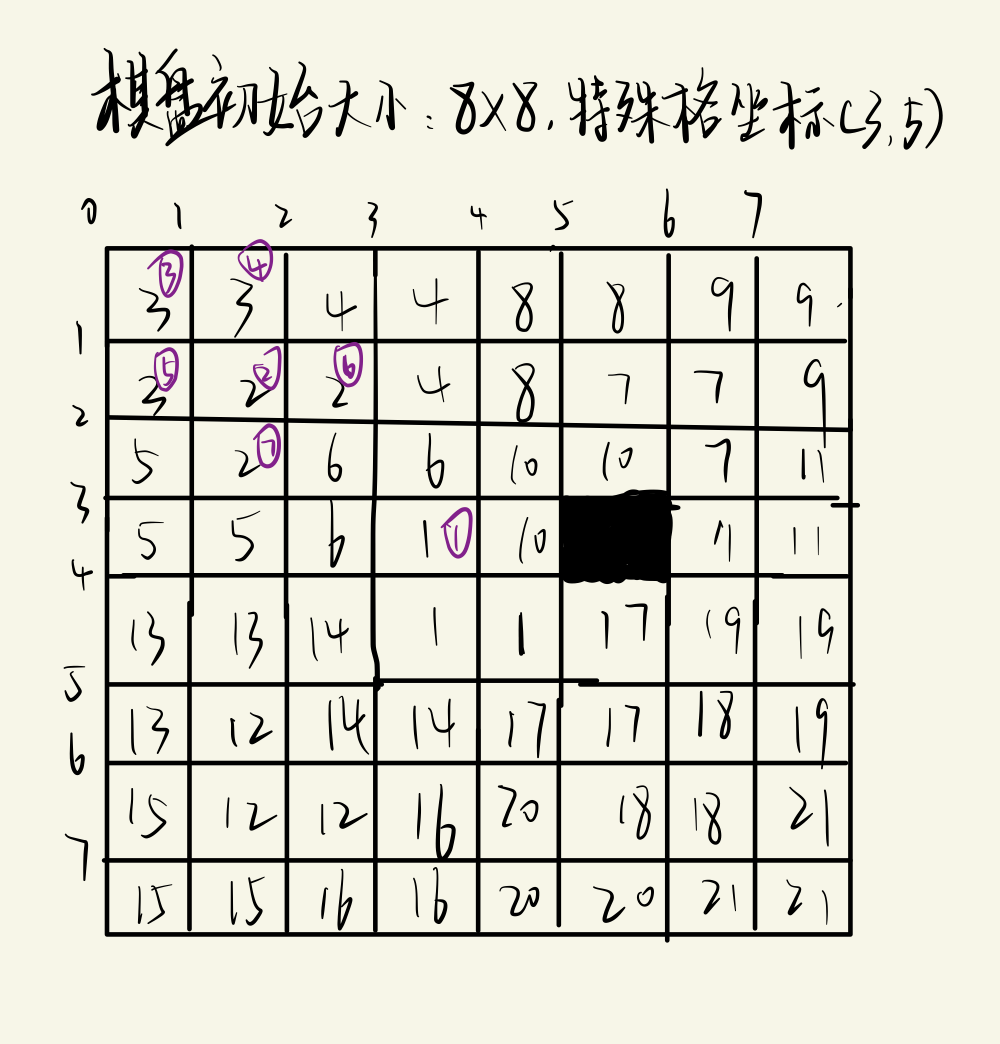The purple sequence number indicates the filling order, which can also be verified by the program
(I seem to have written one wrong, ε=ε=ε= ┏(゜ロ゜;)┛)

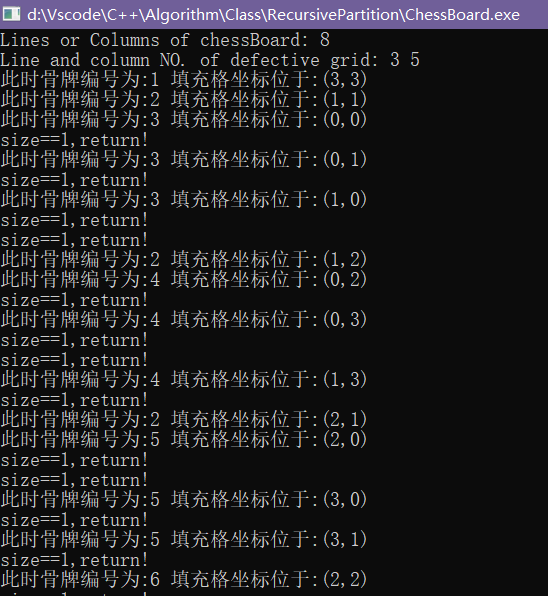
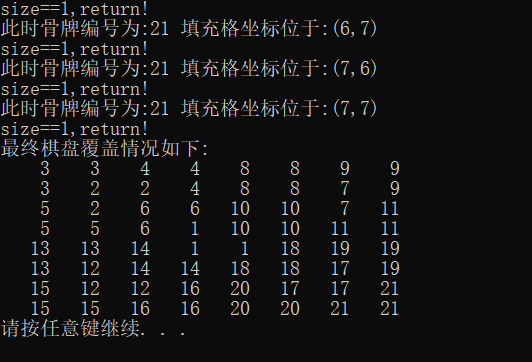
Here's a question that the teacher asked me in class. That's why when recursion comes back, the number of dominoes remains the same
We know that recursion goes all the way in. After the domino number of each layer is + 1, it is saved in the system stack. When the termination condition returns or all the conditions of the current layer return, it will automatically pop up the stack!
This is why we can ensure that the dominoes number of each layer is consistent. There is no doubt about it!

Refer to the courseware of algorithm design and analysis by Mr. Bi Fangming

Welcome to the personal blog website - George's programming cabin , work hard with me for the big factory offer!