If this article is helpful to you, please also 'praise and pay attention', and give me the greatest encouragement to those who are very lost because of the upcoming school.

When I brush the force buckle, I find that it is slightly clumsy to deal with some problems such as double recursion, especially some assignment and condition judgment are interspersed between double recursion. When the state is not good, I even feel timid and dare not touch problems. Think about it and summarize this recursive article.

It's the so-called great road to simplicity. We beginners think recursion is very difficult. The reason is that we just understand it in a hurry at the beginning, write a tired multiplication with the teaching video, or deal with the small homework of beginner programming C language. In this way, we naturally can't meet the requirements of problem solving

The content of this article is very simple and basic, and it is also very suitable for watching in the state of half asleep and half awake. How can a dignified seven foot man cringe because of the difficulty of the algorithm? So don't be afraid.

1, Basic recursion

Instead of talking about the messy principles, let's understand the most basic code:

Case 1: accumulation

Here, for convenience, we do not consider the self assertion of error reporting of non positive integers, but only calculate the range of positive integers, the same below.

def foo(n):
    if n == 1:
        return 1
    return n + foo(n - 1)

Accumulation is undoubtedly 1 + 2 + 3 + 4 +, Assuming n=3, the code here can be regarded as 3 + 2 + 1. Note that only when we finally get to 1, that is, after many times of n-1, can we get the unique return value return 1 of the function. At this time, the innermost layer of the recursive function ends with return 1 and returns to the previous layer return 2+foo(2-1), that is, return 2+1, At this point, you get the result return 3. Return to the first layer return 3 + 3. The final return result is 6

Conclusion: it can be seen from here that this return 1 is particularly important, which is what those video tutorials said at the beginning that there should be a termination condition. If we don't write this return 1, we will report an error. It will tell you that the recursion exceeds the maximum depth.

For beginners, don't think it's easy here. Let's analyze the error code to deepen our understanding:

def foo1(n):
    return n + foo(n - 1)

Although this seems wrong at first glance, we should also think about where it is wrong. Obviously, it is because the infinite foo(n - 1) exceeds the recursion depth limit, and we can see return n +? There is no return value here.

That is: we need a return to 1. Terminate recursion; 2. Get the most basic return value

Of course, we also need something called recurrence. In order to deepen the impression, we will introduce case 2 again.

Exercise 1: tired riding

The same idea as accumulation is to change the plus sign into a multiplication sign. It is suggested that pain Xiaobai knock it again according to the above understanding, rather than complete this simple operation according to the general impression.

def foo(n):
    if n == 1:
        return 1
    return n * foo(n - 1)

Case 2: Fibonacci sequence

The following figure is from Baidu Encyclopedia

We can see that this group of numbers 1, 1, 2, 3, 5, 8, 13 (of course, some start from 0, which doesn't matter)

Here, it gives another key factor of recursion: recursion

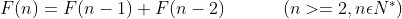
Note: looking back on our previous accumulation, in addition to return 1, there is another step return n + foo(n - 1), which is the recursive formula of our accumulation. The mathematical writing method: F (n) = n + F (n-1) of course requires n > = 1, and it doesn't matter to get 0. It is responsible for the things we need to calculate from large to small, from more to less, from macro to micro, and then subdivide to our minimum element / termination condition. After obtaining the return value, we start from small to large, from less to more, from micro to macro, and add (subtract, multiply and divide) to our final desired result.

For reference accumulation, the code is as follows:

def foo1(n):
    if n <= 1:
        return 1
    return foo1(n - 1) + foo1(n - 2)

Of course, if you think about starting from 0 or taking item 0 instead of item 1, you can make some modifications and learn to be flexible:

def foo2(n):
    if n == 0:
        return 0
    if n == 1:
        return 1
    return foo2(n - 1) + foo2(n - 2)

The operation results are as follows:

for i in range(10):
    print(foo3(i), end=',')
print('')
for i in range(10):
    print(foo4(i), end=',')

#　1,1,2,3,5,8,13,21,34,55,
#　0,1,1,2,3,5,8,13,21,34,

Exercise 2: Yang Hui triangle

There are several questions about Yang Hui's triangle on Li Kou, but I didn't do it with recursive knowledge at that time. Recursion is often the most time-consuming and space-saving method. It often involves the repeated calculation of some sub problems. Therefore, it is often the best to solve it with some knowledge of stack and dynamic programming, and different requirements have different optimal solutions. Nevertheless, we still need to grasp the foundation.

... It's a little far away. Let's learn basic recursion first.

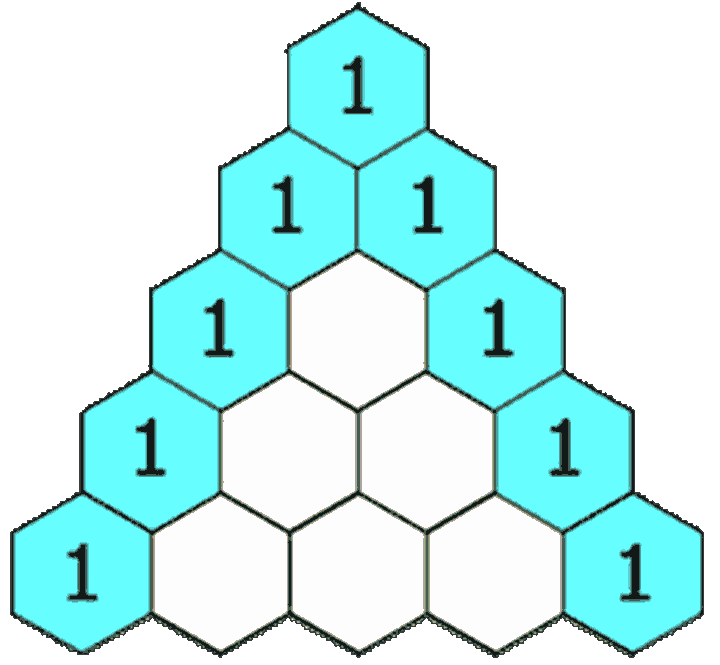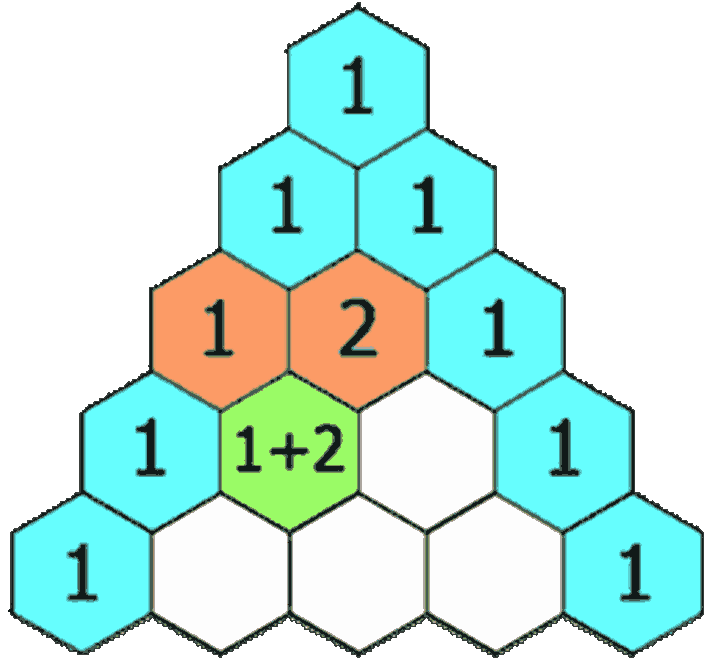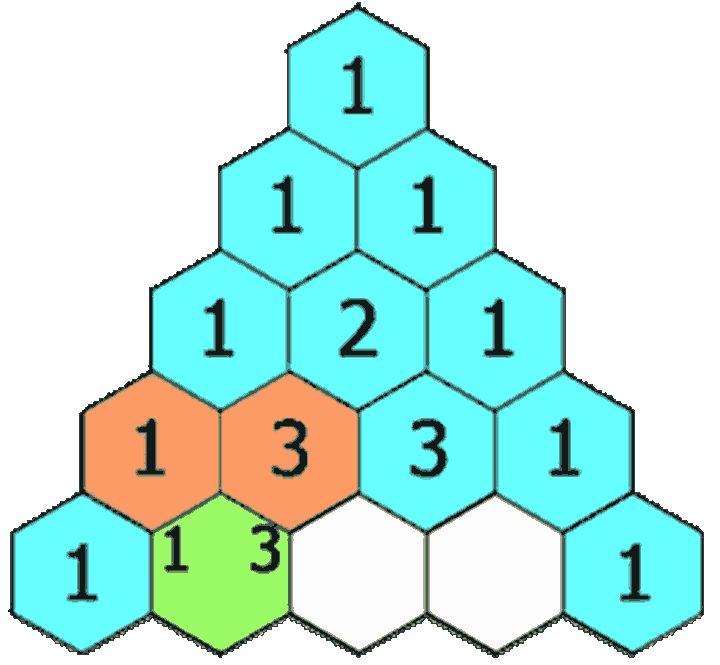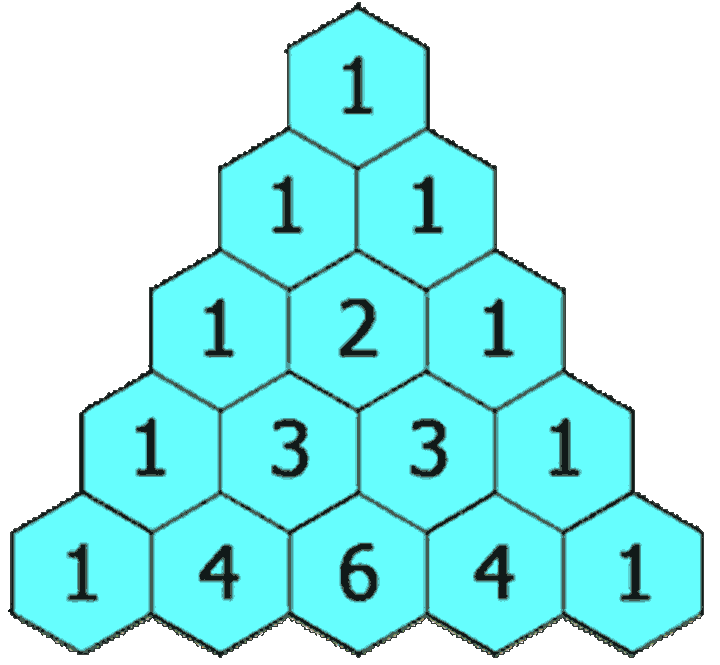
We might as well define it this way, but his recursive formula:

For its I row and j column (I + J > = 2, i.e. I and j start from 1), there are:

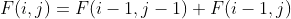
Through observation, it is found that when j=1 or i, the result is 1

Then the recursive formula can be written directly to solve the value of row i and column j:

def foo(i, j):
    if j == 1 or j == i:
        return 1
    return foo(i - 1, j - 1) + foo(i - 1, j)

The operation is as follows (here, the first 6 lines are printed directly for visualization):

for i in range(1, 7):
    res = ''
    for j in range(1, i + 1):
        res += str(foo(i, j)) + ' '
    print(res.center(20, '-'))

'''
---------1 ---------
--------1 1 --------
-------1 2 1 -------
------1 3 3 1 ------
-----1 4 6 4 1 -----
---1 5 10 10 5 1 ---
'''

Summary:

So far, there are some simple cases of single recursion. Note that:

• We need a return to return

1. Terminate recursion; 2. Get the most basic return value

• We need to construct a recurrence formula

It is responsible for the things we want to calculate from large to small, from more to less, from macro to micro, and then subdivide to our minimum element / termination condition. After obtaining the return value, we start from small to large, from less to more, from micro to macro, and add (subtract, multiply and divide) to the final desired result.

2, Double recursion

Note: the names of basic recursion and double recursion are all my own. Don't take them seriously.

Review: let's write a recursion first. It doesn't make much sense. Can you see what it finally outputs?

def foo(n):
    if n > 0:
        print(n)
    return foo(n - 1)

print(foo(3))

In fact, this code will report an error after outputting 3 2 1, because we lack the termination condition and print is not return. Termination conditions should be used together with return to ensure that recursion can be terminated.

Here we modify it,

def foo(n):
    if n > 0:
        print(n)
        return foo(n - 1)


print(foo(3))

'''
3
2
1
None
'''

Double recursion:

Note: the difficulty may be increased here. Please think carefully.

First look at the code, think about the differences between the three situations, think about the results, and then look at the answer.

Case 1, 2 and 3:

def foo(n):
    if n > 0:
        print(n)
        foo(n - 1)
        foo(n - 1)

def foo(n):
    if n > 0:
        foo(n - 1)
        print(n)
        foo(n - 1)

def foo(n):
    if n > 0:
        foo(n - 1)
        foo(n - 1)
        print(n)

First of all, we don't calculate addition, subtraction, multiplication and division here, so we don't have anything like return. For convenience, we only study what happens inside the function when double recursion.

If you just take it in when n=2 and simply calculate it, you might as well guess the law through this attempt. In order to make yourself easy to accept, even if it can't be called the law, we should also call it the law as what we found.

Someone may be in a hurry. Don't worry.

For case 1:

(ignore None, the same below)

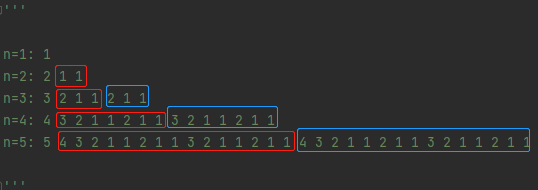
We can see that before double recursion, the largest number is ahead. Because our recursion terminates at 1, there is 211. The number greater than 2 is 3, and we have 3211 + 211 - > 3211211; If the number larger than 3 is 4, we have 43211211 + 3211211 - > 432112113211211

For case 2:

We can see that the maximum number between double recursions is in the middle. Because our recursion terminates at 1, there is 121. The number larger than 2 is 3. We have 121, 3, 121, 4, 1213121, 4, 1213121

For case 3:

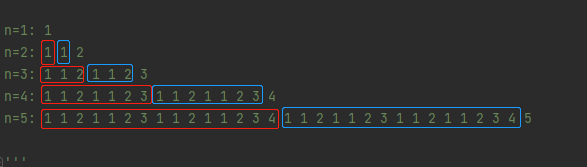
We can see that after double recursion, the maximum number is at the end. Because our recursion terminates at 1, there is 112. The number larger than 2 is 3. We have 112112. When we have 3 and 4, there are 11211231121123 4

At this time, you feel as if you understand and don't understand. No problem.

We have analyzed the microcosmic (i.e. take the numbers one by one and follow the program). We have just analyzed the macroscopic. Please think about whether you understand it.

In fact, we can see that no matter before, during and after printing, the printed results are composed of the results printed last time, that is, finally, the termination condition is the smallest unit. Most conventional recursion will repeat the subproblem many times, whether single recursion or multiple recursion, which is micro. If the last result is taken as a whole, recursion seems to execute only one round or several rounds, which is macro. The macro cannot be separated from the micro, and the micro will automatically form the macro. The difficulty is how to use it flexibly.

microcosmic:

We name the two functions in the function body recursive formula 1 and recursive formula 2, and take one of them as an example:

def foo(n):
    if n > 0:
        foo(n - 1) # Recursive formula 1
        print(n)
        foo(n - 1) # Recursive formula 2

Each time the function enters the function body, first judge whether n is greater than 0. If yes, execute recursive formula 1 downward to the maximum depth (i.e. trigger recursive termination condition). At this time, it is released from the last layer. Recursive formula 1 of the last layer ends the task, executes the print() function of the penultimate layer, prints out the number 1, and then recursive formula 2 of the penultimate layer goes deep into the last layer, It is found that it still does not comply with n > 0. At this time, the recursive formula 1 of the last layer, the penultimate layer and the penultimate layer ends, and the number 2 before 1 is printed Thus, there are 1, 121, 1213121
 

macroscopic:

We always use print() here. In fact, this print can be replaced by some other things, such as assigning a value to a list and printing out the order of numerical changes, We can use it directly according to the specific requirements and combined with the result characteristics of the above three cases.

It may be difficult for beginners to grasp the essence of skilled use. Here are some examples for your reference.

Case 1: the old saying, the tower of Hanoi problem:

Solving the tower of Hanoi problem with python_ suic009 blog - CSDN blog_ Hanoi Tower problem python

Case 2: quick sort

import random
 
#b. e is the range of the list, left and right are the position of the 'pointer' every time it moves to left=right, stop the loop and enter the next round of recursion
def quick_sort(li, b, e):
    if b < e: #Conditions for ending recursion
        left = b
        right = e
        key = li[b]
        while left < right: # You can't write here, which means you have to end with left=right
            while key <= li[right] and left < right: #The equal sign before and will be processed separately if it is added or not (it is recommended to add it and perform one less step of exchange / assignment)
                right -= 1
            if left < right:
                li[left] = li[right]
                left += 1  #Reduce the number of subsequent cycles
 
            while key >= li[left] and left < right:
                left += 1
            if left < right:
                li[right] = li[left]
                right -= 1 #Reduce the number of subsequent cycles
 
        li[left] = key #When the large while is executed, left = right. The middle position is known. It is left.
        quick_sort(li, b, left - 1)
        quick_sort(li, left + 1, e)
 
 
li = [random.randint(1, 9) for i in range(10)]
print(li)
quick_sort(li, 0, len(li) - 1)
print(li)

For other sorting algorithms, see:

Top ten sorting algorithms_ suic009 blog - CSDN blog 

Case 3: first, middle and last order traversal of binary tree (just look at recursive traversal):

class BST:
    # slightly
 
    # Preorder traversal
    def pre_order(self, root):
        if root:
            print(root.data, end=' ')
            self.pre_order(root.lchild)
            self.pre_order(root.rchild)
 
    # Middle order traversal
    def in_order(self, root):
        if root:
            self.in_order(root.lchild)
            print(root.data, end=' ')
            self.in_order(root.rchild)
 
 
    # Postorder traversal
    def post_order(self, root):
        if root:
            self.post_order(root.lchild)
            self.post_order(root.rchild)
            print(root.data, end=' ')
 
    # slightly

For details of binary tree code, see the link below. Click the binary tree in the article directory.

Beginner data structure (biased towards python users)_ suic009 blog - CSDN blog