Concept of red black tree
Red black tree is a binary search tree, but a storage bit is added on each node to represent the color of the node. This color can be red or black, so we call it red black tree.
By limiting the coloring mode of each node on any path from root to leaf, the red black tree ensures that no path will be twice as long as other paths, so the red black tree is approximately balanced.
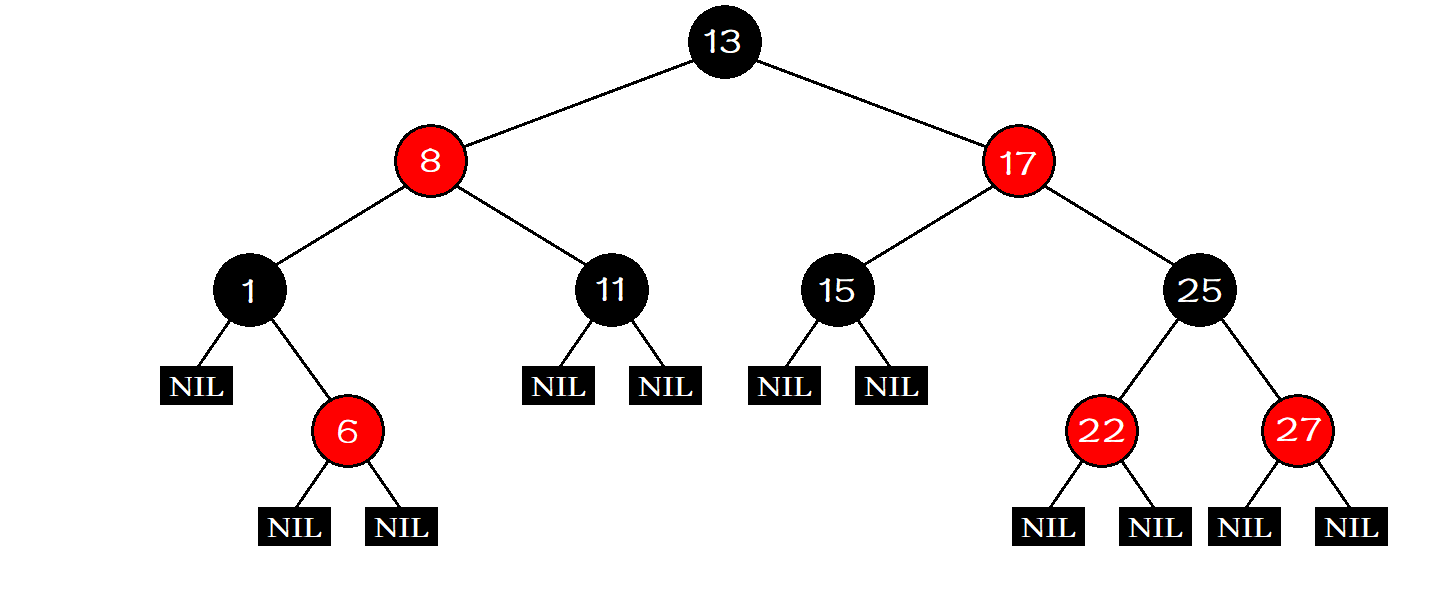
Properties of red black tree
Red black tree has the following five properties:
- Each node is either red or black.
- The root node is black.
- If a node is red, its two child nodes are black.
- For each node, the simple path from the node to all its descendant leaf nodes contains the same number of black nodes.
- Each leaf node is black (the leaf node specified here is an empty node).
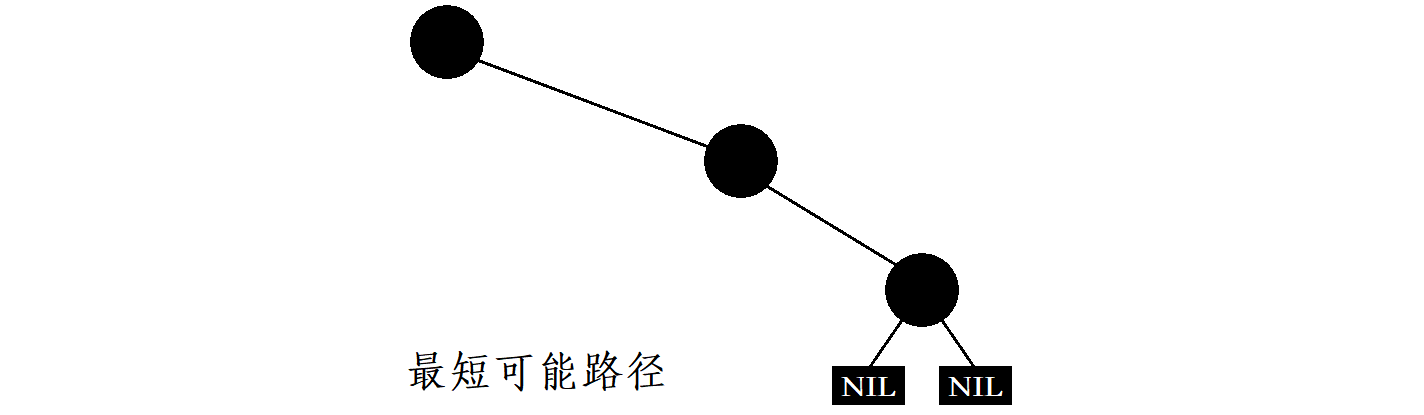
How can red black trees ensure that the longest possible path from root to leaf does not exceed twice the shortest possible path?
According to property 3 of the red black tree, it can be concluded that there will be no continuous red nodes in the red black tree, and according to property 4, the number of black nodes in all paths from a node to its descendant leaf nodes is the same.
We assume that in a red black tree, the number of black nodes in all paths from root to leaf is zero
N
N
N, then the shortest path is the path composed of all black nodes, that is, the length is
N
N
N.
The longest possible path is a path composed of a black node and a red node. The number of black nodes and red nodes in the path is the same, that is, the length is
2
N
2N
2N.
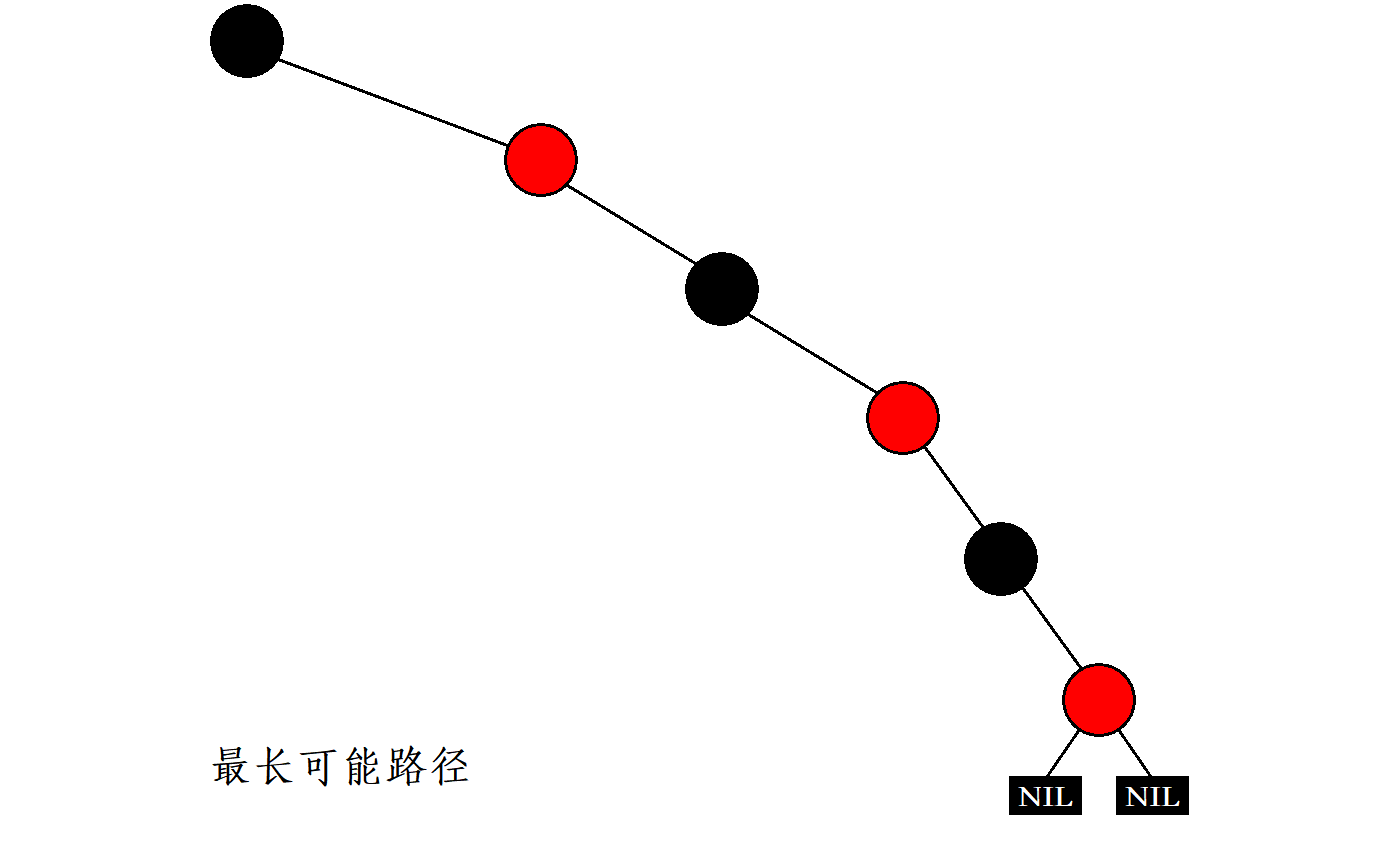
Therefore, the longest possible path from root to leaf of red black tree will not exceed twice the shortest possible path.
Definition of red black tree node
Here we directly implement the red black tree of KV model. In order to facilitate the rotation operation of subsequent order, the node of red black tree is defined as trigeminal chain structure. In addition, a new member variable is added to represent the color of the node.
template<class K, class V>
struct RBTreeNode
{
//Trigeminal chain
RBTreeNode<K, V>* _left;
RBTreeNode<K, V>* _right;
RBTreeNode<K, V>* _parent;
//Stored key value pairs
pair<K, V> _kv;
//Node color
int _col; //Red / Black
//Constructor
RBTreeNode(const pair<K, V>& kv)
:_left(nullptr)
, _right(nullptr)
, _parent(nullptr)
, _kv(kv)
, _col(RED)
{}
};
Here, we can use enumeration to define the color of nodes, which can increase the readability and maintainability of the code and facilitate subsequent debugging operations.
//Enumeration defines the color of the node
enum Colour
{
RED,
BLACK
};
Why is the node color set to red by default when constructing nodes?
When we insert nodes into the red black tree, if we insert black nodes, the number of black nodes on the insertion path is one more than that on other paths, that is, the property 4 of the red black tree is destroyed. At this time, we need to adjust the red black tree.
If the node we insert into the red black tree is red, and its parent node is also red, it indicates that there are continuous red nodes, that is, it destroys the property 3 of the red black tree. At this time, we need to adjust the red black tree; However, if the parent node is black, we do not need to adjust the red black tree, and the requirements of the red black tree are still met after insertion.
To sum up:
- Inserting a black node will certainly destroy the nature 4 of the red black tree, and the red black tree must be adjusted.
- Inserting a red node may destroy the nature 3 of the red black tree and adjust the red black tree.
After weighing the pros and cons, when we construct a node for insertion, the color of the node is set to red by default.
Insertion of red black tree
The logic of red black tree insertion node is divided into three steps:
- According to the insertion method of binary search tree, find the position to be inserted.
- Insert the node to be inserted into the tree.
- If the parent node of the inserted node is red, the red black tree needs to be adjusted.
The logic of the first two steps is the same as that of the binary search tree when inserting nodes. The key of the red black tree is the adjustment of the red black tree in the third step.
How is the red black tree adjusted after inserting nodes?
In fact, the red black tree is not necessarily adjusted after inserting the node. If the parent node of the inserted node is black, we don't need to adjust the red black tree, because this node insertion does not destroy the five properties of the red black tree.
The red black tree needs to be adjusted only when the parent node of the inserted node is red, because the inserted node is red by default. If the parent node of the inserted node is also red, then continuous red nodes appear. Therefore, the red black tree needs to be adjusted.
Because the parent node of the inserted node is red, it means that the parent node is not the root node (the root node is black), so the grandfather node of the inserted node (the parent node of the parent node) must exist.
How to adjust the red black tree depends mainly on the uncle of the inserted node (the brother node of the parent node of the inserted node). According to the different uncles of the inserted node, the adjustment of the red black tree can be divided into three cases.
Case 1: the uncle of the inserted node exists, and the color of the uncle is red.
At this time, in order to avoid continuous red nodes, we can turn the parent node black, but in order to keep the number of black nodes in each path unchanged, we also need to turn the grandfather node red and then turn the uncle black. In this way, the number of black nodes in each path is kept unchanged, and the problem of continuous red nodes is solved.
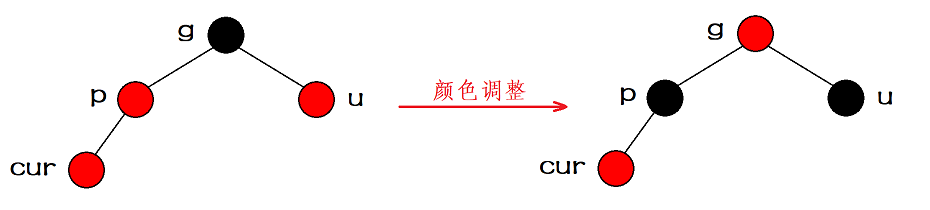
However, the adjustment is not over yet, because at this time, the grandfather node turns red. If the grandfather node is the root node, we can directly turn the grandfather node into black. At this time, the number of black nodes in each path is increased by one.
However, if the grandfather node is not the root node, we need to treat the grandfather node as a newly inserted node, and then judge whether its parent node is red. If its parent node is also red, we need to adjust it according to different uncles.
Therefore, the abstract diagram of case 1 is shown as follows:
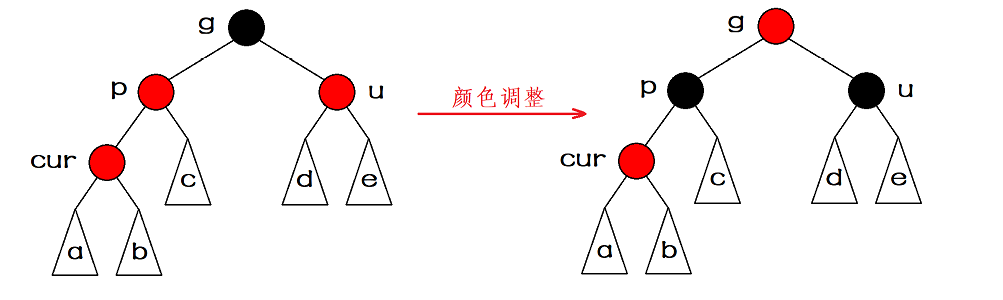
Note: when the uncle exists and is red, the adjustment method is the same whether the cur node is the left child or the right child of the parent.
Case 2: the uncle of the inserted node exists, and the color of the uncle is black.
This situation must occur during the continuous upward adjustment in case 1, that is, the cur node in this case must not be the newly inserted node, but the grandfather node in the last adjustment in case 1, as shown in the following figure:
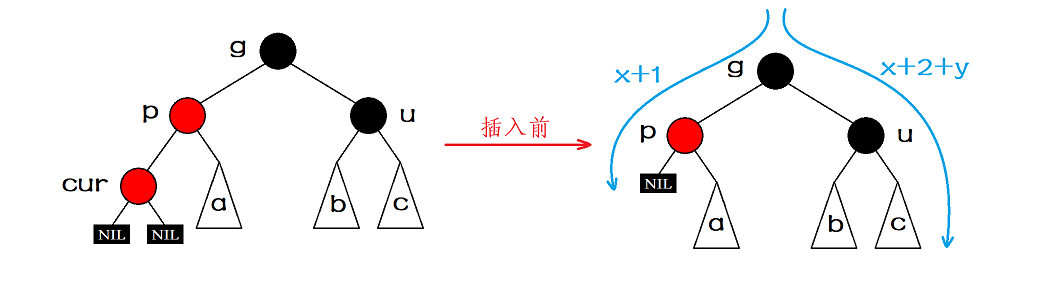
We set the number of black nodes above the grandfather node in the path to
x
x
x. Set the number of black nodes under the uncle node to
y
y
y. Before inserting the node, the number of black nodes in the two paths shown in the figure is
x
+
1
x+1
x+1 and
x
+
2
+
y
x+2+y
x+2+y, obviously
x
+
2
+
y
x+2+y
x+2+y must be greater than
x
+
1
x+1
x+1, so it does not meet the requirements of the red black tree before inserting the node. Therefore, it must be a case that the uncle node exists and is black, which will only occur in the process of upward adjustment.
Note:
- It is a path from the root node to the empty position, rather than a path from the root node to the leaf node where the left and right nodes are empty.
- Both cases 2 and 3 need to be rotated. There is no need to continue to adjust upward after the rotation. Therefore, case 2 must occur in the process of upward adjustment from case 1.
When the uncle exists and is black, it is impossible to deal with the discoloration simply. At this time, we need to rotate it. If the relationship between grandparents and grandchildren is a straight line (cur, parent and grandfather are a straight line), we need to perform a single rotation operation first, and then adjust the color. After the color adjustment, the root node of the rotated subtree is black, so there is no need to continue to process upward.
The abstract diagram is shown as follows:
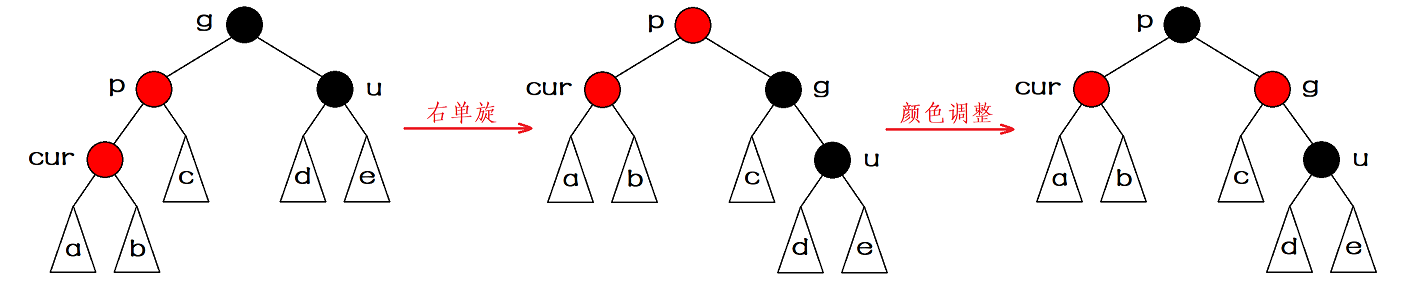
Note: when the linear relationship is, parent is the right child of grandfather and cur is the right child of parent, the left single rotation operation needs to be carried out first, and then the color adjustment.
If the relationship between grandparents and grandchildren is discounted (cur, parent and grandfather are discounted), we need to double rotate first, and then adjust the color. After the color adjustment, the root of the rotated subtree is black, so there is no need to continue to process upward.
The abstract diagram is shown as follows:
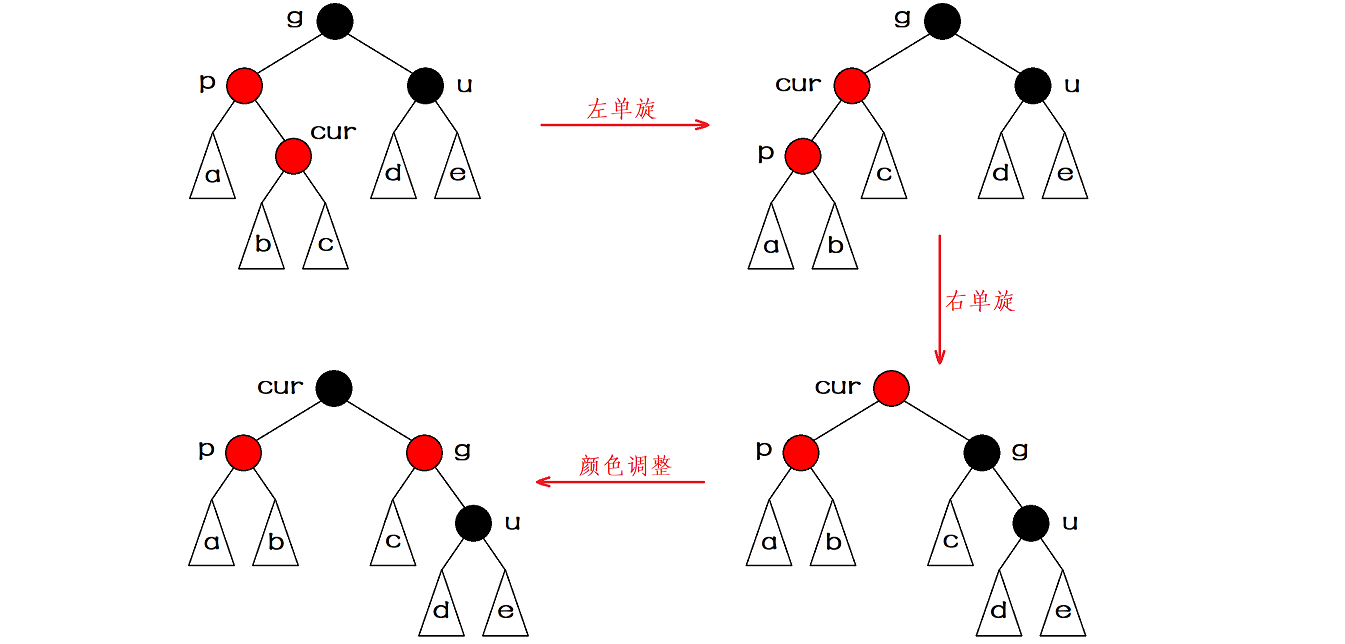
Note: when the discount relationship is, parent is the right child of grandfather and cur is the left child of parent, you need to perform right and left double rotation operation first, and then adjust the color.
Case 3: the uncle of the inserted node does not exist.
In this case, the cur node must be a newly inserted node, but it cannot come from the change of the situation. Because the uncle does not exist, it means that it is impossible to hang a black node under the parent, as shown in the following figure:

If black nodes are hung under the parent before insertion, the number of black nodes in the two paths in the figure will be different, and the parent is red. Therefore, red nodes cannot be hung under the parent, so the cur node in this case must be a newly inserted node.
As in case 2, if the relationship between grandparents and grandchildren is a straight line (cur, parent and grandfather are a straight line), we need to perform a single rotation operation first, and then adjust the color. After the color adjustment, the root node of the rotated subtree is black, so there is no need to continue to process upward.
The abstract diagram is shown as follows:
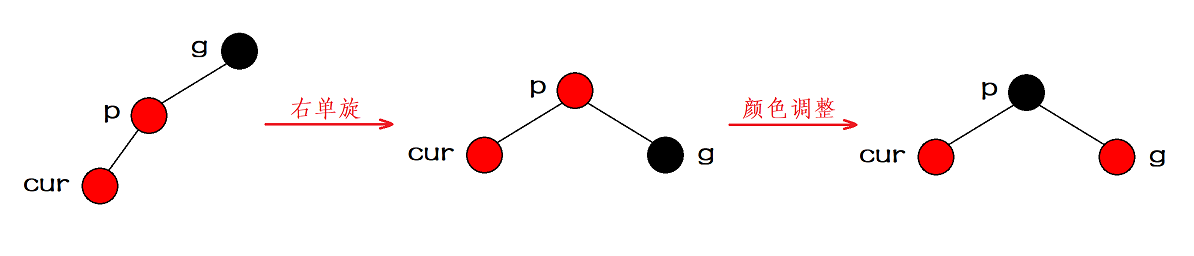
Note: when the linear relationship is, parent is the right child of grandfather and cur is the right child of parent, the left single rotation operation needs to be carried out first, and then the color adjustment.
If the relationship between grandparents and grandchildren is discounted (cur, parent and grandfather are discounted), we need to double rotate first, and then adjust the color. After the color adjustment, the root of the rotated subtree is black, so there is no need to continue to process upward.
The abstract diagram is shown as follows:
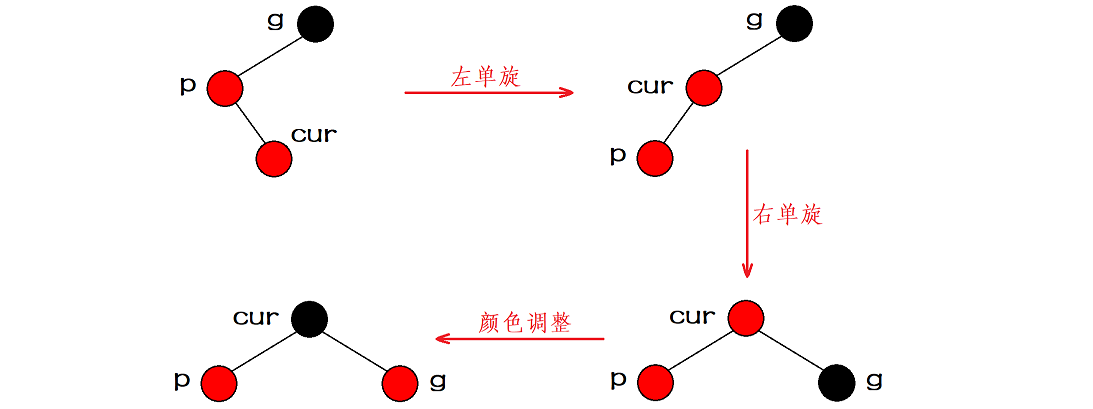
Note: when the discount relationship is, parent is the right child of grandfather and cur is the left child of parent, you need to perform right and left double rotation operation first, and then adjust the color.
The code is as follows:
//Insert function
pair<Node*, bool> Insert(const pair<K, V>& kv)
{
if (_root == nullptr) //If the red black tree is empty, the inserted node is directly used as the root node
{
_root = new Node(kv);
_root->_col = BLACK; //The root node must be black
return make_pair(_root, true); //Insert successful
}
//1. According to the insertion method of binary search tree, find the position to be inserted
Node* cur = _root;
Node* parent = nullptr;
while (cur)
{
if (kv.first < cur->_kv.first) //The key value of the node to be inserted is less than the key value of the current node
{
//Go to the left subtree of the node
parent = cur;
cur = cur->_left;
}
else if (kv.first > cur->_kv.first) //The key value of the node to be inserted is greater than the key value of the current node
{
//Go to the right subtree of the node
parent = cur;
cur = cur->_right;
}
else //The key value of the node to be inserted is equal to the key value of the current node
{
return make_pair(cur, false); //Insert failed
}
}
//2. Insert the node to be inserted into the tree
cur = new Node(kv); //Construct a node according to the given value
Node* newnode = cur; //Record the newly inserted node (convenient for subsequent return)
if (kv.first < parent->_kv.first) //The key value of the new node is less than that of the parent
{
//Insert to the left of the parent
parent->_left = cur;
cur->_parent = parent;
}
else //The key value of the new node is greater than that of the parent
{
//Insert to the right of the parent
parent->_right = cur;
cur->_parent = parent;
}
//3. If the parent node of the inserted node is red, the red black tree needs to be adjusted
while (parent&&parent->_col == RED)
{
Node* grandfather = parent->_parent; //If the parent is red, its parent node must exist
if (parent == grandfather->_left) //parent is grandfather's left child
{
Node* uncle = grandfather->_right; //uncle is grandfather's right child
if (uncle&&uncle->_col == RED) //Case 1: uncle exists and is red
{
//Color adjustment
parent->_col = uncle->_col = BLACK;
grandfather->_col = RED;
//Continue to process upward
cur = grandfather;
parent = cur->_parent;
}
else //Case 2 + case 3: uncle does not exist + uncle exists and is black
{
if (cur == parent->_left)
{
RotateR(grandfather); //Right single rotation
//Color adjustment
grandfather->_col = RED;
parent->_col = BLACK;
}
else //cur == parent->_right
{
RotateLR(grandfather); //Left and right double rotation
//Color adjustment
grandfather->_col = RED;
cur->_col = BLACK;
}
break; //After the subtree is rotated, the root of the subtree becomes black, and there is no need to continue processing upward
}
}
else //parent is grandfather's right child
{
Node* uncle = grandfather->_left; //uncle is grandfather's left child
if (uncle&&uncle->_col == RED) //Case 1: uncle exists and is red
{
//Color adjustment
uncle->_col = parent->_col = BLACK;
grandfather->_col = RED;
//Continue to process upward
cur = grandfather;
parent = cur->_parent;
}
else //Case 2 + case 3: uncle does not exist + uncle exists and is black
{
if (cur == parent->_left)
{
RotateRL(grandfather); //Right left double spin
//Color adjustment
cur->_col = BLACK;
grandfather->_col = RED;
}
else //cur == parent->_right
{
RotateL(grandfather); //Sinistral
//Color adjustment
grandfather->_col = RED;
parent->_col = BLACK;
}
break; //After the subtree is rotated, the root of the subtree becomes black, and there is no need to continue processing upward
}
}
}
_root->_col = BLACK; //The color of the root node is black (it may be changed to red by case 1 and needs to be changed back to black)
return make_pair(newnode, true); //Insert successful
}
//Sinistral
void RotateL(Node* parent)
{
Node* subR = parent->_right;
Node* subRL = subR->_left;
Node* parentParent = parent->_parent;
//Establish the relationship between subRL and parent
parent->_right = subRL;
if (subRL)
subRL->_parent = parent;
//Establish the relationship between parent and subR
subR->_left = parent;
parent->_parent = subR;
//Establish the relationship between subR and parentParent
if (parentParent == nullptr)
{
_root = subR;
_root->_parent = nullptr;
}
else
{
if (parent == parentParent->_left)
{
parentParent->_left = subR;
}
else
{
parentParent->_right = subR;
}
subR->_parent = parentParent;
}
}
//Right single rotation
void RotateR(Node* parent)
{
Node* subL = parent->_left;
Node* subLR = subL->_right;
Node* parentParent = parent->_parent;
//Establish the relationship between subLR and parent
parent->_left = subLR;
if (subLR)
subLR->_parent = parent;
//Establish the relationship between parent and subL
subL->_right = parent;
parent->_parent = subL;
//Establish the relationship between subL and parentParent
if (parentParent == nullptr)
{
_root = subL;
_root->_parent = nullptr;
}
else
{
if (parent == parentParent->_left)
{
parentParent->_left = subL;
}
else
{
parentParent->_right = subL;
}
subL->_parent = parentParent;
}
}
//Left and right double rotation
void RotateLR(Node* parent)
{
RotateL(parent->_left);
RotateR(parent);
}
//Right left double spin
void RotateRL(Node* parent)
{
RotateR(parent->_right);
RotateL(parent);
}
Note: after the red black tree is adjusted, the color of the root node needs to be changed to black, because the root node of the red black tree may be changed to red during the adjustment of case 1.
Verification of red black tree
Red black tree is also a special binary search tree, so we can first obtain the middle order traversal sequence of binary tree to judge whether the binary tree meets the properties of binary search tree.
The code is as follows:
//Medium order traversal
void Inorder()
{
_Inorder(_root);
}
//Middle order ergodic subfunction
void _Inorder(Node* root)
{
if (root == nullptr)
return;
_Inorder(root->_left);
cout << root->_kv.first << " ";
_Inorder(root->_right);
}
However, medium order order can only prove that it is a binary search tree. To prove that the binary tree is a red black tree, we need to verify whether the binary tree meets the properties of red black tree.
The code is as follows:
//Judge whether it is a red black tree
bool ISRBTree()
{
if (_root == nullptr) //An empty tree is a red black tree
{
return true;
}
if (_root->_col == RED)
{
cout << "error: The root node is red" << endl;
return false;
}
//Find the leftmost path as the reference value of the number of black nodes
Node* cur = _root;
int BlackCount = 0;
while (cur)
{
if (cur->_col == BLACK)
BlackCount++;
cur = cur->_left;
}
int count = 0;
return _ISRBTree(_root, count, BlackCount);
}
//Determine whether it is a subfunction of red black tree
bool _ISRBTree(Node* root, int count, int BlackCount)
{
if (root == nullptr) //The path has been completed
{
if (count != BlackCount)
{
cout << "error: The number of black nodes is not equal" << endl;
return false;
}
return true;
}
if (root->_col == RED&&root->_parent->_col == RED)
{
cout << "error: There are continuous red nodes" << endl;
return false;
}
if (root->_col == BLACK)
{
count++;
}
return _ISRBTree(root->_left, count, BlackCount) && _ISRBTree(root->_right, count, BlackCount);
}
Search of red black tree
As like as two peas search tree, the search function of red black tree is exactly the same as the two fork search tree.
- If the tree is empty, the search fails and nullptr is returned.
- If the key value is less than the value of the current node, it should be searched in the left subtree of the node.
- If the key value is greater than the value of the current node, it should be searched in the right subtree of the node.
- If the key value is equal to the value of the current node, the search is successful and the corresponding node is returned.
The code is as follows:
//Find function
Node* Find(const K& key)
{
Node* cur = _root;
while (cur)
{
if (key < cur->_kv.first) //The key value is less than the value of this node
{
cur = cur->_left; //Search in the left subtree of the node
}
else if (key > cur->_kv.first) //The key value is greater than the value of this node
{
cur = cur->_right; //Find in the right subtree of the node
}
else //The target node was found
{
return cur; //Return to this node
}
}
return nullptr; //Search failed
}
Red black tree deletion
Red black tree deletion is more difficult to understand than insertion, but it's ok as long as you're careful.
Step 1: find the actual node to be deleted
The process of finding the node is the same as that of finding the node to be deleted by binary search tree. If the left and right subtrees of the node to be deleted are not empty, the replacement method needs to be used for deletion. Therefore, what we finally need to delete is that there is at least one empty node in the left and right subtrees.
After finding the actual node to be deleted, do not delete the node first, otherwise it is not easy to control when adjusting the red black tree. After finding the actual node to be deleted, adjust the red black tree immediately.
Step 2: adjust the red black tree
Before adjusting the red black tree, we first judge whether the deletion of this node will destroy the nature of the red black tree. If so, we need to adjust the red black tree.
If the actual deleted node is a red node, the deletion operation will not destroy the nature of the red black tree, so we do not need to adjust the red black tree. On the contrary, if the deleted node is a black node, we need to adjust the red black tree, because the deletion of black nodes will reduce the number of black nodes in some paths, which will destroy the property 4 of the red black tree.
Let's start with the simplest case, that is, the case where only one child of the node to be deleted is empty.
In this case, the node to be deleted either has a left child or a right child, but whether it is a left child or a right child, the child must be red, because if the child is black, the number of black nodes in the long blue path shown in the figure is more than that in the short blue path, which is not in line with the nature of the red black tree.
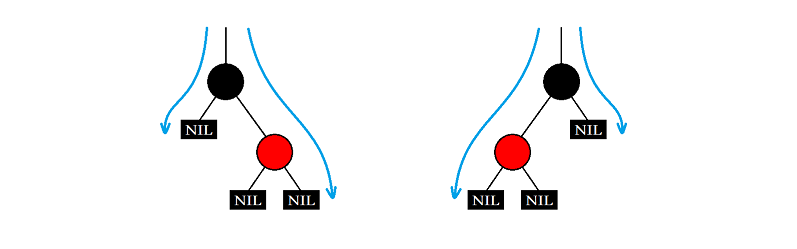
In addition, continuous red nodes are not allowed in the red black tree, so in this case, there are only two actual situations as shown in the figure. At this time, we can directly turn the red child of the node to be deleted into black, because when the node is actually deleted later, this child will be connected to the parent node of the deleted node, After connection, we delete a red node, and the red black tree is adjusted.
Let's talk about the more complex situation, that is, the left and right children of the node to be deleted are empty.
We take the left child of the node to be deleted as an example, which can be divided into the following four cases:
Illustration:
- If the parent node is white, it indicates that the parent node may be red or black.
- If the bL or bR node is white, it indicates that it may be a red node or a black node, or even the node does not exist.
- When bL and bR nodes are black, it indicates that they may be black nodes or the node does not exist.
Case 1: brother is red.

When the brother of the node to be deleted is red, we first make a left single rotation with the parent as the rotation point, and then change the color of the brother to black and the color of the parent to red. At this time, we analyze the cur of the node to be deleted, and case 1 is converted to case 2, 3 or 4.
Case 2: the brother is black, and the left and right children are black or empty.
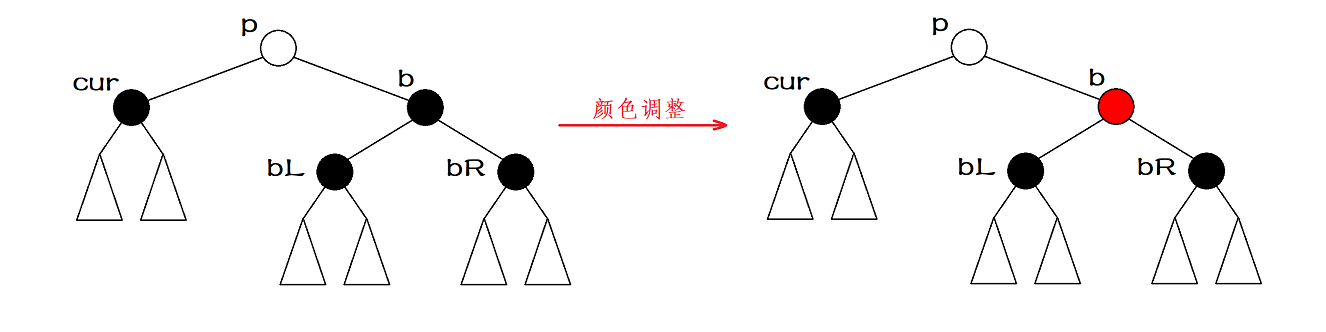
In this case, we directly change the color of the brother to red. At this time, we decide whether to end the adjustment of the red black tree according to the color of the parent. If the color of the parent is red, we can end the adjustment of the red black tree after changing the parent to black; If the color of the parent is black, we need to analyze the parent node as the cur node in the next adjustment, and case 2 may be any of cases 1, 2, 3 and 4 in the next adjustment.
Case 3: the brother is black, and the left child is a red node, and the right child is a black node or empty.
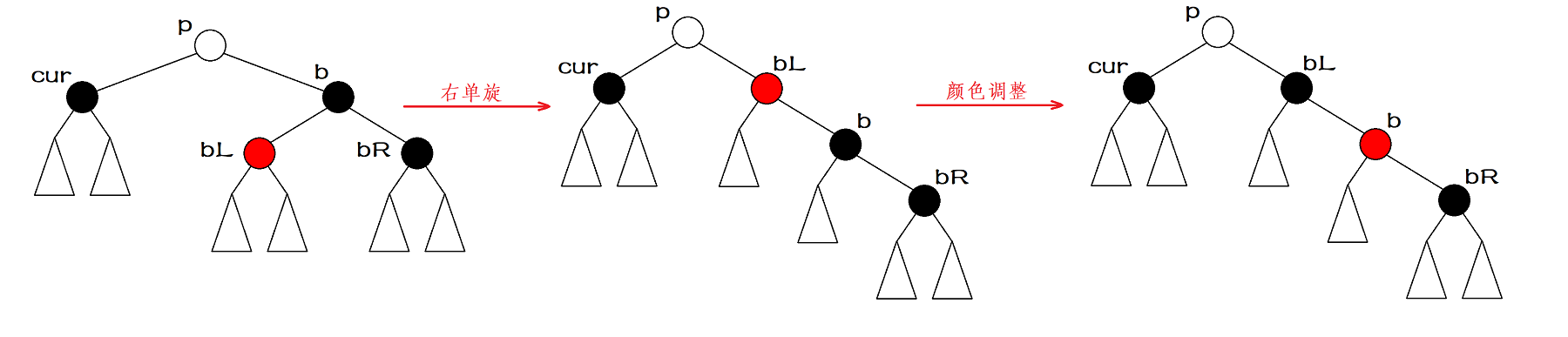
In this case, we first make a right single rotation with brother as the rotation point, then change the brother node to red and the brother left to black. At this time, we will analyze the situation of deleting the node cur, and case 3 will be converted to case 4.
Case 4: the brother is black and the right child is red.

After the treatment of situation 4, the adjustment of red black tree must be over. In case 4, we first make a left single rotation with the parent as the rotation point, then assign the color of the parent to the brother, then change the color of the parent to black, and finally change the brother right to black. At this time, the adjustment of the red black tree is over.
Explain:
- The four cases when the node to be deleted is the right child of its parent node are similar to the above four cases, which are not listed here.
- If the node to be deleted has no parent node, that is, when the node to be deleted is the root node, it will be deleted when the node is found. It doesn't need to be considered here. See the code for details.
Here, it is necessary to explain the switching of various situations. You may be worried that when adjusting the red black tree, you can always switch back and forth without jumping out. Let's analyze this below:
First of all, after entering situation 4, the adjustment of red and black trees must be over. Secondly, after entering situation 3, it will enter situation 4 next time, and the adjustment of red black tree will end. So there is no problem with situation three and situation four. You can only struggle with situation one and situation two.
Case 1 will be switched to case 2, 3 and 4. Therefore, as long as case 2 can have a way to exit, all cases can exit.
In case 2, we said that if the color of the parent is red, we can end the adjustment of the red black tree after changing the parent to black. Will the color of the parent be not red but black every time we enter case 2?
Of course, it is possible, but if we keep adjusting upward, we will always adjust to the root node of the red black tree. When we adjust to the root node, we do not need to adjust. At this time, although the root node is black, it does not affect it, which only means that the number of black nodes contained in each path from root to leaf has increased by one, At this time, the nature of the red black tree is not destroyed, and the adjustment of the red black tree is completed. Therefore, the problem of switching back and forth in these four situations without jumping out will not occur in the adjustment process.
Step 3: delete the node
After the red black tree is adjusted, we can delete the node. The way to delete the node is very simple. If the node to be deleted has left or right children, we can connect its left or right children to the lower part of the parent node of the node to be deleted, and then delete the node to be deleted.
The code is as follows:
//Delete function
bool Erase(const K& key)
{
//Used to traverse a binary tree
Node* parent = nullptr;
Node* cur = _root;
//Used to mark the actual node to be deleted and its parent node
Node* delParentPos = nullptr;
Node* delPos = nullptr;
while (cur)
{
if (key < cur->_kv.first) //The given key value is less than the key value of the current node
{
//Go to the left subtree of the node
parent = cur;
cur = cur->_left;
}
else if (key > cur->_kv.first) //The given key value is greater than the key value of the current node
{
//Go to the right subtree of the node
parent = cur;
cur = cur->_right;
}
else //The node to be deleted was found
{
if (cur->_left == nullptr) //The left subtree of the node to be deleted is empty
{
if (cur == _root) //The node to be deleted is the root node
{
_root = _root->_right; //Let the right subtree of the root node be the new root node
if (_root)
{
_root->_parent = nullptr;
_root->_col = BLACK; //The root node is black
}
delete cur; //Delete original root node
return true;
}
else
{
delParentPos = parent; //Mark the parent node of the actual deleted node
delPos = cur; //Mark the node actually deleted
}
break; //Adjust the red black tree and actually delete the nodes
}
else if (cur->_right == nullptr) //The right subtree of the node to be deleted is empty
{
if (cur == _root) //The node to be deleted is the root node
{
_root = _root->_left; //Let the left subtree of the root node be the new root node
if (_root)
{
_root->_parent = nullptr;
_root->_col = BLACK; //The root node is black
}
delete cur; //Delete original root node
return true;
}
else
{
delParentPos = parent; //Mark the parent node of the actual deleted node
delPos = cur; //Mark the node actually deleted
}
break; //Adjust the red black tree and actually delete the nodes
}
else //The left and right subtrees of the node to be deleted are not empty
{
//Substitution deletion
//Find the node with the smallest key value in the right subtree of the node to be deleted as the actual deleted node
Node* minParent = cur;
Node* minRight = cur->_right;
while (minRight->_left)
{
minParent = minRight;
minRight = minRight->_left;
}
cur->_kv.first = minRight->_kv.first; //Change the key of the node to be deleted to the key of minRight
cur->_kv.second = minRight->_kv.second; //Change the value of the node to be deleted to the value of minRight
delParentPos = minParent; //Mark the parent node of the actual deleted node
delPos = minRight; //Mark the node actually deleted
break; //Adjust the red black tree and actually delete the nodes
}
}
}
if (delPos == nullptr) //delPos has not been modified, which means that the node to be deleted is not found
{
return false;
}
//Record the node to be deleted and its parent node (for subsequent actual deletion)
Node* del = delPos;
Node* delP = delParentPos;
//Adjust red black tree
if (delPos->_col == BLACK) //Black nodes are deleted
{
if (delPos->_left) //The node to be deleted has a red left child (it can't be black)
{
delPos->_left->_col = BLACK; //Turn the red left child black
}
else if (delPos->_right) //The node to be deleted has a red right child (cannot be black)
{
delPos->_right->_col = BLACK; //Turn the red right child black
}
else //The left and right of the node to be deleted are empty
{
while (delPos != _root) //It may be adjusted all the way to the root node
{
if (delPos == delParentPos->_left) //The node to be deleted is the left child of its parent node
{
Node* brother = delParentPos->_right; //A sibling node is the right child of its parent node
//Case 1: brother is red
if (brother->_col == RED)
{
delParentPos->_col = RED;
brother->_col = BLACK;
RotateL(delParentPos);
//Need to continue processing
brother = delParentPos->_right; //Update brother (otherwise code that executes other situations in this loop will make an error)
}
//Case 2: the brother is black, and the left and right children are black or empty
if (((brother->_left == nullptr) || (brother->_left->_col == BLACK))
&& ((brother->_right == nullptr) || (brother->_right->_col == BLACK)))
{
brother->_col = RED;
if (delParentPos->_col == RED)
{
delParentPos->_col = BLACK;
break;
}
//Need to continue processing
delPos = delParentPos;
delParentPos = delPos->_parent;
}
else
{
//Case 3: the brother is black, and the left child is a red node, and the right child is a black node or empty
if ((brother->_right == nullptr) || (brother->_right->_col == BLACK))
{
brother->_left->_col = BLACK;
brother->_col = RED;
RotateR(brother);
//Need to continue processing
brother = delParentPos->_right; //Update brother (otherwise an error will occur when executing the code in case 4 below)
}
//Case 4: the brother is black and the right child is red
brother->_col = delParentPos->_col;
delParentPos->_col = BLACK;
brother->_right->_col = BLACK;
RotateL(delParentPos);
break; //Situation four the adjustment will be finished after execution.
}
}
else //delPos == delParentPos->_ Right / / the node to be deleted is the left child of its parent node
{
Node* brother = delParentPos->_left; //A sibling node is the left child of its parent node
//Case 1: brother is red
if (brother->_col == RED) //brother is red
{
delParentPos->_col = RED;
brother->_col = BLACK;
RotateR(delParentPos);
//Need to continue processing
brother = delParentPos->_left; //Update brother (otherwise code that executes other situations in this loop will make an error)
}
//Case 2: the brother is black, and the left and right children are black or empty
if (((brother->_left == nullptr) || (brother->_left->_col == BLACK))
&& ((brother->_right == nullptr) || (brother->_right->_col == BLACK)))
{
brother->_col = RED;
if (delParentPos->_col == RED)
{
delParentPos->_col = BLACK;
break;
}
//Need to continue processing
delPos = delParentPos;
delParentPos = delPos->_parent;
}
else
{
//Case 3: the brother is black, and the right child is a red node, and the left child is a black node or empty
if ((brother->_left == nullptr) || (brother->_left->_col == BLACK))
{
brother->_right->_col = BLACK;
brother->_col = RED;
RotateL(brother);
//Need to continue processing
brother = delParentPos->_left; //Update brother (otherwise an error will occur when executing the code in case 4 below)
}
//Case 4: the brother is black and the left child is red
brother->_col = delParentPos->_col;
delParentPos->_col = BLACK;
brother->_left->_col = BLACK;
RotateR(delParentPos);
break; //Situation four the adjustment will be finished after execution.
}
}
}
}
}
//Actual deletion
if (del->_left == nullptr) //The left subtree of the actually deleted node is empty
{
if (del == delP->_left) //The actual deleted node is the left child of its parent node
{
delP->_left = del->_right;
if (del->_right)
del->_right->_parent = delP;
}
else //The actual deleted node is the right child of its parent node
{
delP->_right = del->_right;
if (del->_right)
del->_right->_parent = delP;
}
}
else //The right subtree of the actual deleted node is empty
{
if (del == delP->_left) //The actual deleted node is the left child of its parent node
{
delP->_left = del->_left;
if (del->_left)
del->_left->_parent = delP;
}
else //The actual deleted node is the right child of its parent node
{
delP->_right = del->_left;
if (del->_left)
del->_left->_parent = delP;
}
}
delete del; //Actually delete node
return true;
}
Comparison between red black tree and AVL tree
Both red black tree and AVL tree are efficient balanced binary trees, and the time complexity of adding, deleting, checking and modifying is O ( l o g N ) O(logN) O(logN), but red black trees and AVL trees control binary tree balance differently:
- AVL tree realizes binary tree balance by controlling the height difference between the left and right not to exceed 1, which realizes the strict balance of binary tree.
- By controlling the color of nodes, the red black tree makes the longest possible path in the red black tree not more than twice the shortest possible path, and achieves approximate balance.
Compared with AVL tree, red black tree reduces the number of rotations required when inserting nodes. Therefore, in the structure of frequent addition and deletion, neutral energy is better than AVL tree. In practical application, red black tree is mostly used.