1. Marginalization theory
The theories related to marginalization mainly refer to the courses of Gao Bo and he Bo and three references:
- <The Humble Gaussian Distribution>
- <Exactly Sparse Extended Information Filters for Feature-Based SLAM>
- <Consistency Analysis for Sliding-Window Visual Odometry>
1.1 why marginalization?
First of all, we know that if the camera transformation pose is calculated only from the front and rear images, its speed is fast but its accuracy is low, If the global optimization method is adopted (for example, Bundle Adjustment) has high precision but low efficiency. Therefore, the predecessors introduced the sliding window method, which optimizes a fixed number of frames each time, so as to ensure both precision and efficiency. Since it is a sliding window, new image frames will come in and old image frames will leave in the sliding process. The so-called marginalization is to make the image frames leave Open image frames are well utilized.
1.2 how to marginalize?
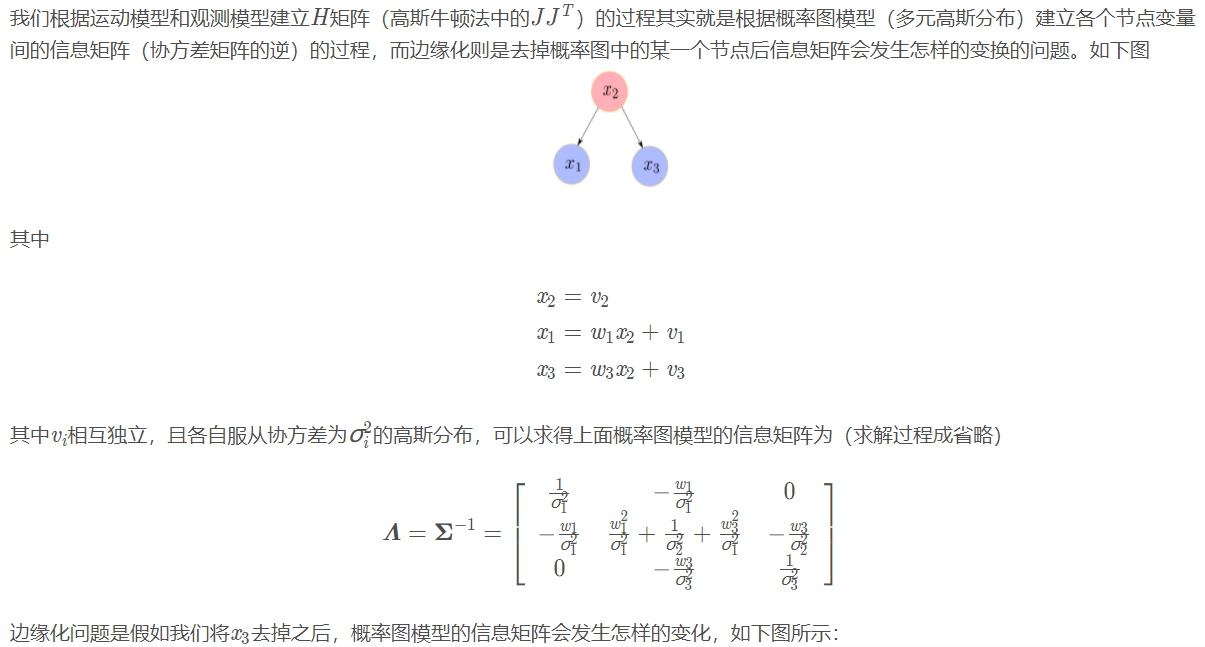

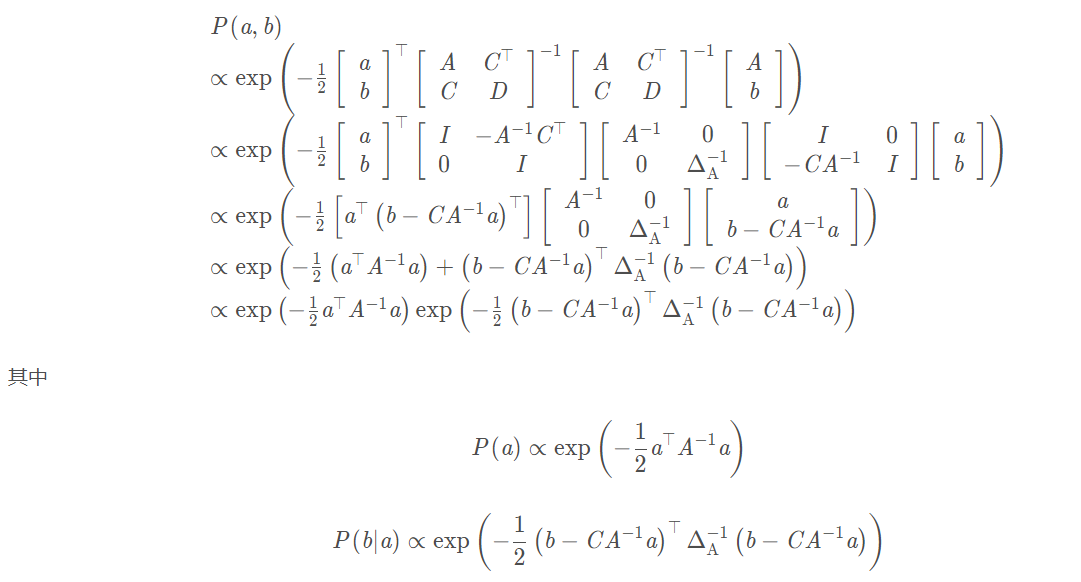


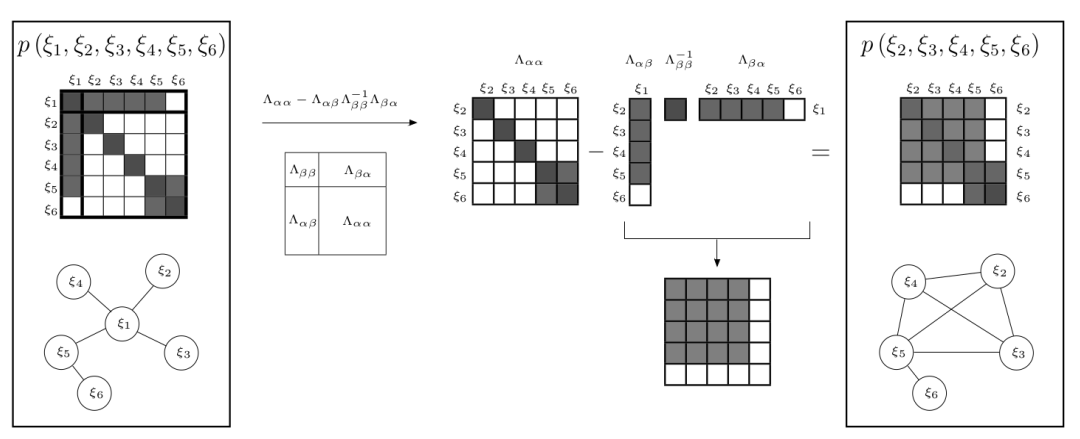

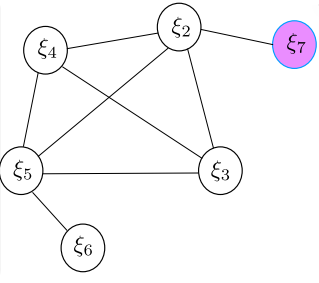
1.3 is there anything to pay attention to in the actual marginalization operation?
A noteworthy problem is the fusion of new and old information, that is, the use of FEJ algorithm, as shown below:
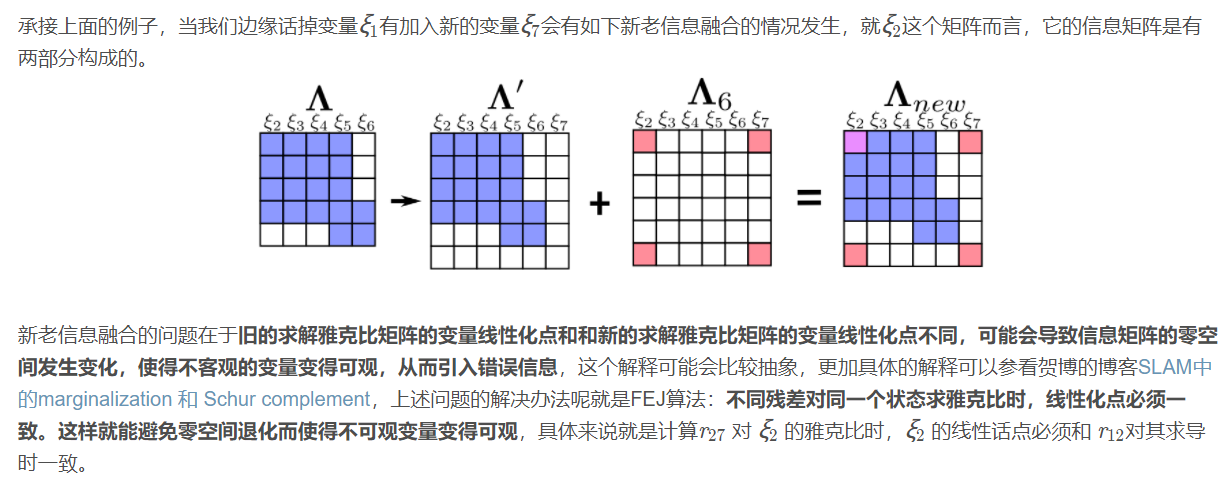
2. Code analysis
It is only the first step to clarify the above theory. Due to the large number of variables optimized by vins mono, the marginalization operation of vins mono is actually much more complex. The marginalization related code of vins mono is in the Estimator In the optimization() function of the Estimator class of CPP, the function will first perform back-end nonlinear optimization, and then the marginalization operation. The marginalization related codes in this function are analyzed below.
2.1 optimization variable analysis
First, we determine which variables are involved in the marginalization operation. This can be seen from the vector2double() function. Because the variables in ceres must use array type, such a function is required for data type conversion, as follows:
void Estimator::vector2double()
{
for (int i = 0; i <= WINDOW_SIZE; i++)
{
para_Pose[i][0] = Ps[i].x();
para_Pose[i][1] = Ps[i].y();
para_Pose[i][2] = Ps[i].z();
Quaterniond q{Rs[i]};
para_Pose[i][3] = q.x();
para_Pose[i][4] = q.y();
para_Pose[i][5] = q.z();
para_Pose[i][6] = q.w();
para_SpeedBias[i][0] = Vs[i].x();
para_SpeedBias[i][1] = Vs[i].y();
para_SpeedBias[i][2] = Vs[i].z();
para_SpeedBias[i][3] = Bas[i].x();
para_SpeedBias[i][4] = Bas[i].y();
para_SpeedBias[i][5] = Bas[i].z();
para_SpeedBias[i][6] = Bgs[i].x();
para_SpeedBias[i][7] = Bgs[i].y();
para_SpeedBias[i][8] = Bgs[i].z();
}
for (int i = 0; i < NUM_OF_CAM; i++)
{
para_Ex_Pose[i][0] = tic[i].x();
para_Ex_Pose[i][1] = tic[i].y();
para_Ex_Pose[i][2] = tic[i].z();
Quaterniond q{ric[i]};
para_Ex_Pose[i][3] = q.x();
para_Ex_Pose[i][4] = q.y();
para_Ex_Pose[i][5] = q.z();
para_Ex_Pose[i][6] = q.w();
}
VectorXd dep = f_manager.getDepthVector();
for (int i = 0; i < f_manager.getFeatureCount(); i++)
para_Feature[i][0] = dep(i);
if (ESTIMATE_TD)
para_Td[0][0] = td;
}
It can be seen that the optimization variables generated here are:
- para_Pose (6-D, camera pose)
- para_SpeedBias (9-d, camera speed, acceleration offset, angular velocity offset)
- para_Ex_Pose (6-D, camera IMU external reference)
- para_Feature (1D, feature point depth)
- para_Td (1D, calibration synchronization time)
It consists of five parts. These optimization variables are treated as a whole in the later marginalization operation.
2.1 MarginalizationInfo class analysis
Then, let's take a look at the and marginalization class MarginalizationInfo
class MarginalizationInfo
{
public:
~MarginalizationInfo();
int localSize(int size) const;
int globalSize(int size) const;
//Add stagger block related information (optimization variable, variable to be marg)
void addResidualBlockInfo(ResidualBlockInfo *residual_block_info);
//Calculate the Jacobian corresponding to each residual and update the parameter_block_data
void preMarginalize();
//pos refers to all variable dimensions, m refers to the variable to be marg inated, and N refers to the variable to be reserved
void marginalize();
std::vector<double *> getParameterBlocks(std::unordered_map<long, double *> &addr_shift);
std::vector<ResidualBlockInfo *> factors;//All observations
int m, n;//m is the number of variables to be marginalized and n is the number of variables to be retained
std::unordered_map<long, int> parameter_block_size; //< optimize variable memory address, localsize >
int sum_block_size;
std::unordered_map<long, int> parameter_block_idx; //< optimize variable memory address, ID in matrix >
std::unordered_map<long, double *> parameter_block_data;//< optimize variable memory address, data >
std::vector<int> keep_block_size; //global size
std::vector<int> keep_block_idx; //local size
std::vector<double *> keep_block_data;
Eigen::MatrixXd linearized_jacobians;
Eigen::VectorXd linearized_residuals;
const double eps = 1e-8;
};
Let's start with variables. There are three unordered variables_ Map related variables are:
- parameter_block_size,
- parameter_block_idx,
- parameter_block_data,
Their key s are the same memory address of long type, while value is the length of each optimization variable, the id of each optimization variable and the data of double pointer type corresponding to each optimization variable.
There are three vector related variables:
- keep_block_size,
- keep_block_idx,
- keep_block_data,
They are the length of each optimization variable retained after marginalization, and the id of each optimization variable is the data of double pointer type corresponding to each optimization variable
also
- linearized_jacobians,
- linearized_residuals,
It refers to the Jacobian matrix and residual vector recovered from the information matrix after marginalization
2.3 step 1: call addResidualBlockInfo()
For functions, it will be more intuitive to directly look at the calls in optimization. First, we will call addResidualBlockInfo() function to add each residual and the optimization variables involved in the residual into the optimization variables described above:
- First, add the previous a priori residual term:
if (last_marginalization_info)
{
vector<int> drop_set;
for (int i = 0; i < static_cast<int>(last_marginalization_parameter_blocks.size()); i++)//last_marginalization_parameter_blocks are the residual blocks left over from the previous round
{
if (last_marginalization_parameter_blocks[i] == para_Pose[0] ||
last_marginalization_parameter_blocks[i] == para_SpeedBias[0])//The optimization variable that needs to be marg dropped, that is, the first variable in the sliding window
drop_set.push_back(i);
}
// construct new marginlization_factor
MarginalizationFactor *marginalization_factor = new MarginalizationFactor(last_marginalization_info);
ResidualBlockInfo *residual_block_info = new ResidualBlockInfo(marginalization_factor, NULL,
last_marginalization_parameter_blocks,
drop_set);
marginalization_info->addResidualBlockInfo(residual_block_info);
}
- Then add the IMU pre integration score between frames 0 and 1 and the related optimization variables between frames 0 and 1
{
if (pre_integrations[1]->sum_dt < 10.0)
{
IMUFactor* imu_factor = new IMUFactor(pre_integrations[1]);
ResidualBlockInfo *residual_block_info = new ResidualBlockInfo(imu_factor, NULL,
vector<double *>{para_Pose[0], para_SpeedBias[0], para_Pose[1], para_SpeedBias[1]},//Optimization variables
vector<int>{0, 1});//Here is 0,1 because 0 and 1 are para_Pose[0], para_SpeedBias[0] is a variable that requires marg
marginalization_info->addResidualBlockInfo(residual_block_info);
}
}
- Finally, add the road marking of frame 0 in the first observation sliding window and the relevant optimization variables of other relevant frames in the sliding window
{
int feature_index = -1;
for (auto &it_per_id : f_manager.feature)
{
it_per_id.used_num = it_per_id.feature_per_frame.size();//Here is to traverse all the feature points of the sliding window
if (!(it_per_id.used_num >= 2 && it_per_id.start_frame < WINDOW_SIZE - 2))
continue;
++feature_index;
int imu_i = it_per_id.start_frame, imu_j = imu_i - 1;//Here is the first observation frame of the feature point
if (imu_i != 0)//If the first observation frame is not the first frame, it will not be considered. Therefore, the sliding window frames with common view relationship with the first frame are used to construct the marg matrix later
continue;
Vector3d pts_i = it_per_id.feature_per_frame[0].point;
for (auto &it_per_frame : it_per_id.feature_per_frame)
{
imu_j++;
if (imu_i == imu_j)
continue;
Vector3d pts_j = it_per_frame.point;
if (ESTIMATE_TD)
{
ProjectionTdFactor *f_td = new ProjectionTdFactor(pts_i, pts_j, it_per_id.feature_per_frame[0].velocity, it_per_frame.velocity,
it_per_id.feature_per_frame[0].cur_td, it_per_frame.cur_td,
it_per_id.feature_per_frame[0].uv.y(), it_per_frame.uv.y());
ResidualBlockInfo *residual_block_info = new ResidualBlockInfo(f_td, loss_function,
vector<double *>{para_Pose[imu_i], para_Pose[imu_j], para_Ex_Pose[0], para_Feature[feature_index], para_Td[0]},//Optimization variables
vector<int>{0, 3});
marginalization_info->addResidualBlockInfo(residual_block_info);
}
else
{
ProjectionFactor *f = new ProjectionFactor(pts_i, pts_j);
ResidualBlockInfo *residual_block_info = new ResidualBlockInfo(f, loss_function,
vector<double *>{para_Pose[imu_i], para_Pose[imu_j], para_Ex_Pose[0], para_Feature[feature_index]},//Optimization variables
vector<int>{0, 3});//The reason for 0 and 3 is, para_Pose[imu_i] is the pose of the first frame, which needs marg off, and 3 is para_Feature[feature_index] is the feature point related to the first frame, which needs to be marginated
marginalization_info->addResidualBlockInfo(residual_block_info);
}
}
}
}
The method of adding residuals and optimization variables above is similar to that in the back-end linear optimization, because the edge class should be written after ceres. We can simply analyze the above operations;
The first step is to define the loss function. For a priori residuals, it is the MarginalizationFactor, for IMU, and for vision, it is the ProjectionTdFactor. The classes of these three loss functions are inherited from ceres's loss function class ceres::CostFunction, which are overloaded with functions;
virtual bool Evaluate(double const *const *parameters, double *residuals, double **jacobians) const;
This function passes in the optimization variable value parameters, And the a priori value (for a priori residual, it is the a priori residual of the previous time, last_marginalization_info, for IMU, it is the estimated score, pre_integrations[1], for vision, it is the pixel coordinates of space, pts_i, pts_j). The residuals of each residual value can be calculated, as well as the Jacobian matrix of the optimization variables corresponding to the residual.
The second step is to define ResidualBlockInfo, whose constructor is as follows
ResidualBlockInfo(ceres::CostFunction *_cost_function, ceres::LossFunction *_loss_function, std::vector<double *> _parameter_blocks, std::vector<int> _drop_set)
This step is to integrate different loss functions_ cost_function and optimization variables_ parameter_blocks are unified and added to marginalization together_ Info. Variable_ loss_function is a kernel function. In the marginalization of vins mono, only the visual residual is used to the couchy kernel function. In addition, the position of the optimization variable to be used by the edge call will be set_ drop_set, there will be differences for different loss functions:
- For a priori loss, the optimization variable to be marginalized is based on whether it is equal to para_Pose[0] or para_SpeedBias[0], that is to say, the optimization variables related to the first frame are regarded as the marginalized objects;
- For IMU, its input_ drop_set is vector{0, 1}, that is, its variable to be marginalized is para_Pose[0], para_SpeedBias[0], which is also the first political related variable, is used as the object of marginalization. It is worth noting that unlike the back-end optimization, only the related variables of the first frame and the second frame are added as the optimization variables, so the information matrix constructed by marginalization will be smaller than that constructed by the back-end optimization;
- For vision, its input_ drop_set is vector{0, 3}, that is, its variable to be marginalized is para_Pose[imu_i] and para_Feature[feature_index], it can be seen from here that the edge operation of vins mono will not only edge the optimization variables related to the first frame, but also edge the road punctuation starting from the first frame.
The third step is to define the residual_ block_ Add info to marginalization_info, through the following sentence
marginalization_info->addResidualBlockInfo(residual_block_info);
Then you can see the implementation of addResidualBlockInfo() function as follows:
void MarginalizationInfo::addResidualBlockInfo(ResidualBlockInfo *residual_block_info)
{
factors.emplace_back(residual_block_info);
std::vector<double *> ¶meter_blocks = residual_block_info->parameter_blocks;//parameter_blocks contains variables related to marg
std::vector<int> parameter_block_sizes = residual_block_info->cost_function->parameter_block_sizes();
for (int i = 0; i < static_cast<int>(residual_block_info->parameter_blocks.size()); i++)//Here should be the optimized variable
{
double *addr = parameter_blocks[i];//Pointer to data
int size = parameter_block_sizes[i];//Because just having an address doesn't work, you also need to have the length of the data pointed to by the address
parameter_block_size[reinterpret_cast<long>(addr)] = size;//Force pointer to address of data
}
for (int i = 0; i < static_cast<int>(residual_block_info->drop_set.size()); i++)//This should be the variable to be marginalized
{
double *addr = parameter_blocks[residual_block_info->drop_set[i]];//This is the id of the variable to be marginalized
parameter_block_idx[reinterpret_cast<long>(addr)] = 0;//Store the id of the variable requiring marg in parameter_block_idx
}
}
In fact, the optimization variables and marginalization positions corresponding to different loss functions are stored in parameter_block_sizes and parameters_ block_ In IDX, note that the parameter is executed at this step_ block_ In IDX, only the key of the memory address of the optimization variable to be marginalized, and its corresponding value s are all 0;
2.4 step 2: call preMarginalize()
The number, storage location and length of optimized variables, as well as the number and storage location of variables to be optimized have been determined by calling addResidualBlockInfo(). The following needs to call preMarginalize() for preprocessing. preMarginalize() is implemented as follows:
void MarginalizationInfo::preMarginalize()
{
for (auto it : factors)//In the previous addResidualBlockInfo, different residual blocks will be added to the factor
{
it->Evaluate();//The residuals and Jacobian matrices of all state variables were calculated by polymorphism
std::vector<int> block_sizes = it->cost_function->parameter_block_sizes();
for (int i = 0; i < static_cast<int>(block_sizes.size()); i++)
{
long addr = reinterpret_cast<long>(it->parameter_blocks[i]);//Address of optimization variable
int size = block_sizes[i];
if (parameter_block_data.find(addr) == parameter_block_data.end())//parameter_block_data is the data of the whole optimization variable
{
double *data = new double[size];
memcpy(data, it->parameter_blocks[i], sizeof(double) * size);//Reopen a piece of memory
parameter_block_data[addr] = data;//The data address of the previous optimization variable is associated with the newly opened memory data
}
}
}
}
In the sentence it - > Evaluate(), it actually calls the overloaded function Evaluate() in each loss function, which was mentioned earlier
virtual bool Evaluate(double const *const *parameters, double *residuals, double **jacobians) const;
This function passes in the optimization variable value parameters, And the a priori value (for a priori residual, it is the a priori residual of the previous time, last_marginalization_info, and for IMU, it is the estimated score pre_integrations[1] , for vision, it is the pixel coordinates PTS of space_ i, pts_ j) The residuals of each residual value and the Jacobian matrix of each optimization variable corresponding to the residual can be calculated. In addition, parameter will be given here_ block_ Data assignment, here we quote the example in VINS thesis derivation and code analysis written by Mr. Cui Huakun
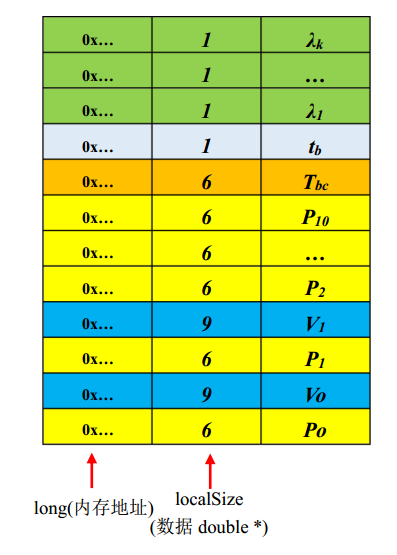
- parameter_ block_ The key value in sizes is the first column on the left in the above table, and the value value is the middle column (localSize) in the above table
- parameter_ block_ The key value in data is the first column on the left in the above table, and the value value is the first column on the right in the above table (data of double *)
2.5 step 3: call marginalize()
The data has been prepared in the previous two steps. Next, the edge operation will be officially started by calling the marginalize() function. The implementation is as follows:
void MarginalizationInfo::marginalize()
{
int pos = 0;
for (auto &it : parameter_block_idx)//Traverse the memory address of the variable to be marg optimized
{
it.second = pos;
pos += localSize(parameter_block_size[it.first]);
}
m = pos;//Number of variables to be marg dropped
for (const auto &it : parameter_block_size)
{
if (parameter_block_idx.find(it.first) == parameter_block_idx.end())//If this variable is not the optimized variable to be marg
{
parameter_block_idx[it.first] = pos;//Set the variable id to be marg to pos
pos += localSize(it.second);//pos plus the length of this variable
}
}
n = pos - m;//Number of variables to keep
//Through the above operation, all optimization variables will be pseudo sorted. The idx of the optimization variable to be marg is 0, and the others are related to the starting position
TicToc t_summing;
Eigen::MatrixXd A(pos, pos);//The size of the entire matrix A
Eigen::VectorXd b(pos);
A.setZero();
b.setZero();
TicToc t_thread_summing;
pthread_t tids[NUM_THREADS];
ThreadsStruct threadsstruct[NUM_THREADS];
int i = 0;
for (auto it : factors)//The Jacobian matrix of each residual block is allocated to each thread
{
threadsstruct[i].sub_factors.push_back(it);
i++;
i = i % NUM_THREADS;
}
for (int i = 0; i < NUM_THREADS; i++)
{
TicToc zero_matrix;
threadsstruct[i].A = Eigen::MatrixXd::Zero(pos,pos);
threadsstruct[i].b = Eigen::VectorXd::Zero(pos);
threadsstruct[i].parameter_block_size = parameter_block_size;
threadsstruct[i].parameter_block_idx = parameter_block_idx;
int ret = pthread_create( &tids[i], NULL, ThreadsConstructA ,(void*)&(threadsstruct[i]));//Construct matrices respectively
if (ret != 0)
{
ROS_WARN("pthread_create error");
ROS_BREAK();
}
}
for( int i = NUM_THREADS - 1; i >= 0; i--)
{
pthread_join( tids[i], NULL );
A += threadsstruct[i].A;
b += threadsstruct[i].b;
}
//TODO
Eigen::MatrixXd Amm = 0.5 * (A.block(0, 0, m, m) + A.block(0, 0, m, m).transpose());
Eigen::SelfAdjointEigenSolver<Eigen::MatrixXd> saes(Amm);
Eigen::MatrixXd Amm_inv = saes.eigenvectors() * Eigen::VectorXd((saes.eigenvalues().array() > eps).select(saes.eigenvalues().array().inverse(), 0)).asDiagonal() * saes.eigenvectors().transpose();
//Shure tonic
Eigen::VectorXd bmm = b.segment(0, m);
Eigen::MatrixXd Amr = A.block(0, m, m, n);
Eigen::MatrixXd Arm = A.block(m, 0, n, m);
Eigen::MatrixXd Arr = A.block(m, m, n, n);
Eigen::VectorXd brr = b.segment(m, n);
A = Arr - Arm * Amm_inv * Amr;
b = brr - Arm * Amm_inv * bmm;//A and b here should be marg's a and b, and the size has changed
//Here is the update a priori residual term
Eigen::SelfAdjointEigenSolver<Eigen::MatrixXd> saes2(A);//Find eigenvalue
Eigen::VectorXd S = Eigen::VectorXd((saes2.eigenvalues().array() > eps).select(saes2.eigenvalues().array(), 0));
Eigen::VectorXd S_inv = Eigen::VectorXd((saes2.eigenvalues().array() > eps).select(saes2.eigenvalues().array().inverse(), 0));
Eigen::VectorXd S_sqrt = S.cwiseSqrt();
Eigen::VectorXd S_inv_sqrt = S_inv.cwiseSqrt();
}
The first step is to adhere to the syntax of "add as you go" and "assign as you go" in the map data structure. The above code will first supplement the parameter_block_idx, as mentioned earlier, only the marginal optimization variables are in parameter through addResidualBlockInfo() function_ block_ IDX has a key value. Here, the memory address of the reserved optimization variable will be added as the key value, and their value value will be unified as the parameter that has been put in front of it_ block_ The sum of the dimensions of the optimization variables of IDX. At the same time, the accounting calculates two variables m and n, which are the sum of the dimensions of the optimization variables to be marginalized and the sum of the dimensions of the reserved optimization variables.
In the second step, the function will quickly construct the information matrix of each optimization variable corresponding to each residual through multithreading (Jacobi and residual have been calculated earlier), and then add it up, as shown in the following figure:
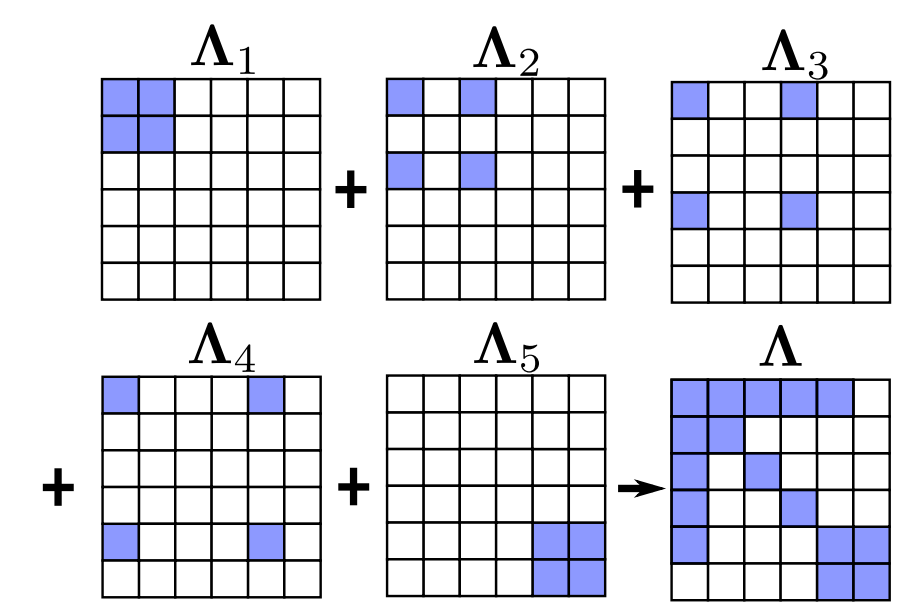
Because the parameter is used to construct the information matrix here_ block_ IDX is used as the construction order, so it will naturally construct the variables to be marginalized in the upper left of the matrix.
In the third step, the function will be marginalized by shur complement operation, and then the Jacobian matrix will be restored from the marginalized information matrix_ Jacobians and residuals linearized_residuals, these two will be brought into the next round of Jacobian and residual calculation of a priori residuals as a priori residuals.
2.6 step 4: pre movement of sliding window
At the end of optimization, there will be a sliding window pre movement operation, which is the following code
std::unordered_map<long, double *> addr_shift;
for (int i = 1; i <= WINDOW_SIZE; i++)//Start from 1, because the state of the first frame is not
{
//The operation in this step means that the contents of i-1 are stored in the position i, which means that the window moves forward one grid
addr_shift[reinterpret_cast<long>(para_Pose[i])] = para_Pose[i - 1];//So para_ These variables are double pointer variables, so this step is pointer operation
addr_shift[reinterpret_cast<long>(para_SpeedBias[i])] = para_SpeedBias[i - 1];
}
for (int i = 0; i < NUM_OF_CAM; i++)
addr_shift[reinterpret_cast<long>(para_Ex_Pose[i])] = para_Ex_Pose[i];
if (ESTIMATE_TD)
{
addr_shift[reinterpret_cast<long>(para_Td[0])] = para_Td[0];
}
vector<double *> parameter_blocks = marginalization_info->getParameterBlocks(addr_shift);
if (last_marginalization_info)
delete last_marginalization_info;//Delete the previous marg related content
last_marginalization_info = marginalization_info;//Recursion of marg related content
last_marginalization_parameter_blocks = parameter_blocks;//Optimize the recursion of variables, which are just pointers
It should be noted that this is only equivalent to moving the pointer once, and the data corresponding to the pointer is still old data. Therefore, the real sliding window movement can be realized in combination with the slideway() function called later. In addition, last_marginalization_info is the retained a priori residual information, including the retained Jacobi linearized_jacobians, residual linearized_residuals, retained data length related to marginalization, keep_block_size and order keep_block_idx and data keep_block_data.
last_marginalization_info is all the optimization variables in the reserved sliding window
Here, we need to clarify the concept that the marginalization operation does not change the value of the optimization variables, but only changes the relationship between the optimization variables, which is reflected through the information matrix.