This period of time brushed the letcode, the fun of programming may be `It's there, and you're going to conquer it'(Hahaha), there's a strange pleasure when you brush a question!

This article records an algorithmic problem I brushed and went through a process of continuous optimization and improvement and ultimately "climbing the top".

Topic priority: letcode-44_Wildcard Matching

Questions: My Questions

'?'can match any single character.
'*'can match any string (including empty strings).

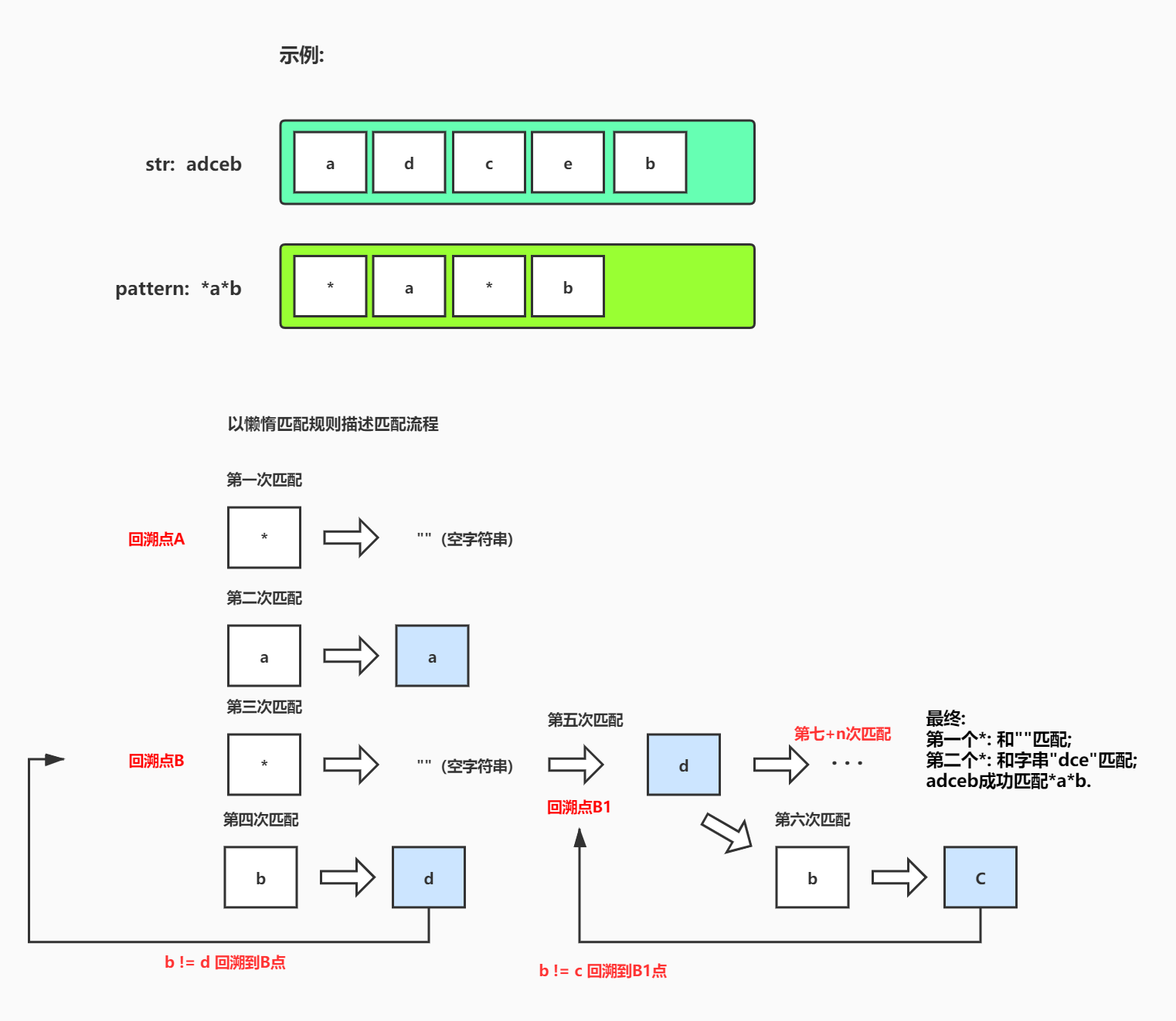
Example: (Copied from letcode)

Input:
s = "aa"
p = "a"
Output: false
 Interpretation:'a'cannot match the entire string of'a a'.


Input:
s = "aa"
p = "*"
Output: true
 Interpretation:'*'can match any string.


Input:
s = "cb"
p = "?a"
Output: false
 Interpretation:'?'can match'c', but the second'a' cannot match'b'.


Input:
s = "adceb"
p = "*a*b"
Output: true
 Interpretation: The first'*'matches an empty string, and the second'*' matches the string'dce'.


Input:
s = "acdcb"
p = "a*c?b"
Input: false

*Matching strings are uncertain, but we don't necessarily have to traverse all the possibilities (pruning) to find a successful pattern matching str;

Compared to * takes up only one character space (definitely), so any one character (where the character refers to [a-zA-Z0-9_]) can match?; any string can match * (including empty strings). (Students who know the rules should know greedy matching and lazy matching, list the two terms first, which will be reflected later in the algorithm.)

If the patterns contain *, each possible case needs to be traversed until a solution is found, and if the patterns do not contain *, only the characters corresponding to the position on the patterns and str need to be compared. Can match any character without backtracking.

Examples of matching flowcharts with * in pattern s: (Show core algorithms with lazy matching examples)

However, by constructing special patterns and strs, the computation time of the process increases exponentially (learn about regular expression injection); therefore, the patterns need to be optimized and the impossible branches removed.

Show me my submission list first (there have been 5 optimizations around)

v0.1 version

func sMatch(pattern, str []rune) bool {
    if len(str) <= 0 {
        if len(pattern) <= 0 {
            return true
        }
        for _, c := range pattern {
            if c != '*' {
                return false
            }
        }
        return true
    }
    if len(pattern) <= 0 {
        return false
    }
    sl := len(str)
    pIndex := 0
    i := 0
    for i = 0; i < sl; i++ {
        if pIndex >= len(pattern) {
            break
        }
        switch pattern[pIndex] {
        case '*':
            gl := sl
            flag := false
            for gl >= i && gl >= 0{
                if sMatch(pattern[pIndex+1:], str[gl:]) {
                    flag = true
                    break
                }
                gl-- //Discard one
            }
            return flag
        case '?':
            pIndex++
        default:
            if str[i] != pattern[pIndex] {
                return false
            }
            pIndex++
        }
    }
    if i == len(str) && pIndex != len(pattern) {
        for i := pIndex; i < len(pattern); i++ {
            if pattern[i] != '*' {
                return false
            }
        }
        return true
    }
    if pIndex != len(pattern) || i != len(str) {
        return false
    }
    return true
}

func isMatch(s string, p string) bool {
    if len(s) <= 0 {
        if len(p) <= 0 {
            return true
        }
        for _, c := range p {
            if c != '*' {
                return false
            }
        }
        return true
    }
    if len(p) <= 0 {
        return false
    }
    return sMatch([]rune(p), []rune(s))
}

Dead on this case:

str: "bbbababbbbabbbbababbaaabbaababbbaabbbaaaabbbaaaabb"
pattern: "*b********bb*b*bbbbb*ba"

v0.1 backtraces with greedy matching rules, then changes the algorithm to lazy matching rules, and passes through the case successfully

v0.2 version

```ellipsis
        case '*':
            gl := i
            flag := false
            for gl < sl{
                if pIndex == len(pattern)-1 {
                    return true
                }
                if sMatch(pattern[pIndex+1:], str[gl:]) {
                    flag = true
                    break
                }
                gl++ //I want one.
            }
            return flag
```ellipsis

However, he died on this case:

str: "aaaabaaaabbbbaabbbaabbaababbabbaaaababaaabbbbbbaabbbabababbaaabaabaaaaaabbaabbbbaababbababaabbbaababbbba"
pattern: "*****b*aba***babaa*bbaba***a*aaba*b*aa**a*b**ba***a*a*"

Suddenly, I think that connecting multiple * is not equal to a single * (a** <=> a*is a truth)

Version v0.3

``` ellipsis
    nPattern := make([]rune, 0, len(p))
    flag := false
    for _, v := range p {
        if v == '*' && flag {
            continue
        }
        if v == '*' {
            flag = true
        } else {
            flag = false
        }
        nPattern = append(nPattern, v)
    }
    return sMatch(nPattern, []rune(s))
```ellipsis

Think about this response to OK (it's torturing enough, thanks to case there would be no optimization below)

case: Change here, timeout (What!!!!)

str: "abbabaaabbabbaababbabbbbbabbbabbbabaaaaababababbbabababaabbababaabbbbbbaaaabababbbaabbbbaabbbbababababbaabbaababaabbbababababbbbaaabbbbbabaaaabbababbbbaababaabbababbbbbababbbabaaaaaaaabbbbbaabaaababaaaabb"
pattern: "**aa*****ba*a*bb**aa*ab****a*aaaaaa***a*aaaa**bbabb*b*b**aaaaaaaaa*a********ba*bbb***a*ba*bb*bb**a*b*bb"

Finally, I discovered (I actually knew at first, but didn't know how to behave), that non- * substrings in pattern s must exist in str, or they must fail to match!

Version v0.4 was born

func prepareMatch(pattern, str string) bool {
    p1 := strings.Replace(pattern, "?", "*", len(pattern))
    p2 := strings.Split(p1, "*")
    if len(p2) > 1 {
        for _, v := range p2 {
            if v == "" {
                continue
            }
            if strings.Count(p1, v) > strings.Count(str, v) {
                return false
            }
        }
    }
    return true
}


```ellipsis
    if !prepareMatch(p, s) {
        return false
    }
    return sMatch(nPattern, []rune(s))
```ellipsis

In fact, this version of optimization has some minor flaws. The general meaning of optimization is that substrings in pattern s that are not *? Should appear as many times as they appear in str, but I ignored the order in which they appeared before, so another case let me timeout

str: "aaaaaabbaabaaaaabababbabbaababbaabaababaaaaabaaaabaaaabababbbabbbbaabbababbbbababbaaababbbabbbaaaaaaabbaabbbbababbabbaaabababaaaabaaabaaabbbbbabaaabbbaabbbbbbbaabaaababaaaababbbbbaabaaabbabaabbaabbaaaaba"
pattern: "*bbb**a*******abb*b**a**bbbbaab*b*aaba*a*b**a*abb*aa****b*bb**abbbb*b**bbbabaa*b**ba**a**ba**b*a*a**aaa"

You don't know who sees this case. Did you find that the end strings of the pattern and str don't match, but v0.5 was finally born because the matching order was from there, even if the final match failed, the program would try all the possibilities in a foolish way (by the way, the minor flaw in v0.4 was fixed).

v0.5 (final version)

func prepareMatch(pattern, str string) bool {
    p1 := strings.Replace(pattern, "?", "*", len(pattern))
    p2 := strings.Split(p1, "*")
    cs := str
    //First step preprocessing
    if len(p2) > 1 {
        for _, v := range p2 {
            if v == "" {
                continue
            }
            if i := strings.Index(cs, v); i < 0 {
                return false
            } else {
                cs = cs[i+len(v):]
            }
        }
    }
    //Step 2 Preprocessing
    if pattern[len(pattern)-1] != '*' && len(p2) > 2{
        if !strings.HasSuffix(str, p2[len(p2)-1]) {
            return false;
        }
    }
    return true
}

Two problems with v0.4 have been optimized

The pleasure of programming may still be the process of continuing to solve problems with running programs!

Full Absolute Version

import "strings"

func sMatch(pattern, str []rune) bool {
    if len(str) <= 0 {
        if len(pattern) <= 0 {
            return true
        }
        for _, c := range pattern {
            if c != '*' {
                return false
            }
        }
        return true
    }
    if len(pattern) <= 0 {
        return false
    }
    sl := len(str)
    pIndex := 0
    i := 0
    for i = 0; i < sl; i++ {
        if pIndex >= len(pattern) {
            break
        }
        switch pattern[pIndex] {
        case '*':
            gl := i
            flag := false
            for gl < sl{
                if pIndex == len(pattern)-1 {
                    return true
                }
                if sMatch(pattern[pIndex+1:], str[gl:]) {
                    flag = true
                    break
                }
                gl++ //I want one.
            }
            return flag
        case '?':
            pIndex++
        default:
            if str[i] != pattern[pIndex] {
                return false
            }
            pIndex++
        }
    }
    if i == len(str) && pIndex != len(pattern) {
        for i := pIndex; i < len(pattern); i++ {
            if pattern[i] != '*' {
                return false
            }
        }
        return true
    }
    if pIndex != len(pattern) || i != len(str) {
        return false
    }
    return true
}

//optimization
func prepareMatch(pattern, str string) bool {
    p1 := strings.Replace(pattern, "?", "*", len(pattern))
    p2 := strings.Split(p1, "*")
    cs := str
    //First step preprocessing
    if len(p2) > 1 {
        for _, v := range p2 {
            if v == "" {
                continue
            }
            if i := strings.Index(cs, v); i < 0 {
                return false
            } else {
                cs = cs[i+len(v):]
            }
        }
    }
    //Step 2 Preprocessing
    if pattern[len(pattern)-1] != '*' && len(p2) > 2{
        if !strings.HasSuffix(str, p2[len(p2)-1]) {
            return false;
        }
    }
    return true
}

func isMatch(s string, p string) bool {
    if len(s) <= 0 {
        if len(p) <= 0 {
            return true
        }
        for _, c := range p {
            if c != '*' {
                return false
            }
        }
        return true
    }
    if len(p) <= 0 {
        return false
    }
    nPattern := make([]rune, 0, len(p))
    flag := false
    for _, v := range p {
        if v == '*' && flag {
            continue
        }
        if v == '*' {
            flag = true
        } else {
            flag = false
        }
        nPattern = append(nPattern, v)
    }
    if !prepareMatch(p, s) {
        return false
    }
    return sMatch(nPattern, []rune(s))
}