1 recursively reverse the entire linked list
For recursive algorithms, the most important thing is to clarify the definition of recursive functions. Specifically, our reverse function is defined as follows:
Enter a node head,take「with head As the starting point」The linked list of is inverted and returns the head node after inversion.
Understand the definition of function, and then look at this problem. For example, we want to reverse the linked list:
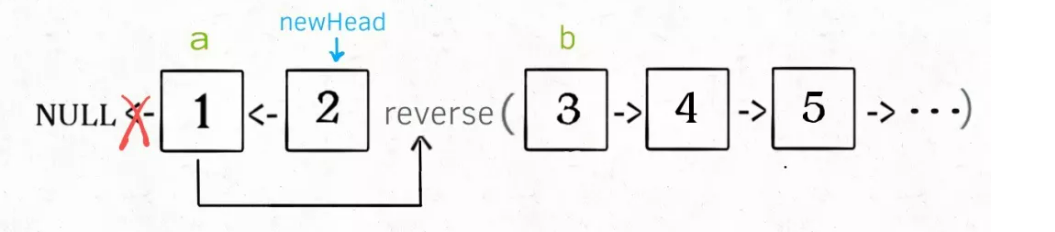
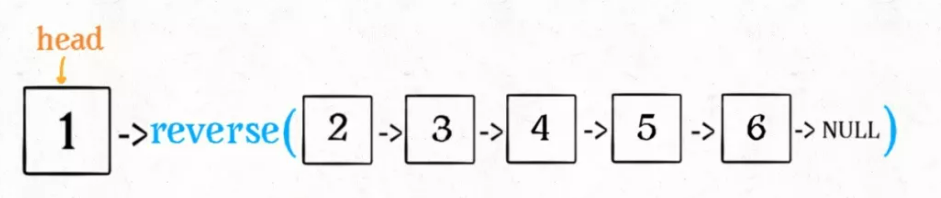
After entering reverse(head), recursion will be performed here: don't jump into recursion, but find out what results this code will produce according to the function definition just now:
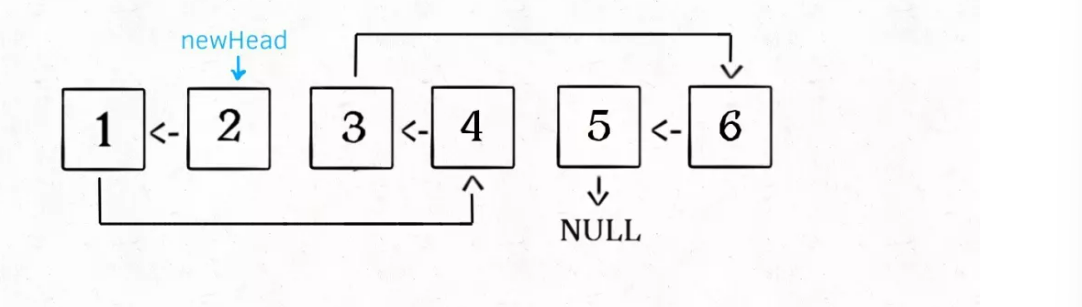
By definition, after the reverse(head.next) is executed, the entire linked list should look like this:
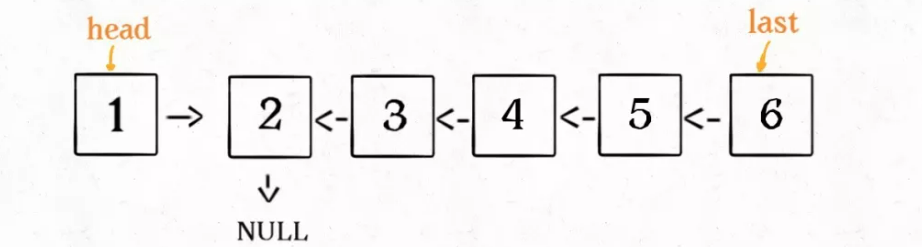
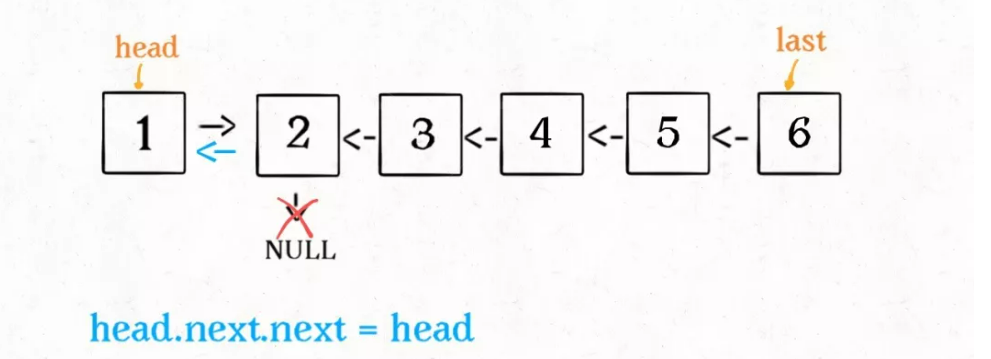
According to the function definition, the reverse function will return the inverted header node. We received it with the variable last:
head.next.next = head;
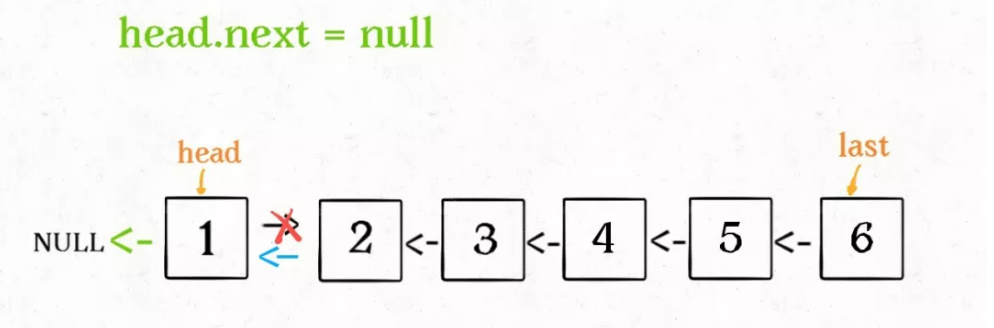
head.next = null; return last;
Recursive functions should have base case, that is, this sentence:
if (head.next == null) return head;
/**
* Definition for singly-linked list.
* public class ListNode {
* int val;
* ListNode next;
* ListNode() {}
* ListNode(int val) { this.val = val; }
* ListNode(int val, ListNode next) { this.val = val; this.next = next; }
* }
*/
class Solution {
public ListNode reverseList(ListNode head) {
if (head == null || head.next == null) {
return head;
}
ListNode newHead = reverseList(head.next);
head.next.next = head;
head.next = null;
return newHead;
}
}
2 recursively reverse the first N nodes of the linked list
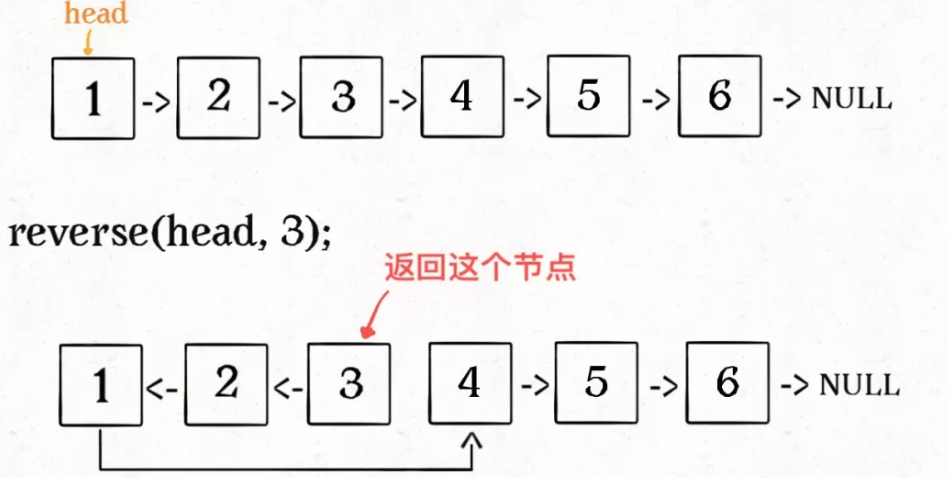
ListNode successor = null; // Rear drive node
// Invert n nodes starting from head and return a new head node
ListNode reverseN(ListNode head, int n) {
if (n == 1) {
// Record node n + 1
successor = head.next;
return head;
}
// Head Next is the starting point, and the first n - 1 nodes need to be reversed
ListNode last = reverseN(head.next, n - 1);
head.next.next = head;
// Connect the inverted head node with the following node
head.next = successor;
return last;
}
base case changes to n == 1, inverts an element, that is, itself, and records the back drive node at the same time.
Just now we just put the head Next is set to null because the original head becomes the last node of the whole linked list after the whole linked list is reversed. However, now the head node is not necessarily the last node after recursive inversion, so it is necessary to record the rear drive success (n + 1 node) and connect the head after inversion.
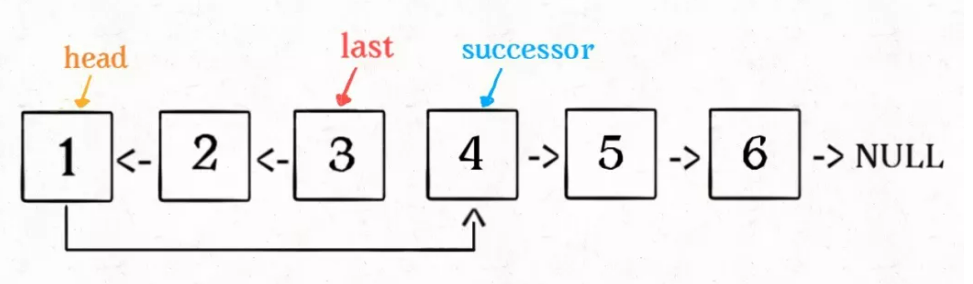
3 part of recursive reverse linked list
ListNode reverseBetween(ListNode head, int m, int n)
First, if m == 1, it is equivalent to reversing the n elements at the beginning of the linked list, which is the function we just implemented:
ListNode reverseBetween(ListNode head, int m, int n) {
// base case
if (m == 1) {
// Equivalent to inverting the first n elements
return reverseN(head, n);
}
// ...
}
If m= What should I do? If we regard the index of head as 1, we want to reverse from the m-th element, right; If you put head What if the index of next is regarded as 1? So relative to head Next, the inverted interval should start from the m - 1 element; So for head next. What about next
Different from the iterative idea, this is the recursive idea, so we can complete the code:
ListNode reverseBetween(ListNode head, int m, int n) {
// base case
if (m == 1) {
return reverseN(head, n);
}
// Advancing to the starting point of inversion triggers base case
head.next = reverseBetween(head.next, m - 1, n - 1);
return head;
}
4 recursive k a set of inverted linked lists
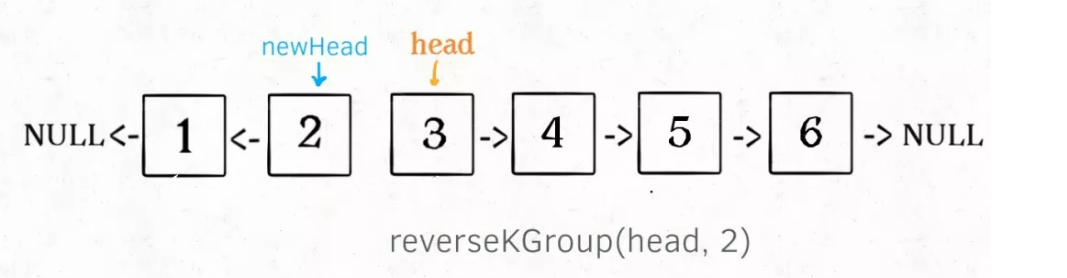
reverseKGroup(head, 2), i.e. the reverse linked list with two nodes as a group:
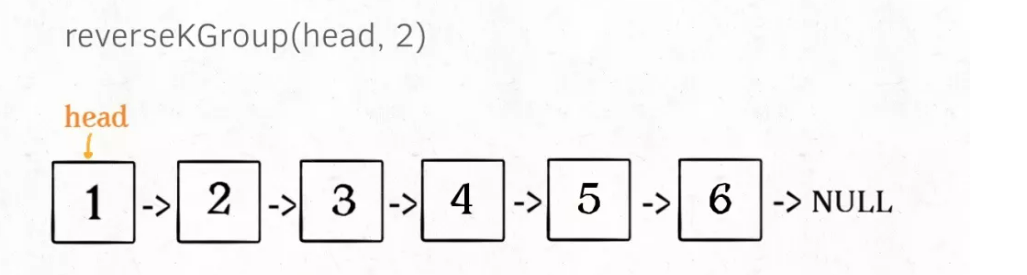
If I try to reverse the first two nodes, what about the later nodes? The latter nodes are also a linked list, and the scale (length) is smaller than the original linked list, which is called sub problem.
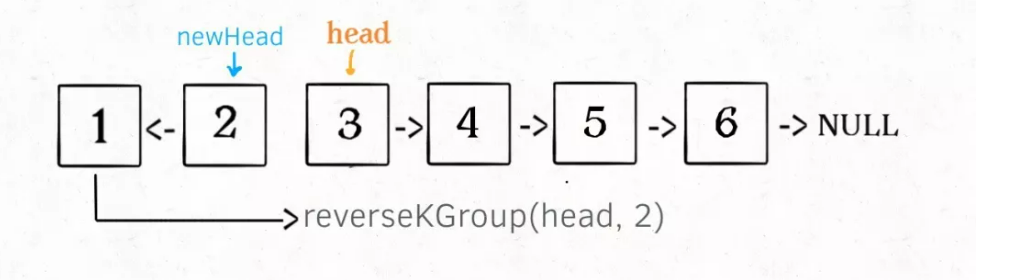
We can directly call reverseKGroup(head, 2) recursively, because the structure of the subproblem is exactly the same as that of the original problem, which is the so-called recursive property. After discovering the recursive nature, we can get the general algorithm flow:
1. First reverse the k elements starting with head:
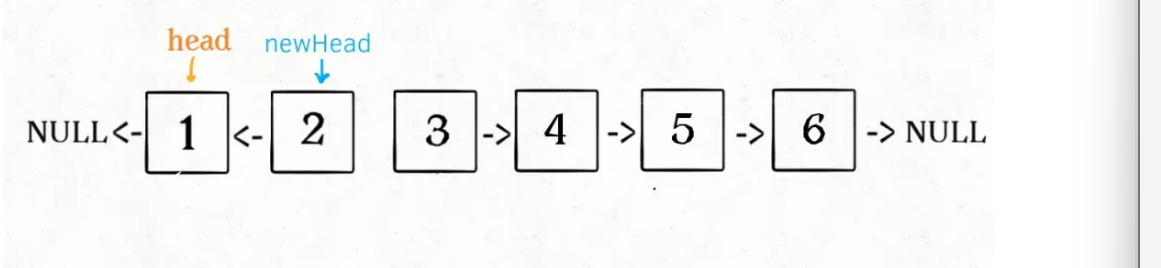
2. Recursively call the reverseKGroup function with the k + 1 element as head:
3. Connect the results of the above two processes:
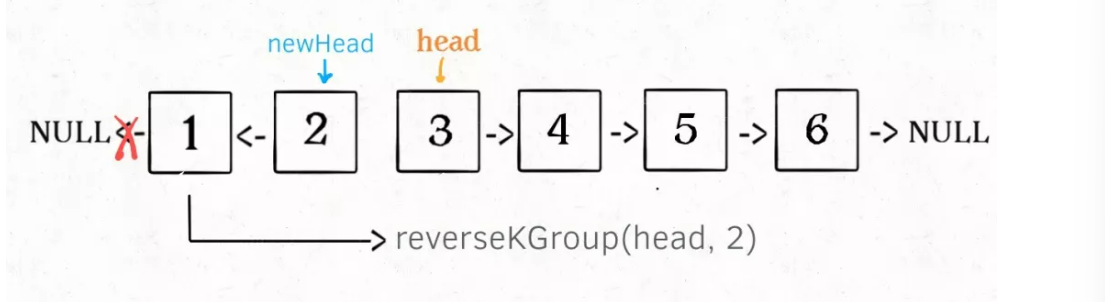
If the last element is less than k, it remains unchanged. This is the base case.
Reverse the entire linked list:
// Reverse the linked list with a as the head node
ListNode reverse(ListNode a) {
ListNode pre, cur, nxt;
pre = null; cur = a; nxt = a;
while (cur != null) {
nxt = cur.next;
// Node by node inversion
cur.next = pre;
// Update pointer position
pre = cur;
cur = nxt;
}
// Returns the inverted header node
return pre;
}
"Reversing the linked list with a as the head node" is actually "reversing the nodes between a and null". If you want to "reverse the nodes between a and b":
/** Invert the elements of interval [a, b). Note that it is closed left and open right */
ListNode reverse(ListNode a, ListNode b) {
ListNode pre, cur, nxt;
pre = null; cur = a; nxt = a;
// Just change the condition of while termination
while (cur != b) {
nxt = cur.next;
cur.next = pre;
pre = cur;
cur = nxt;
}
// Returns the inverted header node
return pre;
}
Now we have iteratively realized the function of reversing part of the linked list. Next, write the reverseKGroup function according to the previous logic:
ListNode reverseKGroup(ListNode head, int k) {
if (head == null) return null;
// The interval [a, b) contains k elements to be reversed
ListNode a, b;
a = b = head;
for (int i = 0; i < k; i++) {
// Less than k, no need to reverse, base case
if (b == null) return head;
b = b.next;
}
// Reverse the first k elements
ListNode newHead = reverse(a, b);
// Recursively invert the following linked lists and connect them
a.next = reverseKGroup(b, k);
return newHead;
}
Explain the code after the for loop. Note that the reverse function reverses the interval [a, b), so the situation is as follows: