DQN introduction
DQN(Deep Q-Learning)It is the combination of deep learning and reinforcement learning Q-table He is too big to build words to use DQN Is a good choice.
DQN algorithm mainly uses experience replay (experience pool) to realize the convergence of value function.
The Deep Q-learning method is used to iteratively update Q (s, a) with the reward obtained from each episode In dqn algorithm, (the specific method will be described later) store the (s,a,r,a ') used in each episode in M, and then extract the mini batch conversion from m to minimize the loss function.
The specific measures are:
- Individuals can remember the past state transition experience. For each state transition in each complete state sequence, according to the current state S t \begin{array}{c} S_{t} \end{array} St value chooses a behavior with a greedy strategy a t \begin{array}{c} a_{t} \end{array} at, you will be rewarded for performing this behavior R t + 1 \begin{array}{c} R_{t+1} \end{array} Rt+1 and next state S t + 1 \begin{array}{c} S_{t+1} \end{array} St+1, store the obtained state in memory
- When the capacity stored in the memory is large enough, a certain number of state transitions are randomly extracted from the memory, and the target value of the current state is calculated with the next state in the state transition
- Use the following formula to calculate the mean square cost between the target value and the network output value, and use the small block gradient descent algorithm to update the parameters of the network.
 Algorithm flow:
Algorithm flow:
Specific code implementation:
class DeepQNetwork:
def __init__(
self,
n_actions,
n_features,
learning_rate=0.01,
reward_decay=0.9,
e_greedy=0.9,
replace_target_iter=300,
memory_size=500,
batch_size=32,
e_greedy_increment=None,
output_graph=True,
):
self.n_actions = n_actions
self.n_features = n_features
self.lr = learning_rate
self.gamma = reward_decay
self.epsilon_max = e_greedy
self.replace_target_iter = replace_target_iter
self.memory_size = memory_size
self.batch_size = batch_size
self.epsilon_increment = e_greedy_increment
self.epsilon = 0 if e_greedy_increment is not None else self.epsilon_max
# Count training times
self.learn_step_counter = 0
# Initialize memory [s, a, r, s_]
self.memory = np.zeros((self.memory_size, n_features * 2 + 2))
# There are two networks [target_net, evaluate_net]
self._build_net()
t_params = tf.get_collection('target_net_params')
e_params = tf.get_collection('eval_net_params')
self.replace_target_op = [tf.assign(t, e) for t, e in zip(t_params, e_params)]
self.sess = tf.Session()
if output_graph:
# Open tensorboard
# $ tensorboard --logdir=logs
# tf.train.SummaryWriter soon be deprecated, use following
tf.summary.FileWriter(r'D:\logs', self.sess.graph)
self.sess.run(tf.global_variables_initializer())
self.cost_his = []
def _build_net(self):
# --------------Create eval neural network and improve parameters in time--------------
self.s = tf.placeholder(tf.float32, [None, self.n_features], name='s') # Used to receive observation
self.q_target = tf.placeholder(tf.float32, [None, self.n_actions],
name='Q_target') # Used to receive Q_ The value of target, which will be calculated later
with tf.variable_scope('eval_net'):
# c_names(collections_names) is updating the target_net parameter
c_names, n_l1, w_initializer, b_initializer = \
['eval_net_params', tf.GraphKeys.GLOBAL_VARIABLES], 10, \
tf.random_normal_initializer(0., 0.3), tf.constant_initializer(0.1) # config of layers
# eval_net collections is updating the target_net parameter
with tf.variable_scope('l1'):
w1 = tf.get_variable('w1', [self.n_features, n_l1], initializer=w_initializer, collections=c_names)
b1 = tf.get_variable('b1', [1, n_l1], initializer=b_initializer, collections=c_names)
l1 = tf.nn.relu(tf.matmul(self.s, w1) + b1)
# eval_net collections is updating the target_net parameter
with tf.variable_scope('l2'):
w2 = tf.get_variable('w2', [n_l1, self.n_actions], initializer=w_initializer, collections=c_names)
b2 = tf.get_variable('b2', [1, self.n_actions], initializer=b_initializer, collections=c_names)
self.q_eval = tf.matmul(l1, w2) + b2
with tf.variable_scope('loss'): # Seek error
self.loss = tf.reduce_mean(tf.squared_difference(self.q_target, self.q_eval))
with tf.variable_scope('train'): # gradient descent
self._train_op = tf.train.RMSPropOptimizer(self.lr).minimize(self.loss)
# ----------------Create target neural network and provide target Q---------------------
self.s_ = tf.placeholder(tf.float32, [None, self.n_features], name='s_') # Receive next observation
with tf.variable_scope('target_net'):
# c_names(collections_names) is updating the target_net parameter
c_names = ['target_net_params', tf.GraphKeys.GLOBAL_VARIABLES]
# target_net collections is updating the target_net parameter
with tf.variable_scope('l1'):
w1 = tf.get_variable('w1', [self.n_features, n_l1], initializer=w_initializer, collections=c_names)
b1 = tf.get_variable('b1', [1, n_l1], initializer=b_initializer, collections=c_names)
l1 = tf.nn.relu(tf.matmul(self.s_, w1) + b1)
# target_net collections is updating the target_net parameter
with tf.variable_scope('l2'):
w2 = tf.get_variable('w2', [n_l1, self.n_actions], initializer=w_initializer, collections=c_names)
b2 = tf.get_variable('b2', [1, self.n_actions], initializer=b_initializer, collections=c_names)
self.q_next = tf.matmul(l1, w2) + b2
def store_transition(self, s, a, r, s_):
# Judge whether the corresponding attribute is included, and assign the initial value if it is not included
if not hasattr(self, 'memory_counter'):
self.memory_counter = 0
# Longitudinal extension
transition = np.hstack((s, [a, r], s_))
# Replace the memory of the old network with a new one
index = self.memory_counter % self.memory_size
self.memory[index, :] = transition
self.memory_counter += 1
def choose_action(self, observation):
# Add batch to the observation_ Size dimension
observation = observation[np.newaxis, :]
if np.random.uniform() < self.epsilon:
# forward feed the observation and get q value for every actions
actions_value = self.sess.run(self.q_eval, feed_dict={self.s: observation})
action = np.argmax(actions_value)
else:
action = np.random.randint(0, self.n_actions)
return action
def learn(self):
# Determine whether the target net network should be updated
if self.learn_step_counter % self.replace_target_iter == 0:
self.sess.run(self.replace_target_op)
print('\ntarget_params_replaced\n')
# Randomly extract some memories from previous memories
if self.memory_counter > self.memory_size:
sample_index = np.random.choice(self.memory_size, size=self.batch_size)
else:
sample_index = np.random.choice(self.memory_counter, size=self.batch_size)
batch_memory = self.memory[sample_index, :]
q_next, q_eval = self.sess.run(
[self.q_next, self.q_eval],
feed_dict={
self.s_: batch_memory[:, -self.n_features:], # fixed params
self.s: batch_memory[:, :self.n_features], # newest params
})
# change q_target w.r.t q_eval's action
q_target = q_eval.copy()
# The following steps are very important q_next, q_eval contains the values of all action s,
# What we need is the selected action value, and others are not needed
# Therefore, we change all other action values to 0, and pass back the action error value used as the update credential
# This is what we finally want to achieve, such as q_target - q_eval = [1, 0, 0] - [-1, 0, 0] = [2, 0, 0]
# q_eval = [-1, 0, 0] indicates that I have selected action 0 in this memory, and Q(s, a0) = -1 brought by action 0, so other Q(s, a1) = Q(s, a2) = 0
# q_target = [1, 0, 0] indicates R + gamma * MAXQ (s_)= 1, and no matter in S_ Which action did we take last month,
# We all need to correspond to Q_ The position of action in Eval, so 1 is placed in the position of action 0
# The following is also to achieve the above purpose, but in order to make the program operation more convenient, the process of achieving the purpose is a little different
# Yes will q_eval all assigned to q_target, then q_target-q_eval is all 0,
# But we'll do it again according to batch_ The action column in memory is used for Q_ Modify the assignment according to the corresponding memory action position in target
# Make the new assignment reward + gamma * maxQ(s_), So q_target-q_eval can become what we need
# There is another example below
batch_index = np.arange(self.batch_size, dtype=np.int32)
eval_act_index = batch_memory[:, self.n_features].astype(int)
reward = batch_memory[:, self.n_features + 1]
q_target[batch_index, eval_act_index] = reward + self.gamma * np.max(q_next, axis=1)
"""
If in this batch in, We have two extracted memories, Three can be produced according to each memory action Value of:
q_eval =
[[1, 2, 3],
[4, 5, 6]]
q_target = q_eval =
[[1, 2, 3],
[4, 5, 6]]
Then according to memory Specific action Location to modify q_target corresponding action Value on:
Like in:
Memory 0 q_target The calculated value is -1, And I used it action 0;
Memory 1 q_target The calculated value is -2, And I used it action 2:
q_target =
[[-1, 2, 3],
[4, 5, -2]]
therefore (q_target - q_eval) It becomes:
[[(-1)-(1), 0, 0],
[0, 0, (-2)-(6)]]
Finally, we will this (q_target - q_eval) As error, Back propagation neural network.
All 0 action The value was not selected at that time action, There was a choice before action There is a value that is not 0.
We only reverse the previous selection action Value of,
"""
# Training eval network
_, self.cost = self.sess.run([self._train_op, self.loss],
feed_dict={self.s: batch_memory[:, :self.n_features],
self.q_target: q_target})
self.cost_his.append(self.cost)
# Because it will gradually converge during training, the growth epsilon is dynamically set here
self.epsilon = self.epsilon + self.epsilon_increment if self.epsilon < self.epsilon_max else self.epsilon_max
self.learn_step_counter += 1
DDQN introduction
DQN algorithm has made great achievements in the field of deep reinforcement learning, but it can not guarantee the convergence all the time.
The research shows that this algorithm for estimating the target value overestimates the behavior value in some cases, resulting in the algorithm will unanimously regard the suboptimal behavior value as the optimal behavior value, and finally can not converge to the optimal value function.

Programming - DQN based on pytoch to solve PuckWorld problem
Article worth learning - Implementation of seven DQN in reinforcement learning practice
PuckWorld environment introduction:
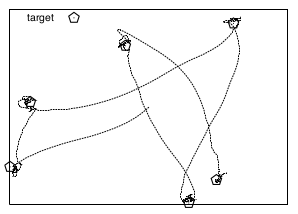
Puckworld (Ice Hockey World), in short, means that the Agent pursues the random target objects in the world.
- PuckWorld environment appears in Lecture 7 of reinforcement learning. It describes a scene in which an individual in a continuous two-dimensional space chases a target object.
- As shown in the following figure: in the rectangular space, individuals try to get as close to the pentagonal target as possible to obtain more rewards; At the same time, the target object (pentagons) will reappear at random positions in the region every certain time. Individuals need to respond to this and adjust their behavior to approach the target object in the new position.
-
- The biggest difference between this environment and the previous grid world environment is that the rectangular area is a space described by two-dimensional continuous variables. At this time, continuous values must be used to describe the position of an individual or target object.
In the classic PuckWorld environment,
The observation space of an individual consists of six variables:
- Two variables describe the individual's position (coordinate values in horizontal and vertical directions)
- Two variables describe the position of the target object (coordinate values in horizontal and vertical directions)
- The component of the speed of an individual's movement in the horizontal and vertical directions.
The individual behavior space is still a one-dimensional discrete space, with five possible values, respectively:
- Increase the unit rate values in the left, right, up and down directions
- Maintain current speed. The dynamics of the environment is reflected in that the position of the individual at the next time is determined by the current position and its speed; The target object refreshes its position randomly with a fixed period;
Actual effect:
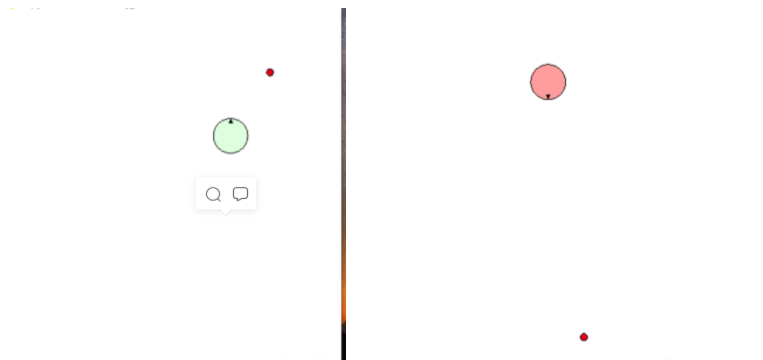
The green ball is our Agent, the red ball is our target, and it will move randomly. At the beginning, the Agent does not understand this strange environment, so it needs to continue to explore. After completing the sequence again and again, the Agent gradually understands. Finally, it can reach the goal. As soon as it sees the goal, it will rush to him, catch the goal and win the final victory.
The color of the Agent is also set. The farther away from the target, the darker the color, and the closer to the target, the lighter the color. In addition, the arrow on the small ball indicates the direction in which the current Agent performs actions in the state.
The source code will be uploaded later