
yesterday Dynamic programming: you should know this about 01 backpack! In, we use two-dimensional dp array to explain 01 knapsack.
Today, let's talk about rolling array. In fact, we have used rolling array in the previous topic, that is, reducing two-dimensional dp to one-dimensional dp. Some recording friends expressed confusion at that time.
So let's talk about rolling array thoroughly through 01 backpack!
Next, let's use the following example to explain
The maximum weight of the backpack is 4.
Items are:
weight | value | |
|---|---|---|
Item 0 | 1 | 15 |
Item 1 | 3 | 20 |
Item 2 | 4 | 30 |
What is the maximum value of the items that can be carried by the backpack?
One dimensional dp array (scrolling array)
For the knapsack problem, the state can be compressed.
When using a two-dimensional array, the recurrence formula is: dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - weight[i]] + value[i]);
In fact, it can be found that if the layer dp[i - 1] is copied to dp[i], the expression can be: dp[i][j] = max(dp[i][j], dp[i][j - weight[i]] + value[i]);
Instead of copying dp[i - 1] to dp[i], it's better to use only one-dimensional array, only dp[j] (one-dimensional array, which can also be understood as a rolling array).
This is the origin of the rolling array. The condition to be met is that the upper layer can be reused and copied directly to the current layer.
After reading this, it is estimated that everyone has forgotten what I and j in dp[i][j] express. I is an item and j is the capacity of the backpack.
dp[i][j] indicates the maximum value of taking any item with subscript [0-i] and putting it into the backpack with capacity j.
Be sure to always remember the meaning of i and j here, otherwise it's easy to be confused.
The five part analysis of dynamic gauge is as follows:
- Determine the definition of dp array
In the one-dimensional dp array, dp[j] means that for a backpack with a capacity of j, the value of the items carried can be up to dp[j].
- Recurrence formula of one-dimensional dp array
dp[j] is the maximum value carried by a backpack with a capacity of j, so how to deduce dp[j]?
dp[j] can be derived from dp[j - weight[i]], which represents the maximum value carried by a backpack with a capacity of j - weight[i].
dp[j - weight[i]] + value[i] represents the backpack with the capacity of j - the weight of item I plus the value of item I. (that is, the value of the backpack with the capacity of j after the item I is put in, i.e. dp[j])
At this time, dp[j] has two choices: one is to take its own dp[j] which is equivalent to dp[i-1][j] in the two-dimensional dp array, that is, not put the item I; the other is to take dp[j - weight[i]] + value[i], that is, put the item I, and specify to take the maximum, which is to find the maximum value after all,
So the recursive formula is:
dp[j] = max(dp[j], dp[j - weight[i]] + value[i]);
It can be seen that the writing method of two-dimensional dp array is to remove the dimension of I in dp[i][j].
- How to initialize one-dimensional dp array
As for initialization, it must be consistent with the definition of dp array, otherwise it will become more and more chaotic when it comes to recursive formula.
dp[j] means that the maximum value of the items carried by a backpack with a capacity of j can be dp[j], so dp[0] should be 0, because the maximum value of the items carried by a backpack with a capacity of 0 is 0.
So how many subscripts should be initialized in dp array except the position of subscript 0, which is initially 0?
Let's look at the recursive formula (DP I - value) [DP I];
dp array must take the largest value when deriving. If the value given by the topic is a positive integer, then the non-0 subscript can be initialized to 0.
In this way, the maximum value of dp array can be obtained in the process of recursive formula, rather than being overwritten by the initial value.
Then I assume that the value of items is greater than 0, so when initializing the dp array, it can be initialized to 0.
- Traversal order of one-dimensional dp array
The code is as follows:
for(int i = 0; i < weight.size(); i++) { // Traverse items
for(int j = bagWeight; j >= weight[i]; j--) { // Traversal knapsack capacity
dp[j] = max(dp[j], dp[j - weight[i]] + value[i]);
}
}
Here we find that the order of traversing the backpack is different from that in the writing of two-dimensional dp!
When two-dimensional dp traverses, the knapsack capacity is from small to large, while when one-dimensional dp traverses, the knapsack capacity is from large to small.
Why?
The reverse order traversal is to ensure that the item i is only put once!. But once the positive sequence is traversed, the item 0 will be added repeatedly many times!
For example, the weight[0] = 1 and the value[0] = 15 of article 0
If positive order traversal
dp[1] = dp[1 - weight[0]] + value[0] = 15
dp[2] = dp[2 - weight[0]] + value[0] = 30
At this time, dp[2] is already 30, which means that item 0 has been put in twice, so it cannot be traversed in positive order.
Why can you put items in reverse order after traversing them once?
The reverse order is to calculate dp[2] first
dp[2] = dp[2 - weight[0]] + value[0] = 15 (dp array has been initialized to 0)
dp[1] = dp[1 - weight[0]] + value[0] = 15
Therefore, in the cycle from back to front, each acquisition state will not coincide with the previous acquisition state, so each item will be taken only once.
Then the question comes again. Why don't you reverse the order of two-dimensional dp array calendars?
For two-dimensional dp, dp[i][j] is calculated from the previous layer, namely dp[i - 1][j]. dp[i][j] of this layer will not be covered!
(if you can't understand it here, you'll have a try. Fantasy is still unreliable. Practice makes true knowledge!)
Let's take a look at the order of the two nested for loops. The code first traverses the items nested and traverses the knapsack capacity. Can you traverse the knapsack capacity nested and traverses the items first?
may not!
Because of the writing of one-dimensional dp, the knapsack capacity must be traversed in reverse order (the reason has been mentioned above). If the traversal knapsack capacity is placed on the upper layer, each dp[j] will only put one item, that is, only one item is placed in the knapsack.
(if you don't understand it here, just recall the definition of dp[j], or try reversing the order of the two for loops!)
Therefore, the traversal order of the knapsack of one-dimensional dp array is very different from that of two-dimensional array!, We must pay attention to this.
- Derivation of dp array by example
One dimensional dp, use item 0, item 1 and item 2 to traverse the backpack respectively, and the final results are as follows:
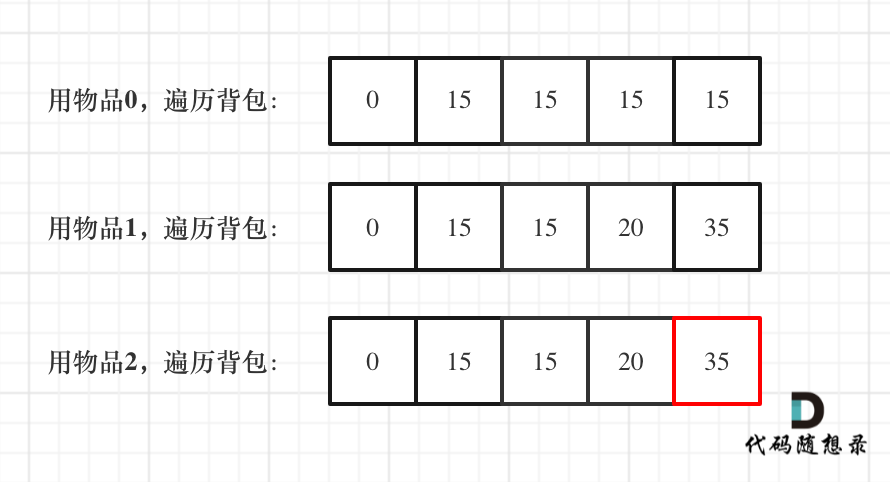
Dynamic programming knapsack problem 9
One dimensional dp01 knapsack complete C + + test code
void test_1_wei_bag_problem() {
vector<int> weight = {1, 3, 4};
vector<int> value = {15, 20, 30};
int bagWeight = 4;
// initialization
vector<int> dp(bagWeight + 1, 0);
for(int i = 0; i < weight.size(); i++) { // Traverse items
for(int j = bagWeight; j >= weight[i]; j--) { // Traversal knapsack capacity
dp[j] = max(dp[j], dp[j - weight[i]] + value[i]);
}
}
cout << dp[bagWeight] << endl;
}
int main() {
test_1_wei_bag_problem();
}
It can be seen that the 01 backpack of one-dimensional dp is much simpler than that of two-dimensional! The initialization and traversal sequence is relatively simple.
Therefore, I tend to use the writing method of one-dimensional dp array, which is more intuitive and concise, and the space complexity is reduced by an order of magnitude!
In the following explanation of knapsack problem, I directly use one-dimensional dp array for derivation.
summary
The above explanation can develop an interview question (after all, there is no original question).
This is the topic of this article. It is required to implement a pure two-dimensional 01 knapsack first. If it is written, then ask why the nesting order of two for loops is written like this? Can you write in reverse? Let's talk about the logic of initialization.
Then it is required to implement a 01 knapsack of one-dimensional array. Finally, ask, can the 01 knapsack of one-dimensional array be written in the reverse order of the two for loops? Why?
Note that the above questions are only asked when the candidate writes the code.
It is the question of pure 01 knapsack. You can see the candidate's understanding of the algorithm without taking the question of 01 knapsack application.
I believe that after reading this article, you should have answers to all the above questions!
At this time, the theoretical basis of 01 knapsack is finished. I used two articles to deeply analyze the definition, recursive formula, initialization and traversal sequence of dp array of 01 knapsack from two-dimensional array to one-dimensional array, without sparing any difficulties.
You can find that the amount of information is still quite large.
If you put dynamic programming: about 01 knapsack problem, you should know these! And the content of this article are understood. Later, when we do the topic of 01 backpack, we will find it very simple.
Instead of writing a backpack by feeling or memory, you have your own thinking and understand its essence. All aspects of the code are under your own control.
Even if the code does not pass, it will have its own logic to debug, so it will be clear.
Next, we will start to use the theoretical basis of these two days to do the backpack interview questions on the buckle. The recording friends hold the handrail tightly, and we are going to get on the highway!
Other language versions
Java
public static void main(String[] args) {
int[] weight = {1, 3, 4};
int[] value = {15, 20, 30};
int bagWight = 4;
testWeightBagProblem(weight, value, bagWight);
}
public static void testWeightBagProblem(int[] weight, int[] value, int bagWeight){
int wLen = weight.length;
//Define dp array: dp[j] represents the maximum value that can be obtained when the backpack capacity is j
int[] dp = new int[bagWeight + 1];
//Traversal order: first traverse the items, and then traverse the backpack capacity
for (int i = 0; i < wLen; i++){
for (int j = bagWeight; j >= weight[i]; j--){
dp[j] = Math.max(dp[j], dp[j - weight[i]] + value[i]);
}
}
//Print dp array
for (int j = 0; j <= bagWeight; j++){
System.out.print(dp[j] + " ");
}
}
Python
def test_1_wei_bag_problem():
weight = [1, 3, 4]
value = [15, 20, 30]
bag_weight = 4
# Initialization: all 0
dp = [0] * (bag_weight + 1)
# First traverse the items, and then traverse the backpack capacity
for i in range(len(weight)):
for j in range(bag_weight, weight[i] - 1, -1):
# Recursive formula
dp[j] = max(dp[j], dp[j - weight[i]] + value[i])
print(dp)
test_1_wei_bag_problem()
Go
func test_1_wei_bag_problem(weight, value []int, bagWeight int) int {
// Define and initialize
dp := make([]int,bagWeight+1)
// Recursive order
for i := 0 ;i < len(weight) ; i++ {
// Here, we must reverse the order and distinguish between two dimensions, because two-dimensional dp saves the state of i
for j:= bagWeight; j >= weight[i] ; j-- {
// Recurrence formula
dp[j] = max(dp[j], dp[j-weight[i]]+value[i])
}
}
//fmt.Println(dp)
return dp[bagWeight]
}
func max(a,b int) int {
if a > b {
return a
}
return b
}
func main() {
weight := []int{1,3,4}
value := []int{15,20,30}
test_1_wei_bag_problem(weight,value,4)
}
javaScript
function testWeightBagProblem(wight, value, size) {
const len = wight.length,
dp = Array(size + 1).fill(0);
for(let i = 1; i <= len; i++) {
for(let j = size; j >= wight[i - 1]; j--) {
dp[j] = Math.max(dp[j], value[i - 1] + dp[j - wight[i - 1]]);
}
}
return dp[size];
}
function test () {
console.log(testWeightBagProblem([1, 3, 4, 5], [15, 20, 30, 55], 6));
}
test();