1. Title

Give you an array and rotate the elements of the array K positions to the right, where k is a non-negative number.

Example 1:

Input: nums = [1,2,3,4,5,6,7], k = 3

Output: [5,6,7,1,2,3,4]

Explanation:

Rotate one step to the right: [7,1,2,3,4,5,6]

Rotate 2 steps to the right: [6,7,1,2,3,4,5]

Rotate 3 steps to the right: [5,6,7,1,2,3,4]

Example 2:

Input: nums = [-1,-100,3,99], k = 2

Output: [3,99, -1, -100]

Explanation:

Rotate one step to the right: [99, -1, -100,3]

Rotate 2 steps to the right: [3,99, -1, -100]

Tips:

• 1 <= nums.length <= 10^5
• -2^31 <= nums[i] <= 2^31 - 1
• 0 <= k <= 10^5

Advanced:

There are at least three different ways to think up as many solutions as possible.

Can you solve this problem using the in-place algorithm with spatial complexity O(1)?

2. Ideas

(1) When you see that elements within an array are moved, the most immediate idea is to open up a new array space where the position is moved by copying each other between the new array and the original array.

Click Execute Code and the first test case passes! (

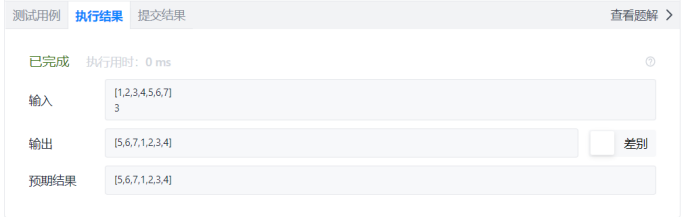
Confidence full point "submit", the result failed!

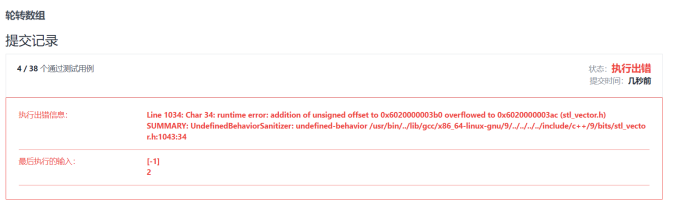
Oh!! There were cases where k was longer than or equal to the length of the array!! So just add two lines to the front

 while(n <= k)

            k-=n;

Here's a hint for writing code in the future: take special degradation into account each time

Here is the complete code

class Solution {
public:
    void rotate(vector<int>& nums, int k) {
        int n = nums.size();
        while(n <= k)
            k-=n;
        int* New_nums = new int[n];
        for(int i = 0; i < n-k;i++)
            New_nums[i + k] = nums[i];
        for(int i = n-k; i < n; i++)
            New_nums[i -(n - k)] = nums[i];
        for(int i = 0; i< n; i++)
            nums[i] = New_nums[i];
        delete []New_nums;
    }
};

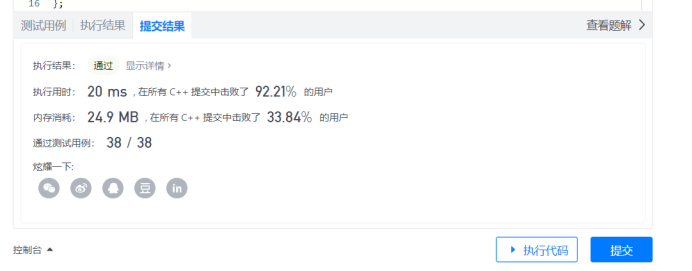
Space consumption is a bit high, there is room for improvement!

(2) If no new arrays are created, what happens in place of the original arrays?

A variable temp is introduced to store the intermediate value of the exchange, moving the last nums number to the beginning each time, and looping k times.

class Solution {
public:
    void rotate(vector<int>& nums, int k) {
        int n = nums.size();
        int temp;
        while(k--)
        {
            temp = nums[n-1];
            for(int i = n-1;i>0;i--)
                nums[i] = nums[i-1];
            nums[0] = temp;
        }
    }
};

This solves the problem of space consumption, O(1), but what about time... after all, time complexity is O(N) ²) After submitting the code, you do

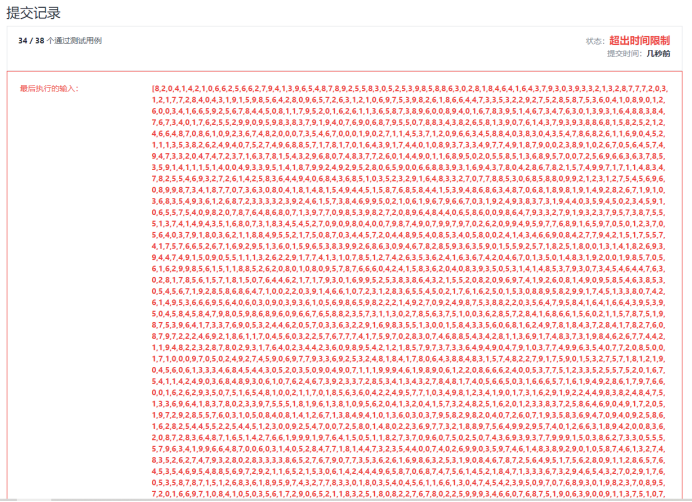
3. Official solution

Method 1: Use an extra array

We can use additional arrays to place each element in the correct position. Representing the length of the array with n, we iterate through the original array, place the element labeled i i n the new array labeled (i+k) mod n, and copy the new array to the original.

class Solution {
public:
    void rotate(vector<int>& nums, int k) {
        int n = nums.size();
        vector<int> newArr(n);
        for (int i = 0; i < n; ++i) {
            newArr[(i + k) % n] = nums[i];
        }
        nums.assign(newArr.begin(), newArr.end());
    }
};

Author: LeetCode-Solution
 Links: https://leetcode-cn.com/problems/rotate-array/solution/xuan-zhuan-shu-zu-by-leetcode-solution-nipk/
Source: Force buckle ( LeetCode)
Copyright belongs to the author. For commercial reprinting, please contact the author for authorization. For non-commercial reprinting, please indicate the source.

Complexity analysis

• Time complexity: O(n), where n is the length of the array.

• Spatial Complexity: O(n).

Method 2: Ring replacement
The reason for using extra arrays in Method 1 is that if we place each number directly at its last position, the elements in the placement will be overwritten and lost. Therefore, from another point of view, we can save the replaced elements in the variable temp, avoiding the overhead of extra arrays.

We start at position 0 and initially temp=nums[0]. According to the rule, the element at position 0 is placed at (0+k) mod n so that x = (0+k) mod n, where temp and nums[x] are exchanged to complete the update of position X. Next, we look at location x and exchange temp and nums[(x+k) mod n] to complete the update of the next location. Continue this process until you return to the initial position of 0.

It is easy to see that when we go back to the initial position of 0, some numbers may not have been traversed yet, so we should start the process of repeating from the next number, but how can we end the traversal at this time? Let's start with the question: How many elements have we traversed since 0 and then back to starting 0?

Since we have finally returned to the starting point, this process happened to take an integer number of circles, it might be better to set it as a circle; Resetting the process traversed a total of b elements. So we have an=bk, that is, an must be a common multiple of N and K. And because we end when we first get back to the starting point, A is as small as possible, so a n is the lowest common multiple lcm(n,k) of N and k, so b is lcm(n,k)/k.

This means that a single traversal will access lcm(n,k)/k elements. To access all the elements, we need to traverse the number of times

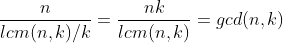
Where gcd refers to the greatest common divisor.

Let's illustrate this process more specifically with the following examples:

nums = [1,2,3,4,5,6]

k = 2

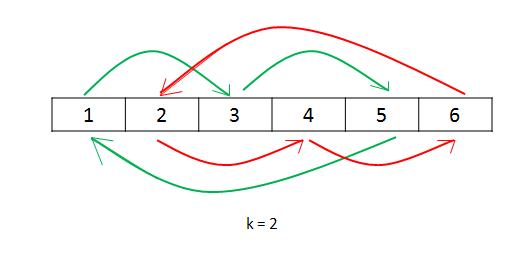
If the reader has some difficulty understanding the mathematical derivation above, there is another way to complete the code: use a separate variable count to track the number of elements currently being accessed, and end the traversal when count=n.

class Solution {
public:
    void rotate(vector<int>& nums, int k) {
        int n = nums.size();
        k = k % n;
        int count = gcd(k, n);
        for (int start = 0; start < count; ++start) {
            int current = start;
            int prev = nums[start];
            do {
                int next = (current + k) % n;
                swap(nums[next], prev);
                current = next;
            } while (start != current);
        }
    }
};

Author: LeetCode-Solution
 Links: https://leetcode-cn.com/problems/rotate-array/solution/xuan-zhuan-shu-zu-by-leetcode-solution-nipk/
Source: Force buckle ( LeetCode)
Copyright belongs to the author. For commercial reprinting, please contact the author for authorization. For non-commercial reprinting, please indicate the source.

Complexity analysis

• Time complexity: O(n), where n is the length of the array. Each element is only traversed once.

• Spatial complexity: O(1). We only need constant space for a few variables.

Method 3: Array flip
This method is based on the fact that when we move the elements of an array k times to the right, the tail kmodn elements move to the head of the array, and the remaining elements move kmodn positions backwards.

The method is to flip the array: we can flip all the elements so that the kmodn elements at the end are moved to the head of the array, and then we can flip the elements in the [0,kmodn_1] interval and the elements in the [kmodn,n_1] interval to get the final answer.

Let's take n=7, k=3 as an example to show the following:

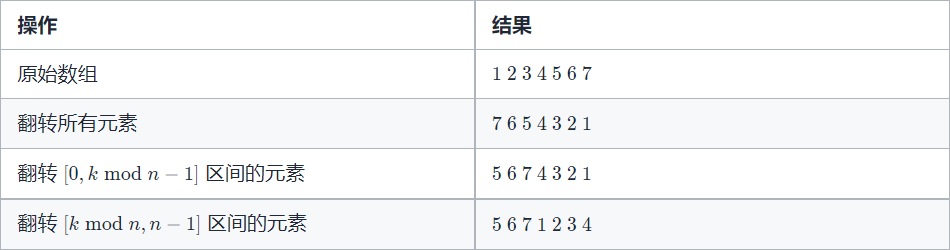
class Solution {
public:
    void reverse(vector<int>& nums, int start, int end) {
        while (start < end) {
            swap(nums[start], nums[end]);
            start += 1;
            end -= 1;
        }
    }

    void rotate(vector<int>& nums, int k) {
        k %= nums.size();
        reverse(nums, 0, nums.size() - 1);
        reverse(nums, 0, k - 1);
        reverse(nums, k, nums.size() - 1);
    }
};

Author: LeetCode-Solution
 Links: https://leetcode-cn.com/problems/rotate-array/solution/xuan-zhuan-shu-zu-by-leetcode-solution-nipk/
Source: Force buckle ( LeetCode)
Copyright belongs to the author. For commercial reprinting, please contact the author for authorization. For non-commercial reprinting, please indicate the source.

Complexity analysis

• Time complexity: O(n), where n is the length of the array. Each element is flipped twice, totaling n elements, so the total time complexity is O(2n)=O(n).
• Spatial complexity: O(1).

4. Learning Experience

1. Write the algorithm with if statement in front of the general situation, taking special or accidental situations into account. If "k is greater than the length of the array" in this question, then K%= n is required.

2. The beauty of the expression (i + k) mod n: 1) putting the interval segment nums [0, n-k] together with nums [n-k, n], there is no need to discuss them separately; 2) taking into account the case where k is greater than or equal to n, avoiding extra discussion!

3. Ring replacement of arrays. If you do not want to use extra space (declare a new array space), you can use ring replacement on the original array.