Scrambling code of OFDM

1. Purpose
In digital communication, if long 0 or 1 sequences often appear, it will affect the establishment and maintenance of bit synchronization. Using scrambling code in the transmitter can avoid the adverse effect of this data on the timing of the receiver. At the same time, in order to limit the crosstalk caused by different degrees of nonlinear characteristics in the circuit to the communication of other circuits, the minimum period of the digital signal is required to be long enough. Therefore, the requirements can be met by transforming the digital signal into a digital sequence with statistical characteristics similar to white noise, which is usually realized by scrambling. The so-called scrambling is a technology that disturbs the signal without adding redundancy and changes the statistical characteristics of digital signal to make it approximate the statistical characteristics of white noise.
2. Production principle
802.11a protocol requires scrambling of DATA domain. The DATA field includes: Service, PSDU, tail bit and fill bit. Firstly, a frame synchronization scrambler with a length of 127bit needs to scramble the DATA domain. The octet of PSDU exists in the form of sending serial bit stream, with bit 0 first and bit 7 last. The generation polynomial used by the scrambler is as follows:

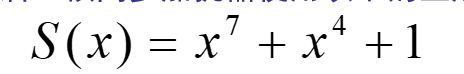
That is, the data is sent to the scrambler, which uses the generated polynomial to obtain the result and then outputs it. The output result is the result after scrambling.

The scrambler is based on the linear feedback shift register, and the generated polynomial is used to define how to calculate the output. The scrambler has a seven bit shift register, so it is necessary to define a seven bit pseudo-random processing state (composed of 0 and 1, but not all zeros), also known as scrambler seed.

For correct and effective descrambling, the same scrambler is used for scrambling the transmitted data and descrambling the received data. When sending, the initial state of the scrambler is the scrambler seed defined by us. When receiving, the initial state of the descrambler at the receiving end should also be the scrambler seed defined by us. However, the receiving end does not know the scrambler seed, so it is impossible to set the initial state of the descrambler at the receiving end as the scrambler seed, so descrambling cannot recover the original data.

Therefore, in order to obtain the scrambling seed at the receiving end, before scrambling, the seven low significant bits of the SERVICE field are set to 0, so that when descrambling at the receiving end, the scrambled results of the seven zeros can be used as the initial state of the scrambling device at the receiving end, so as to carry out effective and correct descrambling.
3. Scrambling seed
When sending, the seven low significant bits of the SERVICE field have been set to 0, and the receiving end can deduce and calculate the scrambled results with the seven 0's to obtain the scramble seed, which is then used as the initial state of the scrambler at the receiving end. The scramble seed is solved as follows:
As shown in the figure:
Figure - structure of scrambler

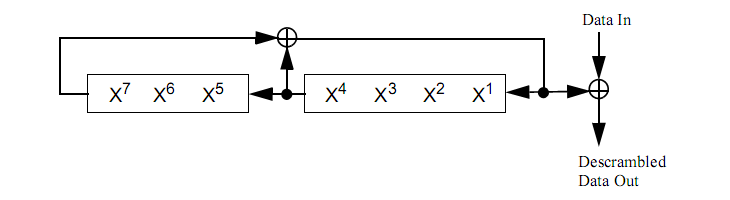
X1 – X7 is the initial state of the scrambler (scramble seed), and the input data is the seven zeros of the SERVICE field.
Output data (scrambled data):
S1 = X4 ⊕ X7；S2 = X3 ⊕ X6；S3 = X2 ⊕ X5；S4 = X1 ⊕ X4；
S5 = S1 ⊕ X3；S6 = S2 ⊕ X2；S7 = S3 ⊕ X1.
S1 – S7 are scrambled data, which can be directly received by the receiving end; Therefore, the expression of X1 – X7 can be obtained:
X1 = S1 ⊕ S5；X2 = S2 ⊕ S6；X3 = S3 ⊕ S7；X4 = X1 ⊕ S4；
X5 = X2 ⊕ S3；X6 = X3 ⊕ S2；X7 = X4 ⊕ S1.
Through the above expression, the scrambling code seed can be calculated at the receiving end, so as to correctly descramble the original data.

Scrambling and descrambling code

% Scrambling: note that when this function runs alone, the first seven digits should be all 0
function XL = raoma(input)
S = [1, 0, 0, 0, 0, 0, 0 ];%Initial state
L = zeros(1, 127);%127 Scrambling sequence
F= zeros(1, length(input));%Input data length
for i = 1:127
    A = S(1, 1);
    B = S(1, 4);
    C = xor(A, B);%XOR shift registers 4, 7
    S =[S(2:7),C];%    
    L(1,i) = C;%Scrambling sequence
end
L_copy = repmat(L, 1, ceil(length(input)/length(L)));
L_num = L_copy(1: length(input));%Match the length of the input data with the length of the scrambling code sequence
F= xor(L_num, input);
   
XL =  F;%Scrambled data sequence

Descrambling:
function XL=deraoma(output)
L = zeros(1, 127);%127 Descrambling sequence
F = zeros(1, length(output));%Output data length
s = output(1:7);
x1 = xor(s(1,3), s(1,7));
x2 = xor(s(1,2), s(1,6));
x3 = xor(s(1,1), s(1,5));
x4 = xor(x1,s(1,4));
S = [xor(x4,s(1,1)),xor(x3,s(1,2)),xor(x2, s(1,3)),x4,x3,x2,x1];
for i = 1:127
    t1 = S(1, 1); 
    t2 = S(1, 4);    
    t3 = xor(t1, t2);   
    S =[S(2:7),t3];   
    L(1,i) = t3; 
end
L_copy = repmat(L, 1, ceil(length(output)/length(L)));
L_num = L_copy(1: length(output));%Match the length of the input data with the length of the scrambling code sequence
F= xor(L_num, output);  
XL =  F;%Scrambled data sequence
 

Finally, thank you ~ ~ for your guidance.