Odd Palindrome

Question meaning: judge whether all substrings of a string are palindrome odd strings.
Idea: enumerate all substrings. If there is an even palindrome string, output no.

#include <iostream>
#include <cstring>
#include <algorithm>
using namespace std;
const int N = 1e5+10;
typedef long long LL;
int n,t,a[N];
string st;
bool check(int l,int r)
{
    for(int i=l,j=r;;i++,j--)
    {
        if(i==j||i>j) break;
        if(st[i]!=st[r]) return false;
    }
    return true;
}
int main()
{
    
    cin>>st;
    for(int i=0;i<st.size();i++)
    {
        for(int j=i;j<st.size();j++)
        {
            if(check(i,j))
            {  //cout<<i<<' '<<j<<endl;
               if(i-j+1%2==0)
               {
                   cout<<"Or not."<<endl;
                   return 0;
               }
            }
        }
    }
    cout<<"Odd."<<endl;
}

B - Latin Squares

Question meaning: judge that there are no duplicate elements in the row and column. Judge that the first row increases from left to right and the first column increases from top to bottom.
Idea: simulation

#include <iostream>
#include <algorithm>
#include <unordered_map>
#include <vector>
typedef long long LL;
using namespace std;
int g[40][40];
LL n;
int check(int l,int r)
{
  //  cout<<g[l][r]<<endl;
  //  cout<<n<<endl;
    for(int i=1;i<=n;i++)
    {   //cout<<g[1][1]<<"!!!";
        if(g[l][r]==g[l][i]&&i!=r) return 0;
    }
       
    for(int i=1;i<=n;i++)
    {
        if(g[l][r]==g[i][r]&&i!=l) return 0;
    }
       
  //  cout<<l<<"  !  "<<r<<endl;
    return 1;
}
int main()
{
    while(cin>>n)
    {
        for(int i=1;i<=n;i++)
        {
            getchar();
            for(int j=1;j<=n;j++)
            {
                char ss;
                cin>>ss;
                if(ss>='A'&&ss<='Z')
                {
                    g[i][j]=int(ss-'A'+10);
                }
                else
                {
                    g[i][j]=ss-'0';
                }
            }
        }
       /* for(int i=1;i<=n;i++) 
           {
             for(int j=1;j<=n;j++)
           {
               cout<<g[i][j];
           }
           cout<<endl;
               
           }*/
        int flag=1;
        for(int i=1;i<=n;i++)
        {
            for(int j=1;j<=n;j++)
            {
                if(!check(i,j))
                {
                    flag=0;
                }
            }
        }
        if(flag==0)
        {
            cout<<"No"<<endl;
            continue;
        }
        else
        {
            for(int i=2;i<=n;i++)
            {
                if(g[1][i]!=g[1][i-1]+1)
                {
                    flag=2;
                   // cout<<i<<' '<<'!';
                    break;
                }
            }
            for(int i=2;i<=n;i++)
            {
                if(g[i][1]!=g[i-1][1]+1)
                {
                    //cout<<i<<' '<<'!';
                    flag=2;
                    break;
                }
            }
            if(flag==1)
            {
                cout<<"Reduced"<<endl;
            }
            else if(flag==2)
            {
                cout<<"Not Reduced"<<endl;
            }
        }
    }
    
}

C - Fear Factoring

Meaning:
Find the sum of all factors of each number in 1-n, and add these factor sums.
For example, the factor of 1 - 3: 1 has 1, the factor of 2 has 1 + 2 = 3, and the factor of 3 has 1 + 3 = 4. The final answer is 1 + 3 + 4 = 8.
Source of supplementary questions
The time complexity problem is solved by dividing blocks and summing equal difference sequences.
n i by 1 reach n in each one individual about number i Out present of total second number \frac{n}{i} is the total number of occurrences of each divisor i from 1 to n In is the total number of occurrences of each divisor i in 1 to n

However, direct enumeration takes a lot of time. Here, the arithmetic sequence is used to enumerate blocks.
The left interval is the previous right interval + 1 every time.
Right interval, for example 10 / 6 = 1 , 10 / 10 = 1 10/6=1,10/10=1 10 / 6 = 1,10 / 10 = 1. For those intervals with divisor 1, we use 10 / 1 = 10 10/1=10 If 10 / 1 = 10, you can directly get the endpoint of the right section. See the blogger's notes for details.

#include <iostream>
#include <cstdio>
#include <algorithm>
/*
    Here we subtract the sum of the divisors between 1 ~ a - 1 from the sum of the divisors between 1~b
    Therefore, the answer may explode long long when seeking, which is defined as unsigned long long here 
    */
typedef unsigned long long ll;
using namespace std;

ll sum(ll n)
{
    ll ans = 0;
    for(ll left = 1, right; left <= n; left = right + 1 )
    {
        right = n/(n/left);
        // (left + right) * (right - left + 1) / 2 is the sum of the arithmetic sequence
        ans += (left + right) * (right - left + 1) / 2 * (n/left);
    }
    return ans;
}

int main(void)
{
    ll a, b;
    while(cin >> a >> b)
    {
        cout << sum(b) - sum(a - 1) << endl;
    }
    return 0;
}

Halfway

Given a number n, the completion of a project is C n 2 C_n{2} Cn ＾ 2 enumerates a sequence from 1 to N. from the front to the back, ask to enumerate to the closing time, the project has completed the general times, and the left interval is output.
Idea: direct simulation, first find out the total number of times, and then decrease from n by the arithmetic sequence.

#include <iostream>
#include <cstring>
#include <algorithm>
#include <cmath>
using namespace std;
const int N = 1e5+10;
typedef long long LL;
LL n,m,k,p,x,a[N];
string st;
int main()
{
    cin>>n;
    LL res=0,ans;
    res=n*(n-1);
    res/=2;
    if(res%2==0) ans=res/2;
    else ans=res/2+1;
    for(int i=1;i<=n;i++)
    {
        ans-=n-i;
        if(ans<=0)
        {
            cout<<i<<endl;
            return 0;
        }
    }
}

Unloaded Die

Meaning: the score of a six sided sieve is expected to be 3.5, and the probability of each face is one sixth. Given the special probability of six faces, if the expectation of this sieve is consistent with that of normal dice by modifying the face value of one face, and the face value to be changed can be as small as possible, find the difference between the absolute value of the face value to be changed.
Idea: find the minimum change △ x △x △ x, first calculate the current expectation and make a difference from 3.5—— △ y △y △ y, then calculate the maximum probability given by the topic p p p. Minimum change △ x = △x= △x= △ y p \dfrac{△y}{p} p △ y, the greedy point is that if the face value you want to change is small, you can add the value to the side with high probability.

#include <iostream>
#include <algorithm>
#include <unordered_map>
#include <vector>

using namespace std;
double s[10];
typedef long long LL;
int main()
{
    double a,b,c,d,e,f;
    double mx=0;
    cin>>s[1]>>s[2]>>s[3]>>s[4]>>s[5]>>s[6];
    double ans=0;
    for(int i=1;i<=6;i++)
    {
        mx=max(mx,s[i]);
        ans+=i*s[i];
    }
    double xx=abs(3.5-ans);
    double y=xx/mx;
    printf("%.3lf\n",y);
    
}

Star Arrangements

When simulating and enumerating, we should pay attention to the adjacent solutions of the topic description. My practice is more violent.

#include <iostream>
#include <algorithm>
#include <unordered_map>
#include <vector>
typedef long long LL;
using namespace std;
double s[10];
LL n;

bool check1(int l,int r)
{
    for(int i=1;;i++)
    {
        if((i+1)*l+(i)*r==n) return true;
        if((i+1)*l+(i)*r>n) return false;
    }
}
bool check2(int l,int r)
{
    for(int i=1;;i++)
    {
        if(i*l+(i)*r==n) return true;
        if(i*l+(i)*r>n) return false;
    }
}
int main()
{
    cin>>n;
    cout<<n<<":"<<endl;
    for(int i=2;i<n;i++)
    {
        if(check1(i,i-1)||check2(i,i-1)) cout<<i<<','<<i-1<<endl;
        if(check2(i,i)||check1(i,i)) cout<<i<<','<<i<<endl;
    }
}

L - Delayed Work

Given k,p,x. Each worker can work k days, pay a fine of p every day, and pay a rent of x. The actual number of days required is k m \dfrac{k}{m} mk and m are the number of people to rent. This number can be any value. You can select the number of people to rent to minimize the cost.
Idea: suppose the number of people renting is n n n, cost c o s t = cost= cost= n ⋅ x + k n ⋅ p n·x+\dfrac{k}{n}·p n ⋅ x+nk ⋅ p, when n = n= n= k ⋅ p x \sqrt{\dfrac{k·p}{x}} xk⋅p​ The minimum value is obtained when 2 x ⋅ k ⋅ p 2\sqrt{x·k·p} 2x⋅k⋅p ​.

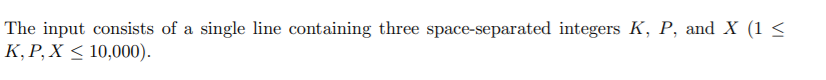
As can be seen from the scope of the question n = n= n= k ⋅ p x \sqrt{\dfrac{k·p}{x}} xk⋅p​ , the worst k and p are max and x is 1 At this time, n=1e5. Therefore, you can enumerate the first 1e5 data and update the minimum value. Of course, because it is known that n takes the minimum value at this point, you can only enumerate n , n − 1 , n + 1 n,n-1,n+1 n. Find the minimum value at the three points of n − 1 and N + 1.

Forbidden Zero

Given a number n, let you find the next number that increases in dictionary order and does not contain 0. as 9 − − − − 11 9----11 9−−−−11
Idea: find a continuous one from right to left 9 9 The number of 9, and then find the sum of the numbers to the tenth power. such as 1199 1199 1199, two 9 9 9, and is 1 0 2 + 1 0 1 + 1 0 0 = 12 10^2+10^1+10^0=12 102 + 101 + 100 = 12, so the answer is 1211 1211 1211.

#include <iostream>
#include <cstring>
#include <algorithm>
#include <cmath>
using namespace std;
const int N = 1e5+10;
typedef long long LL;
int n,t,a[N];
string st;

int main()
{
    cin>>n;
    LL m=n,res=0,ans=0;
    LL p=n,ct=0;
    while(p)
    {
        int x=p%10;
        if(x!=9) break;
        p/=10;
        if(x==9) ct++;
    }
    for(int i=ct-1;i>=0;i--)
    {
        ans+=pow(10,i);
    }
     if(n%10==9)
     cout<<n+ans+1;
     else
     cout<<n+1;
}