A - Amanda Lounges

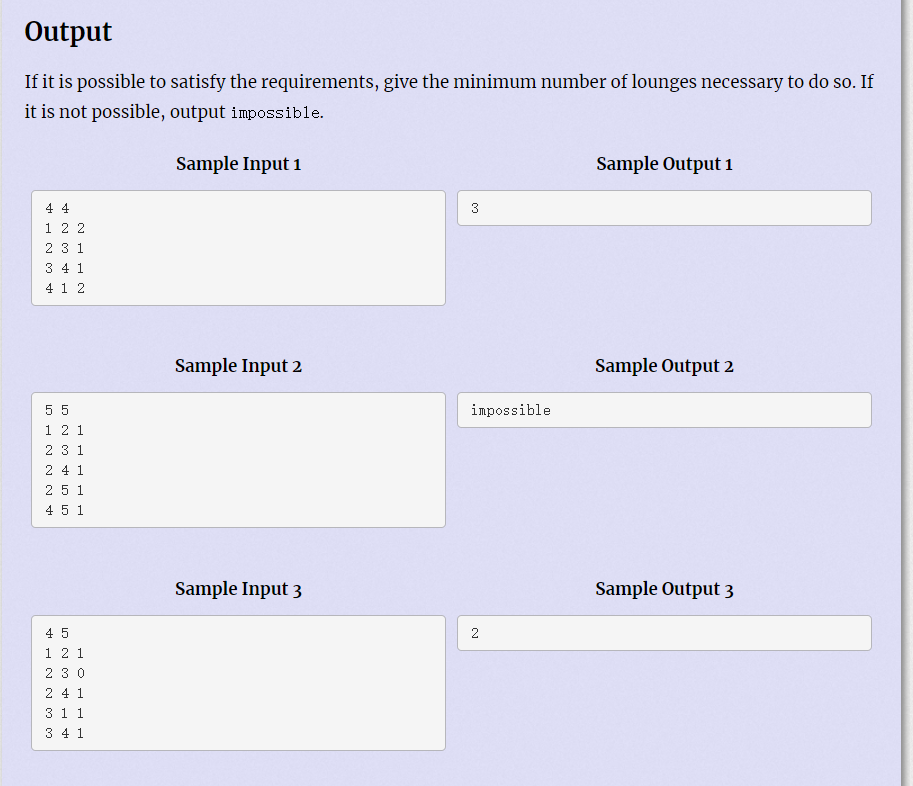
Question meaning: there are n airports and m routes (the route is the side connecting two airports). For each airport, a waiting room may or may not be required. If you enter 2, both airports connected by the route need to be established, enter 1, one airport connected by the route is established (required), and enter 0, both airports connected by the route cannot be established, How many waiting rooms should you set up at least
Idea: staining + DFS
The airport is the point of graph theory
For input 2, the input two-point color is marked as' 1 '
When inputting 1, the input two-point color can be marked as' - 1 '
For the above two cases, if there is a contradiction during dyeing, it is directly "impossible"
When entering 1, the two points entered are temporarily marked as' 0 ', representing the color to be determined
And only for the two points input when 1 is input (to facilitate the following dfs search)
Then, after the edge is created, multiple closed graphs will appear, and there will be many cases of points in them.
At this time, the graph is classified into two categories: all points in the graph are 0 and some points in the graph are not 0
First search the graph with points other than 0, because the established edges are established by inputting 1, so when the color of one point is known, the color of all other points in the closed graph can be deduced For example, if a point is - 1, the points connected to this point should be 1, because the connected point can only have one waiting room. A point is 1, and the points connected to this point should be - 1. The principle is as follows.
In the process of search + dyeing, if the color of a point is consistent with that of the connected points, it indicates a contradiction and exits directly
Then dye the graph with all zeros. At this time, you need to set a color for a point of the graph, either set to 1 or - 1. Search for + coloring in both cases, Finally, take the minimum value dyed to 1 (in fact, do not search twice with code. The number of 0 and 1 finally formed by dyeing to 0 and dyeing to 1 must be relative. If you know one, you will know the other, so take the minimum value directly)
(it's a good question of dyeing + DFS, which tests the code ability)

#include <bits/stdc++.h>
using namespace std;
int n, m;
const int N = 4e5 + 10;
int e[N], ne[N], h[N], idx;
int color[N];
int vis[N];
int a, b, res;
void add(int a, int b) { e[idx] = b, ne[idx] = h[a], h[a] = idx++; }
int dfs(int u, int c, int k) {
    if (k) {
        if (color[u] == 1) {
            b++;
        } else
            a++;
    } else {
        if (color[u] == 1) res++;
    }
    for (int i = h[u]; i != -1; i = ne[i]) {
        int j = e[i];
        if (color[j] == c) return 0;
        if (vis[j] == 0) {
            vis[j] = 1;
            if (color[j] == 0) {
                color[j] -= c;
            }
            if (!dfs(j, color[j], k)) {
                return 0;
            }
        }
    }
    return 1;
}
int main() {
    memset(h, -1, sizeof(h));
    cin >> n >> m;
    int flag = 1;
    //012 classified dyeing edge construction
    for (int i = 0; i < m; i++) {
        int x, y, z;
        scanf("%d%d%d", &x, &y, &z);
        if (z == 2) {
            if (color[x] == -1 || color[y] == -1) {
                flag = 0;
            }
            color[x] = 1, color[y] = 1;
        } else if (z == 0) {
            if (color[x] == 1 || color[y] == 1) {
                flag = 0;
            }
            color[x] = -1, color[y] = -1;
        } else {
            add(x, y), add(y, x);
        }
    }
    //Diffusion coloring is performed on graphs with 1 or - 1 points
    for (int i = 1; i <= n; i++) {
        if (!vis[i] && color[i]) {
            vis[i] = 1;
            if (dfs(i, color[i], 0) == 0) {
                flag = 0;
            }
        }
    }
    //For a graph with only 0, select a point and set it to 1, and then diffuse coloring
    for (int i = 1; i <= n; i++) {
        if (vis[i] == 1) {
            continue;
        }
        a = 0, b = 0, vis[i] = 1, color[i] = 1;
        if (dfs(i, 1, 1) == 0) {
            flag = 0;
        }
        res += min(a, b);
    }
    if (flag)
        printf("%d\n", res);
    else
        puts("impossible");
    return 0;
}

E - Opening Ceremony

There are two operations for n high-rise buildings. Either select a number, and all high-rise buildings with a height lower than this number will be reduced by one floor. Or directly destroy a tall building and ask how many operations at least make all tall buildings destroyed
Idea: at the beginning, I thought of cutting floors one by one, looking at the horizontal cutting once, and then I need to cut down several tall buildings vertically until it is finished. Finally, I can take the minimum value in all cases. Then I found that when cutting horizontally, the smallest falling building must be the shortest, followed by the second lowest, and go down in turn. Then you can make a decision. From the front to the back, select a building. Cut all the buildings shorter than this building horizontally (the number of horizontal cuts is the height of the selected building) + the number of tall buildings to be cut vertically behind. Finally, calculate them all and take the minimum value.

#include <bits/stdc++.h>
using namespace std;
const int N = 100010;

int a[N];
int main() {
    int n;
    cin >> n;
    int res = n;
    for (int i = 0; i < n; i++) {
        scanf("%d", &a[i]);
    }
    sort(a, a + n);
    res = min({n, a[n - 1]});
    for (int i = 1; i <= n; i++) {
        res = min(res, n - i + a[i - 1]);
    }
    cout << res << endl;
}

To be continued
If you have any suggestions or criticisms and additions, please leave a message and point it out. Thank you very much