① Linear lookup:
1) The simplest search algorithm: directly scan the array with the for loop, look at each number, find the desired number, or count the desired results;

//Find how many numbers are equal to x
for (int i=0;i<n;i++){
	if(a[i]==x){
		cnt++;
	}
}

//Find the first position equal to x
int p=-1;//Nonexistence is represented by - 1
for(int i=0;i<n;i++){
	if(a[i]==x){
		p=i;
		break;//Find it and jump out in time. Don't let the program continue to find it
	}
}

Example 1: find the number that meets the requirements
Title: find and count how many numbers are greater than or equal to l and less than or equal to r.
Idea:
Look at each bit of the array with the for loop;
Full code:

#include <iostream>
using namespace std;
int a[1005];
int main() {
    int n, l, r, cnt = 0;
    cin >> n >> l >> r;
    for (int i = 0; i < n; i++) {
        cin >> a[i];
    }
    for(int i=0;i<n;i++){
        if(a[i]>=l&&a[i]<=r){
            cnt++;
        }
    }
    cout << cnt << endl;
    return 0;
}

② Binary Search:
1) It is an efficient search method;
2) Algorithm requirements:
<1> Sequential storage structure must be adopted (random access is supported), such as array and vector;
<2> It must be sorted in order by keyword size (that is, find a keyword for the elements in an ordered array);
3) Algorithm steps:

Tips:
1) In C + +, there is a built-in binary lookup function - binary in the header file_ search；

//Indicates the search keyword 1 from a[0] to a[6]
//Similar to sort function
binary_search(a,a+7,1);

Tips: 1) before binary search, it is necessary to ensure that the parts to be searched are sorted from small to large. That is, generally, the entire array is sorted from small to large. 2) Duplicate elements in the array do not affect the search. That is, there can be repeated elements;
3) The return value of the function is bool type. When true is returned, it means that the value is found in the array; otherwise, it means that the value is not found;
4) In the dynamic array vector, use * *. Begin() and. End() * *, that is, binary_search(a.begin(),a.end(),x) or binary_search(a.begin()+l,a.begin()+r,x);

PS: two supplementary functions

Summary:
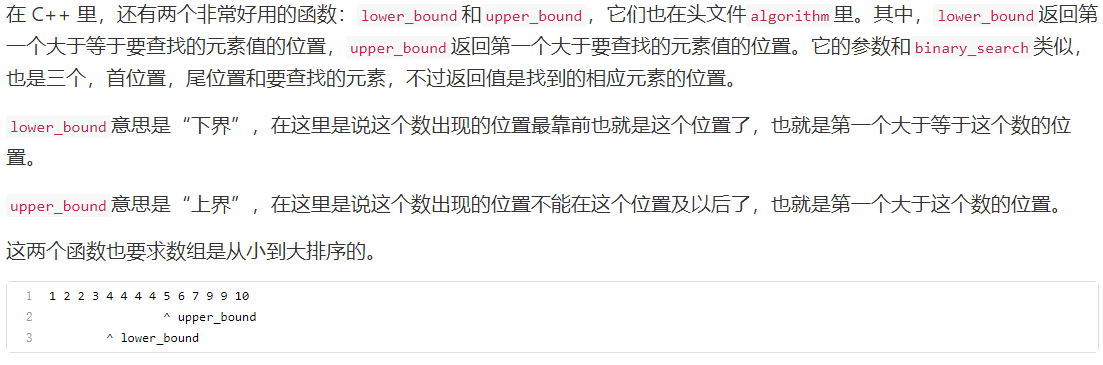
eg: find the number 4
1.binary_search(a,a+7,4) find '4' - > bool
2. lower_bound(a,a+7,4) find the first position greater than or equal to '4' - > position
(to get the subscript of the array, lower_bound(a,a+7,4)-a)
3.lower_bound(a,a+7,4) find the first position greater than '4' - > position
(to get the array subscript, lower_bound(a,a+7,4)-a)
4. There is an array a with subscripts 0 to n-1 arranged from small to large. If you want to know the number of elements x, you can use upper_bound(a,a+n,x)-lower_bound(a,a+n,x)；
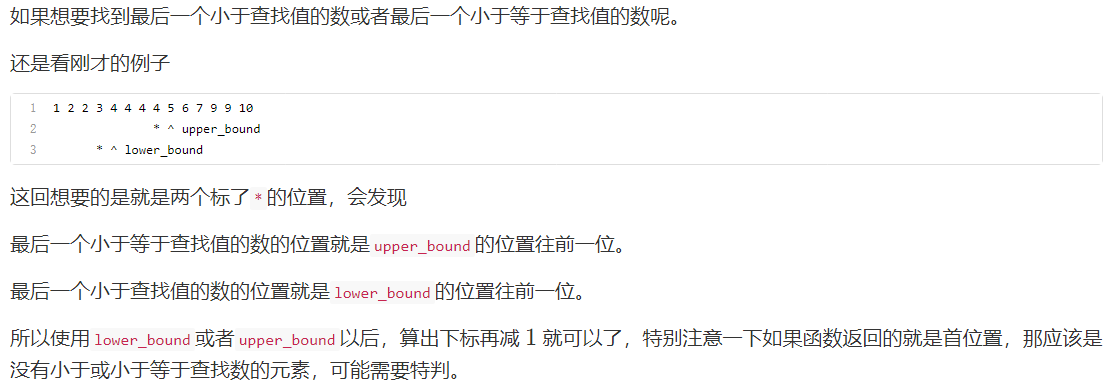
5. There are also two special cases:
be careful:
Using binary_search,lower_bound,upper_ When using the bound function, the part of the array to be searched must be sorted from small to small;

Example 2: sum is a given number



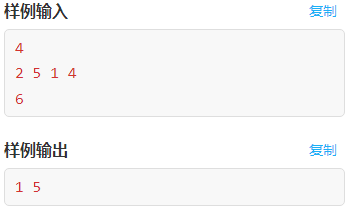
Complete code

#include <cstdio>
#include <iostream>
#include <algorithm>
using namespace std;
int num[100005];
int main() {
    freopen("sum.in", "r", stdin);
    freopen("sum.out", "w", stdout);
    int n, m;
    bool f = false;
    cin >> n;
    for (int i = 0; i < n; i++) {
        cin >> num[i];
    }
    cin >> m;
    // Please fill in the appropriate code here
    sort(num,num+n);//Avoid duplicate lookups, like a double-layer loop with forj=i
    for (int i = 0; i < n; i++) {
        if (binary_search(num+i+1,num+n,m-num[i])) { // Please fill in the conditions here
            cout << num[i] << " " << m - num[i] << endl;
            f = true;
            break;
        }
    }
    if (!f) {
        cout << "No" << endl;
    }
    return 0;
}

Tips:
1) Set a flag f and initialize it to false. If the conditions are met, it is overwritten with true assignment;
Example 3: find the closest element



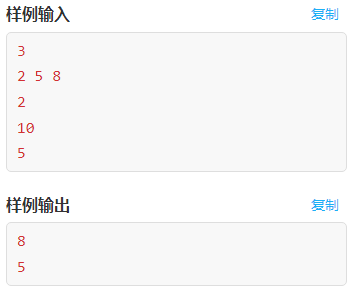
Complete code

#include <cstdio>
#include <iostream>
#include <algorithm>
using namespace std;
int num[100005];
int main() {
    freopen("closest.in", "r", stdin);
    freopen("closest.out", "w", stdout);
    int n, m, x;
    cin >> n;
    for (int i = 0; i < n; i++) {
        cin >> num[i];
    }
    cin >> m;
    while (m--) {
        cin >> x;
        long long p1, p2, ans1, ans2;
        ans1 = ans2 = 0x3f3f3f3f;//Infinite constant
        p1 = lower_bound(num, num + n , x) - num;//Is greater than or equal to the smallest decimal of the number to be checked
        p2 = p1 - 1;//Less than the maximum number to be checked
        if (p1 != n) {
        ans1 = num[p1] - x;
        }
        if (p2 != -1) {
            ans2 = x - num[p2];
        }
        if (ans1 < ans2) {//p2=-1
            cout << num[p1] << endl;
        } else {                     //p1=n，
            cout << num[p2] << endl;
        }
    }
    return 0;
}

Tips: 0x3f3f3f3f -- infinity constant in ACM 1) in algorithm competitions, we often need to set a constant to represent "infinity".

1. For example, for int type numbers, some people will use INT_MAX, that is 0x7fffff as infinity. But with INT_MAX for infinity often faces a problem, that is, adding another number will overflow. This situation often occurs in dynamic programming or other recursive algorithms, which is likely to lead to problems in the algorithm.
2. Therefore, in the algorithm competition, we often use 0x3f3f3f3f as infinity. 0x3f3f3f3f3f mainly has the following advantages: 1 > the decimal system of 0x3f3f3f is 1061109567, and INT_MAX is an order of magnitude, i.e. 109. In general, the data is less than 109.
   2> 0x3f3f3f3f3f * 2 = 2122219134, the addition of infinity will not overflow. You can use memset (array, 0x3f, 3 > sizeof (array)) to set the initial value of the array to 0x3f3f3f, because each byte of this number is 0x3f.