Sequential search algorithm

Sequential search, also known as linear search, is the most basic search technology. Its search process is: start from the first (or last) record in the table, compare the keyword of the record with the given value one by one. If the keyword of a record is equal to the given value, the search is successful and the searched record is found; If the keyword and given value of the last (or first) record are not equal until the comparison, there is no queried record in the table and the search is unsuccessful.

code:

int Sequential_Search(int*a,int n,int key)
{
    int i;
    for(i=1;i<=n;i++)
    {
        if(a[i]==key)
        return i;
    }
    return 0;
}

Code optimization:

int Sequential_Searchval(int*a,int n,int key)
{
    int i;
    a[0]=key;
    i=n;
    while(a[i]!=key)
    {
        i--;
    }
    return i;
}

Complexity analysis:

The average search length when the search is successful is: (assuming that the probability of each data element is equal)
　　 ASL = (1+2+3+...+n)/n = (n+1)/2 ;
When the search is unsuccessful, n+1 comparisons are required, and the time complexity is O(n);
Therefore, the time complexity of sequential search is O(n).

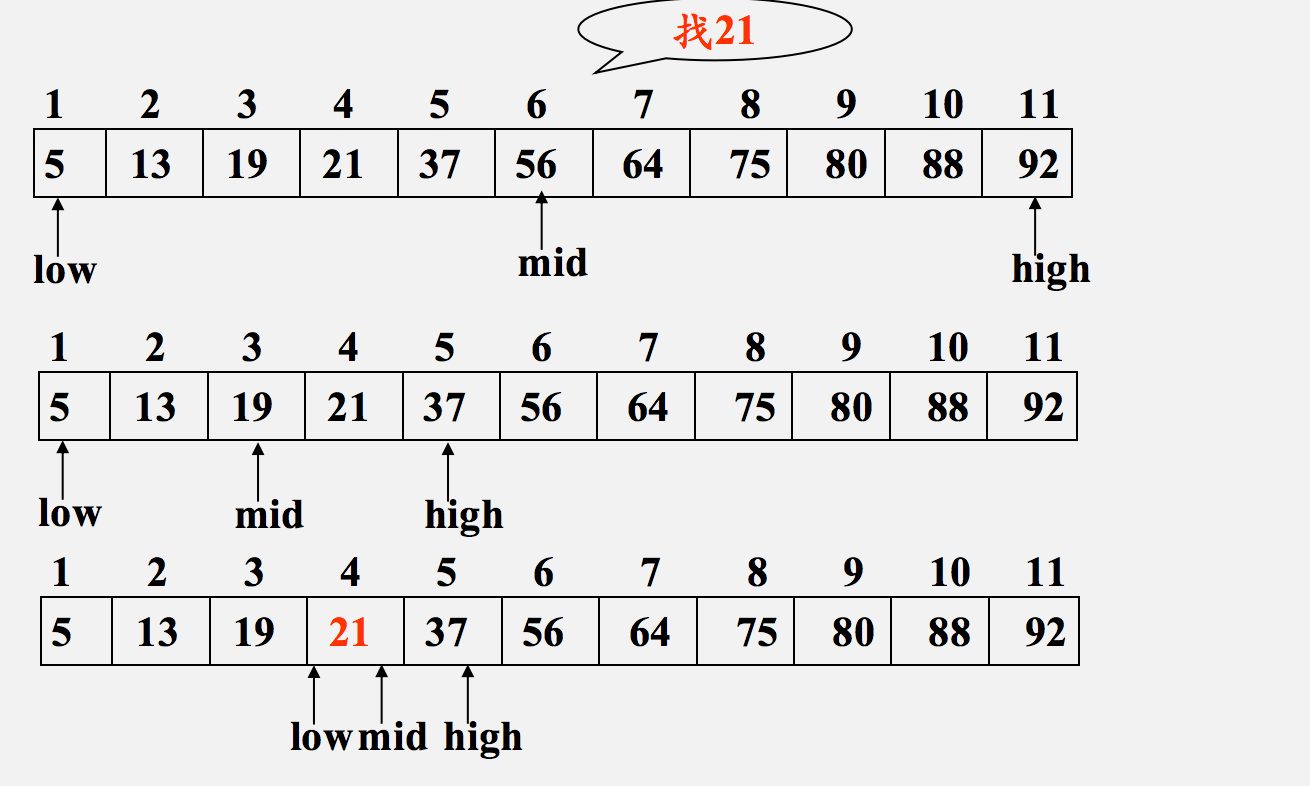
Half search algorithm

The core of half search, also known as binary search, is to find key s by constantly narrowing the scope of filtering.
Taking the ascending sequence as an example, compare the size of an element with the element in the middle of the sequence. If it is larger than the element in the middle, continue to search in the sequence in the second half; If it is smaller than the element in the middle position, it is compared in the first half of the sequence; If equal, the position of the element is found. The length of each comparison sequence will be half of the previous sequence until the position of the equal element is found or the element to be found is not found.
This is the simple idea of binary search

code implementation

int Binary_Search(int*a,int n,int key)
{
    int low,high,mid;
    low=1;
    high=n;
    while(low<=high)
    {
        mid=(low+high)/2;
        if(a[mid]>key)
        {
            high=mid-1;
        }
        else if(a[mid]<key)
        {
            low=mid+1;
        }
        else
        return mid;
    }
    return 0;
}

Interpolation search algorithm

In the previous binary search, mid=(1/2)*(low+high)

This formula can be reduced to mid = (low + high) / 2 = Low + (1 / 2) * (high low)

Now, let's improve the previous coefficient (high low)

Change to (key-A [low] / (a [high] - a [low]). Why? If you think carefully, you will find that this calculation will make the mid value closer to the subscript of the target value key. In this way, you can further optimize the search process based on the binary search algorithm

Interpolation search is a search method based on the comparison between the keyword Key to be searched and the keyword of the largest and smallest record in the lookup table. Its core is the difference calculation formula (key-a[low])/(a[high]-a[low])

Code implementation:

int Interpolation_Search(int*a,int n,int key)
{
    int low,high,mid;
    low=1;
    high=n;
    while(low<=high)
    {
        mid=low+(key-a[low])/(a[high]-a[low])*(high-low);
        if(key>a[mid])
        {
            low=mid+1;
        }
        else if(key<a[mid])
        {
            high=mid-1;
        }
        else
        return mid;
    }
    return 0;
}

fibonacci search

Implementation premise: there is a set of Fibonacci arrays
Fibonacci search principle: similar to the first two, it only changes the position of the intermediate node (MID), and the mid is no longer obtained by intermediate or interpolation
It is located near the golden section, that is, mid=low+F(k-1)-1
deduction:
From the properties of Fibonacci sequence, we get F[k]=F[k-1]+F[k-2], and then we can get it,
(F[k]-1)=(F[k-1]-1)+(F[k-2]-1)+1;
The above formula is well derived
Combined with the following figure, it can be deduced that when mid=low+F(k-1)-1, mid is at the golden section point

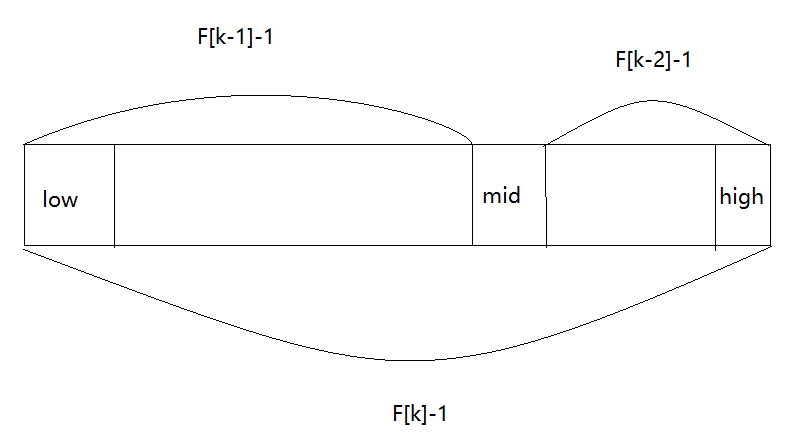
However, the length n of the sequence table is not necessarily equal to F[k]-1, so it is necessary to increase the length n of the original sequence table to F[k]-1, as long as K can make
F[k]-1 is exactly greater than or equal to n.
Namely:

 while(n>F[k]-1)
        k++;

Code implementation:

int Fib_Search(int*a,int n,int key)
{
    int low,high,mid,i,k;
    low=1;
    high=n;
    k=0;
    while(n>F[k]-1)
        k++;
    for(i=n;i<F[k]-1;i++)
        a[i]=a[n];      //Complete the dissatisfied values and fill them according to the last element of the array
    while(low<=high)
    {
        mid=low+F[k-1]-1;
        if(key<a[mid]) //Find in front of array
        {
            high=mid-1;
            k=k-1;
           		  //1. All elements = front elements + rear elements
                  //2. There are F[k-1] front elements, F[k] = F[k-1] + F[k-2]
                  //3.F[k-1] = F[k-2] + F[k-3]
                  //That is, continue searching in front of F[k-1]
                  //So k=k-1
        }
        else if(key>a[mid])  //Find after array
        {
            low=mid+1;
            k=k-2;
                  //1. All elements = front elements + rear elements
                  //2.F[k] = F[k-1] + F[k-2]
                  //3. There are F[k-2] following elements, F[k-2]=F[k-3] + F[k-4]
                  //That is, continue to search after F[k-2]
                  //So k=k-2
        }
        else
        {
            if(mid<=n)
                 return mid;
            else
                return n;
        }
    }
    return 0;

}