Characteristics of array
- The biggest advantage of arrays is that they can be queried quickly, because arrays can be queried quickly directly through the index: array[2], so they have certain advantages in random access. Its data structure is a simple linear sequence, which makes element access very fast and it is convenient to traverse the array according to the index.
- Arrays are best used when the index has meaning
- But not all semantic indexes are applicable to arrays, such as index numbers of the ID number, which can not be used as index.
- The array can also handle the case of "index has no semantics"
- Disadvantages of arrays:
– slow to find elements based on content
– once the size of the array is determined, it cannot be changed
- an array can store only one type of data
– low efficiency of inserting, specifying and deleting elements
– no method is encapsulated, and all operations need to be defined by the user
Secondary encapsulation of podium array
Problems encountered in the case of "index has no meaning" based on the appeal:
- If the index has no semantics, how does it mean that there are no elements?
- How to add elements? How to delete an element? How to modify elements?
So we want to encapsulate the array in Java into our own array container to solve these problems.
Main frame
We encapsulate it in a class named Array. First, write the basic framework of the Array class:
public class Array {
/**
* Array of actual data
*/
private int[] data;
/**
* Represents the number of elements in the array
*/
private int size;
/**
* The capacity of the passed in Array is used to construct the Array
* So that users can customize the capacity of the array
*
* @param capacity capacity
*/
public Array(int capacity) {
data = new int[capacity];
size = 0;
}
public Array() {
// The default array capacity is 10
this(10);
}
/**
* Gets the number of elements in the array
*
* @return Number of elements in the array
*/
public int getSize() {
return size;
}
/**
* Gets the capacity of the array
*
* @return Capacity of the array
*/
public int getCapacity() {
return data.length;
}
/**
* Returns whether the array is empty
*
* @return If it is empty, return true; otherwise, return false
*/
public boolean isEmpty() {
return size == 0;
}
@Override
public String toString() {
if (isEmpty()) {
return "[]";
}
StringBuilder sb = new StringBuilder();
sb.append(String.format("Array: size = %d, capacity = %d\n", size, data.length));
sb.append("[");
for (int i = 0; i < size; i++) {
sb.append(data[i]);
if (i != size - 1) {
sb.append(", ");
}
}
return sb.append("]").toString();
}
}
Adding elements to an array
After the main framework is written, you need to add elements to the array. The simplest way is to add elements to the end of the array, because size always points to the position of the last element + 1, that is, the first position without elements at the end of the array. Therefore, when adding elements, we can place the elements in the position of size, and then we need to maintain size and make it + 1, so that size continues to point to the end of the array, and so on.
/**
* Adds a new element to the position of the last element + 1
*
* @param e New element
*/
public void addLast(int e) {
// If the array is full, an exception will be thrown. Dynamic capacity expansion will not be performed here for the time being
if (size == data.length) {
throw new IllegalArgumentException("AddLast failed. Array is full.");
}
data[size] = e;
size++;
}
However, under some special requirements, it may be necessary to add elements to the specified position. For example, the elements in the array are orderly. I want to insert the new elements into the appropriate position to ensure the ordering of the elements in the array, as shown in the following figure:
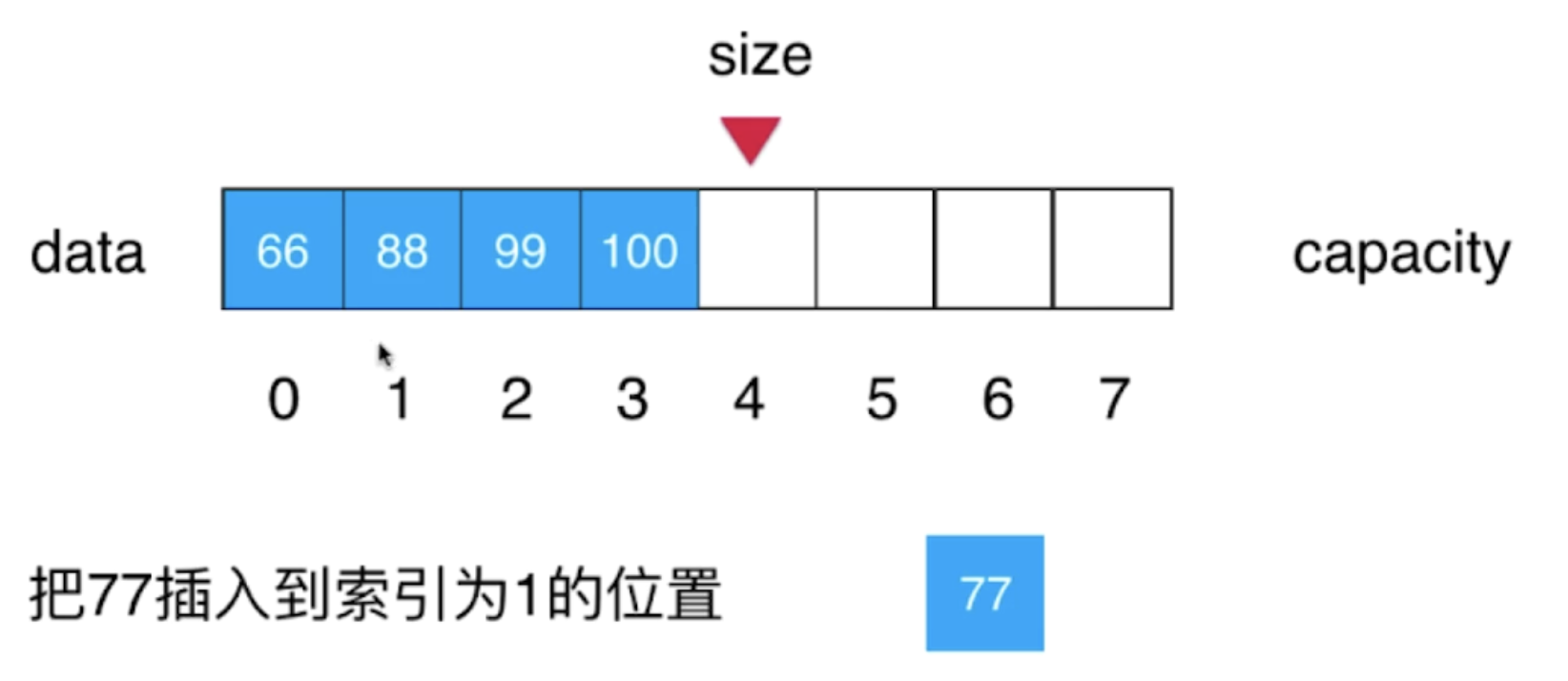
/**
* Insert a new element e under the index position
*
* @param index Indexes
* @param e New element
*/
public void add(int index, int e) {
if (size == data.length) {
throw new IllegalArgumentException("Add failed. Array is full.");
}
// If the index is negative or the index is greater than size, an exception is thrown
// Because if the index is greater than size, the elements in the array will not have continuity, and if the index is less than 0, it is an invalid index
if (index < 0 || index > size) {
throw new IllegalArgumentException("Add failed. Require index >= 0 and index <= size.");
}
// The elements in the array are traversed from the last element until the index position pointed to by the index is reached
for (int i = size - 1; i >= index; i--) {
// Move each element back one bit
data[i + 1] = data[i];
}
// You can also directly use the function of array copy to implement this logic. Here, in order to indicate the logic of insertion, array copy is not used
// System.arraycopy(data, index, data, index + 1, size - index);
// Insert a new element at the index position
data[index] = e;
// Last size needs + 1
size++;
}
After the method of inserting at the specified location is implemented, we can reuse the method and simplify the previous addLast as follows:
/**
* Adds a new element to the position of the last element + 1
*
* @param e New element
*/
public void addLast(int e) {
add(size, e);
}
Similarly, this method can be reused to add a new element to the front of the array, as follows:
/**
* Add a new element before all elements
*
* @param e New element
*/
public void addFirst(int e) {
add(0, e);
}
Query and modify elements in an array
We often need to query specific elements and modify specific elements. The implementation of these two logics is also very simple. When users modify and query specific elements, they need to pass in the index, so before that, we will encapsulate a private method to check whether the index is legal, so that other methods can reuse this logic without repeatedly writing the logic to check the index.
/**
* Check whether the index is legal
*
* @param index index
*/
private void checkIndex(int index) {
// If the index is negative or the index is greater than or equal to size, an exception is thrown
// Because when the index is greater than or equal to size, users will access invalid data, and when the index is less than 0, it is an invalid index
if (index < 0 || index >= size) {
throw new IllegalArgumentException("Require index >= 0 and index <= size.");
}
}
Then implement the method of querying specific elements and modifying specific elements:
/**
* Gets the element at the index position
*
* @param index index
* @return index Element at index position
*/
public int get(int index) {
checkIndex(index);
return data[index];
}
/**
* Gets the last element in the array
*
* @return Last element
*/
public int getLast() {
return get(size - 1);
}
/**
* Gets the first element in the array
*
* @return First element
*/
public int getFirst() {
return get(0);
}
/**
* Modify the element of index position to e
*
* @param index index
* @param e e
*/
public void set(int index, int e) {
checkIndex(index);
data[index] = e;
}
Include, search, and delete
When there are a certain number of elements in our array, we often encounter a requirement to query whether these elements contain a specific element. Another common requirement is to query the index position of a specific element, that is, search the element and return the index of the element. If the element does not exist, it will return a specific value, generally - 1, because - 1 usually represents an invalid index.
/**
* Find whether there is an element e in the array
*
* @param e e
* @return true is returned, false is not returned
*/
public boolean contains(int e) {
int index = indexOf(e);
return index != -1;
}
/**
* Find the index of element e in the array. If element e does not exist, return - 1
*
* @param e e
* @return Index of element e, or - 1
*/
public int indexOf(int e) {
for (int i = 0; i < size; i++) {
if (data[i] == e) {
return i;
}
}
return -1;
}
Next, let's see how to delete the element with the specified index position. For example, I want to delete the element with index 1, as shown in the following figure:
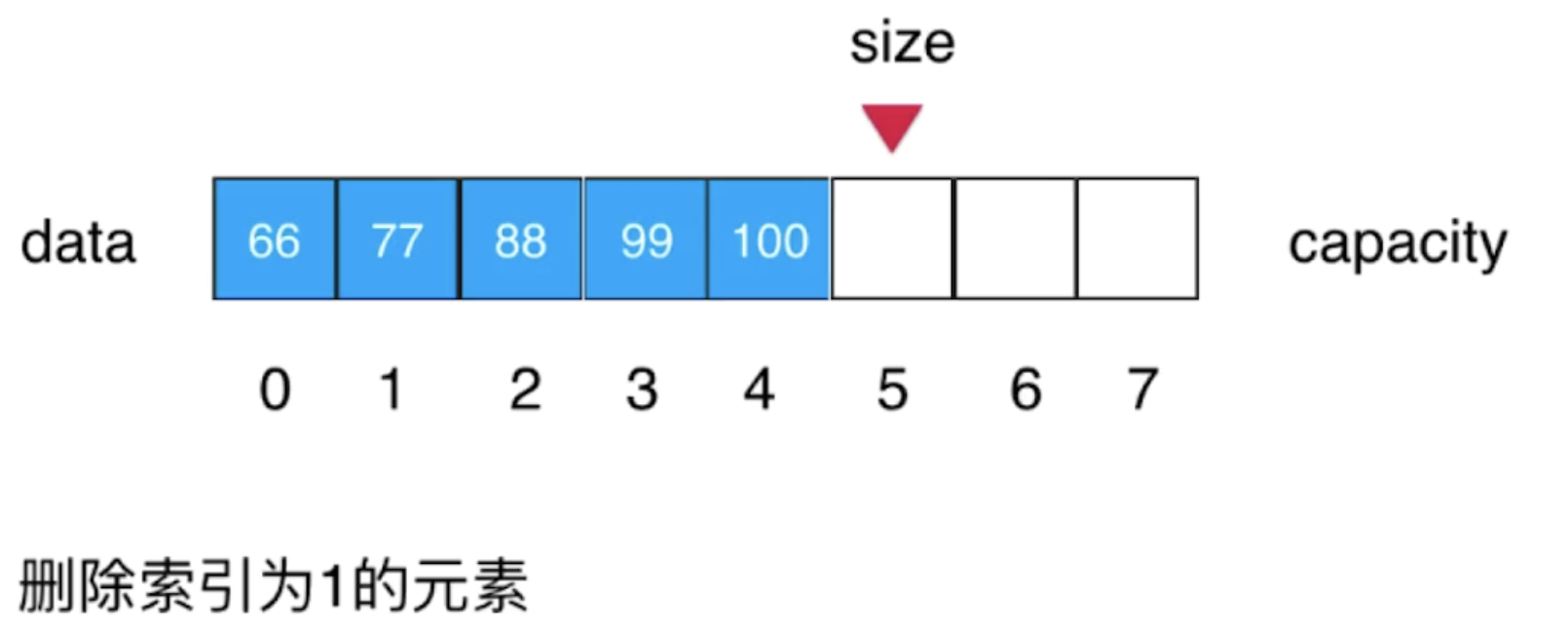
In fact, the deletion is similar to the insertion logic we implemented before, and the reverse is OK. As shown in the figure, for the element with index 1 to be deleted, we only need to move the element with index 2 to the left one grid to cover the element with index 1, then move the element with index 3 to the left one grid to cover the element with index 2, then move the element with index 4 to the left one grid to cover the element with index 3, and so on... Until all elements move to the left one grid, Add size-1. Finally, the element with the original index of 1 has been overwritten. There is no more 77 element in the array, which realizes the logic of deletion, as shown in the following figure:
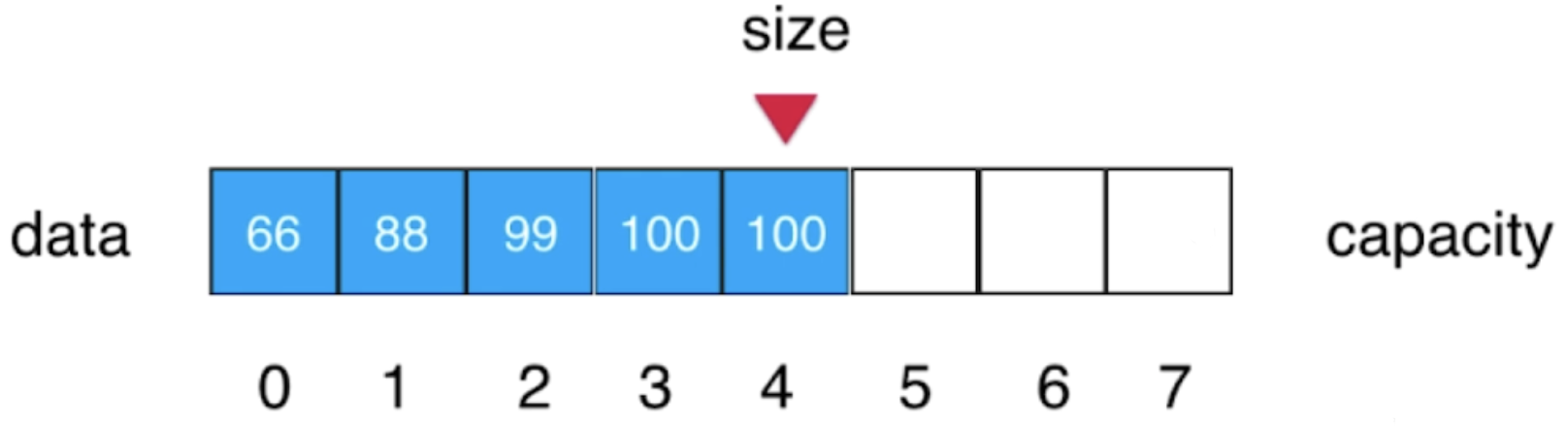
Some small partners may have questions. Will one more element in the last array have an impact? In fact, it will not have an impact, because the index position pointed to by size and the index position behind it are invisible to users. Moreover, the array will also have a default value during initialization. For example, the default value of int data is 0. Because the user can only access the elements he added to the array, and we also wrote a method to check the index in the previous section to ensure that the user's index is legal, the user does not know that there is an additional element here, There will be no impact. Of course, you can also empty the extra element after size-1. Finally, it should be mentioned that arrays of basic data types can be ignored, but if they are arrays of reference types, it is best to overwrite the extra elements with null, so that the data can be garbage collected quickly and the performance can be slightly optimized.
/**
* Delete the element at index position from the array and return the deleted element
*
* @param index index
* @return Deleted element
*/
public int remove(int index) {
checkIndex(index);
int ret = data[index];
for (int i = index + 1; i < size; i++) {
data[i - 1] = data[i];
}
// Similarly, you can directly use the array copy function to implement this logic
// System.arraycopy(data, index + 1, data, index, size - index + 1);
size--;
data[size] = 0;
return ret;
}
Based on this deletion method, we can also extend some convenient methods to users, as follows:
/**
* Deletes the first element from the array and returns the deleted element
*
* @return Deleted element
*/
public int removeFirst() {
return remove(0);
}
/**
* Deletes the last element from the array and returns the deleted element
*
* @return Deleted element
*/
public int removeLast() {
return remove(size - 1);
}
/**
* Remove element e from array
*
* @param e Elements to be deleted
* @return true will be returned if the deletion is successful, otherwise false will be returned
*/
public boolean removeElement(int e) {
int index = indexOf(e);
if (index != -1) {
remove(index);
return true;
}
return false;
}
/**
* Delete all elements e
*
* @param e Elements to be deleted
* @return true will be returned if the deletion is successful, otherwise false will be returned
*/
public boolean removeAllElement(E e) {
for (int i = 0; i < size; ) {
if (data[i] == e) {
remove(i);
} else {
i++;
}
}
return indexOf(e) == -1;
}
Use Generics
So far, our Array class can only store int type data, but as a container for storing data, it should not only store one type of data, but can store any type of data. In order for our Array class to store any type of data, we need to use generics in Java. However, you need to know that generics in Java can not receive basic data types, but only reference types. However, fortunately, the basic data types in java have their own wrapper classes. The so-called wrapper class is to encapsulate the basic types into a class so that generics can receive them.
public class Array<E> {
/**
* Array of actual data
*/
private E[] data;
/**
* Number of elements in the array
*/
private int size;
/**
* The capacity of the passed in Array is used to construct the Array
* So that users can customize the capacity of the array
*
* @param capacity capacity
*/
public Array(int capacity) {
// java syntax does not support direct new generics or generic arrays, so we need to first new an Object for strong conversion
data = (E[]) new Object[capacity];
size = 0;
}
public Array() {
// The default array capacity is 10
this(10);
}
/**
* Gets the number of elements in the array
*
* @return Number of elements in the array
*/
public int getSize() {
return size;
}
/**
* Gets the capacity of the array
*
* @return Capacity of the array
*/
public int getCapacity() {
return data.length;
}
/**
* Returns whether the array is empty
*
* @return If it is empty, return true; otherwise, return false
*/
public boolean isEmpty() {
return size == 0;
}
/**
* Adds a new element to the position of the last element + 1
*
* @param e New element
*/
public void addLast(E e) {
add(size, e);
}
/**
* Add a new element before all elements
*
* @param e New element
*/
public void addFirst(E e) {
add(0, e);
}
/**
* Insert a new element e under the index position
*
* @param index Indexes
* @param e New element
*/
public void add(int index, E e) {
// Throw an exception if the array is full
if (size == data.length) {
throw new IllegalArgumentException("Add failed. Array is full.");
}
// If the index is negative or the index is greater than size, an exception is thrown
// Because if the index is greater than size, the elements in the array will not have continuity, and if the index is less than 0, it is an invalid index
if (index < 0 || index > size) {
throw new IllegalArgumentException("Add failed. Require index >= 0 and index <= size.");
}
// The elements in the array are traversed from the last element until the index position pointed to by the index is reached
for (int i = size - 1; i >= index; i--) {
// Move each element back one bit
data[i + 1] = data[i];
}
// You can also directly use the function of array copy to implement this logic. Here, in order to indicate the logic of insertion, array copy is not used
// System.arraycopy(data, index, data, index + 1, size - index);
data[index] = e;
size++;
}
/**
* Gets the element at the index position
*
* @param index index
* @return index Element at index position
*/
public E get(int index) {
checkIndex(index);
return data[index];
}
/**
* Gets the last element in the array
*
* @return Last element
*/
public E getLast() {
return get(size - 1);
}
/**
* Gets the first element in the array
*
* @return First element
*/
public E getFirst() {
return get(0);
}
/**
* Modify the element of index position to e
*
* @param index index
* @param e e
*/
public void set(int index, E e) {
checkIndex(index);
data[index] = e;
}
/**
* Find whether there is an element e in the array
*
* @param e e
* @return true is returned, false is not returned
*/
public boolean contains(E e) {
int index = indexOf(e);
return index != -1;
}
/**
* Find the index of element e in the array. If element e does not exist, return - 1
*
* @param e e
* @return Index of element e, or - 1
*/
public int indexOf(E e) {
for (int i = 0; i < size; i++) {
if (data[i].equals(e)) {
return i;
}
}
return -1;
}
/**
* Deletes the element at the index position from the array and returns the deleted element
*
* @param index index
* @return Deleted element
*/
public E remove(int index) {
checkIndex(index);
E ret = data[index];
for (int i = index + 1; i < size; i++) {
data[i - 1] = data[i];
}
// Similarly, you can directly use the array copy function to implement this logic
// System.arraycopy(data, index + 1, data, index, size - index + 1);
size--;
data[size] = null;
return ret;
}
/**
* Deletes the first element from the array and returns the deleted element
*
* @return Deleted element
*/
public E removeFirst() {
return remove(0);
}
/**
* Deletes the last element from the array and returns the deleted element
*
* @return Deleted element
*/
public E removeLast() {
return remove(size - 1);
}
/**
* Remove element e from array
*
* @param e Elements to be deleted
* @return true will be returned if the deletion is successful, otherwise false will be returned
*/
public boolean removeElement(E e) {
int index = indexOf(e);
if (index != -1) {
remove(index);
return true;
}
return false;
}
/**
* Delete all elements e
*
* @param e Elements to be deleted
* @return true will be returned if the deletion is successful, otherwise false will be returned
*/
public boolean removeAllElement(E e) {
for (int i = 0; i < size; ) {
if (data[i] == e) {
remove(i);
} else {
i++;
}
}
return indexOf(e) == -1;
}
@Override
public String toString() {
if (isEmpty()) {
return "[]";
}
StringBuilder sb = new StringBuilder();
sb.append(String.format("Array: size = %d, capacity = %d\n", size, data.length));
sb.append("[");
for (int i = 0; i < size; i++) {
sb.append(data[i]);
if (i != size - 1) {
sb.append(", ");
}
}
return sb.append("]").toString();
}
/**
* Check whether the index is legal
*
* @param index index
*/
private void checkIndex(int index) {
// If the index is negative or the index is greater than or equal to size, an exception is thrown
// Because when the index is greater than or equal to size, users will access invalid data, and when the index is less than 0, it is an invalid index
if (index < 0 || index >= size) {
throw new IllegalArgumentException("Require index >= 0 and index <= size.");
}
}
}
Dynamic array
By introducing generics, our Array can now store any type of data, and the basic addition, deletion, query and modification methods have been implemented earlier. Now there is only one last problem. The Array inside Array is still a static Array, and the capacity of the static Array is limited, and the size has been set at the time of initialization and cannot be changed. In actual development, we usually can't determine the size of the Array. We hope that when the Array capacity is full, we can automatically expand the capacity instead of throwing an Array out of bounds exception, so we need to implement a dynamic Array.
In fact, the idea of realizing dynamic capacity expansion is also very simple. When the array capacity is found to be full when adding elements, create an array with larger capacity, for example, create a new array twice as large as the original array (1.5 times in ArrayList), then copy all the elements of the old array to the new array, and then point the reference of data to the new array, At this time, the old array will lose its reference and be garbage collected. In this way, the expansion is completed. The rest of the logic is the same as before. Just add the new element to the data as usual.
/**
* Reset array capacity
*
* @param newCapacity New capacity
*/
private void resize(int newCapacity) {
E[] newData = (E[]) new Object[newCapacity];
for (int i = 0; i < size; i++) {
newData[i] = data[i];
}
// You can use array copy directly
// System.arraycopy(data, 0, newData, 0, size);
data = newData;
}
Then modify the method of adding elements as follows:
/**
* Insert a new element e under the index position
*
* @param index Indexes
* @param e New element
*/
public void add(int index, E e) {
// If the index is negative or the index is greater than size, an exception is thrown
// Because if the index is greater than size, the elements in the array will not have continuity, and if the index is less than 0, it is an invalid index
if (index < 0 || index > size) {
throw new IllegalArgumentException("Add failed. Require index >= 0 and index <= size.");
}
// If the array is full, expand the capacity
if (size == data.length) {
resize(data.length * 2);
}
// The elements in the array are traversed from the last element until the index position pointed to by the index is reached
for (int i = size - 1; i >= index; i--) {
// Move each element back one bit
data[i + 1] = data[i];
}
// You can also directly use the function of array copy to implement this logic. Here, in order to indicate the logic of insertion, array copy is not used
// System.arraycopy(data, index, data, index + 1, size - index);
data[index] = e;
size++;
}
When deleting elements, we also want to reduce the capacity when the elements in the array are less than half of the capacity of the array. Similarly, we only need to call the previously written resize method. The code for modifying the remove method is as follows:
/**
* Delete the element at index position from the array and return the deleted element
*
* @param index index
* @return Deleted element
*/
public E remove(int index) {
checkIndex(index);
E ret = data[index];
for (int i = index + 1; i < size; i++) {
data[i - 1] = data[i];
}
// Similarly, you can directly use the array copy function to implement this logic
// System.arraycopy(data, index + 1, data, index, size - index + 1);
size--;
data[size] = null;
// Judge whether it is necessary to shrink the volume. Here, 1 / 4 of the volume is reduced to avoid complexity fluctuation
if (size == data.length / 4 && data.length / 2 != 0) {
resize(data.length / 2);
}
return ret;
}
Time complexity comparison
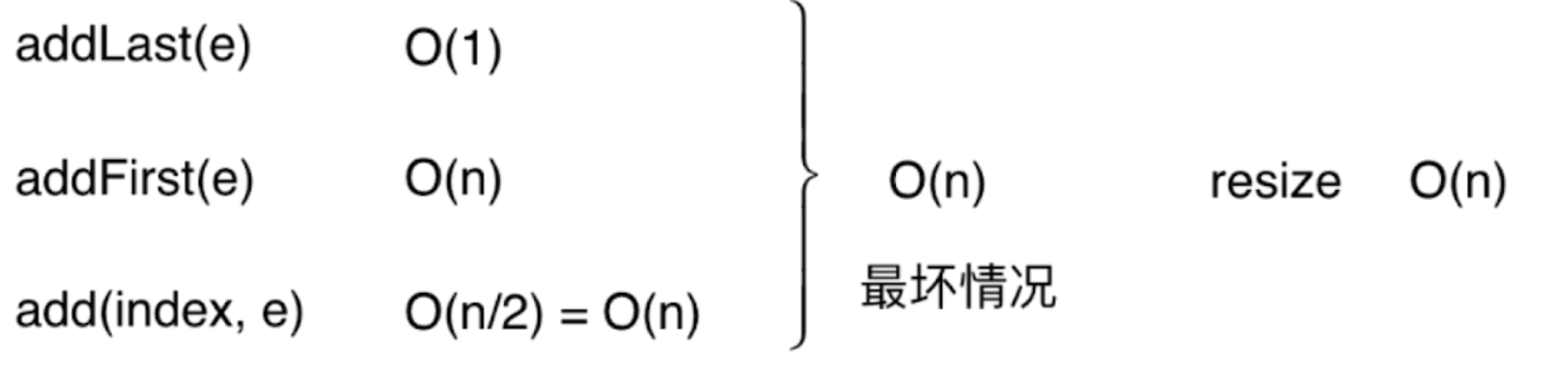
addLast(e): because this method only adds an element at the end of the array, because there is only one operation, the complexity is O(1). Some people may say that addLast calls add and will trigger resize when the array is full, and the complexity of resize is O(n). Why is the complexity of addLast still O(1)? This is because resize does not happen every time, and the trigger of resize is not unpredictable. We can know exactly when it will trigger resize and how many times it will expand, so we should share the complexity equally. Assuming that the current capacity = 8, and each addition operation is to addLast, when the ninth addLast operation is performed, resize is triggered, and a total of 17 basic operations are performed (twice the resizing capacity). On average, two basic operations are performed for each addLast operation. In this way, the time complexity is O(1). In this case, the calculation of equal share is more meaningful than the calculation of the worst case
addFirst(e): this method adds elements to the front of the array, and then the remaining N elements in the array need to be moved to the right one grid, so the complexity is O(n)
add(index, e): the complexity of this method is closely related to the value of index. When the value of index is 0, the complexity is the same as addFirst. When the value of index is size, the complexity is the same as addLast. The index value range is the number of elements in the array, so the possibility of each index being specified is equal. Complexity analysis is to analyze the complexity in the worst case. The worst case of the add method is that the index is 0, because when the index is 0, all elements in the array need to be moved, so the complexity is the same as addFirst, which is O(n)
set(index, e): the complexity of modifying elements according to the index is obviously O(1), because array elements can be accessed / manipulated directly through the index
get(index): similarly, this method obtains elements directly according to the index, and the complexity is O(1)
contains(e): without knowing the index, we can only judge whether the array contains an element by traversing the array elements, so the complexity is O(n)
indexOf(e): the index of the query element is the same. In the worst case, the entire array needs to be traversed, and the complexity is O(n)
Based on the worst case, the complexity of our addition operation is O(N):
The delete operation is logically similar to the add operation, so the comprehensive time complexity of the delete operation is also O(N):
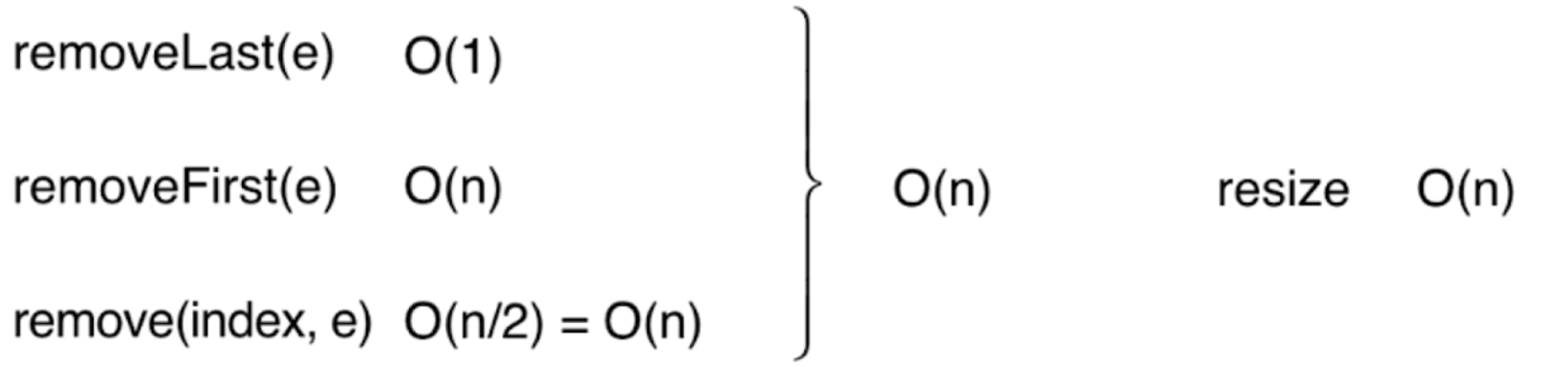
Summary of comprehensive time complexity of main methods of dynamic array:
- Add: O(n)
- Delete: O(n)
- Change: known index O(1); Unknown index O(n)
- Check: known index O(1); Unknown index O(n)
Source code address: https://github.com/perkinls/java-summary/tree/master/02-data-structure/src/main/java/lipan/top/notes/datastructure/array