Segment tree of advanced data structure

1. Prefix and

Given an array arr, the array can be very large. During the running of the program, you may have to do several query and update operations: query(arr, L, R) means to calculate the sum of all numbers from subscript L to subscript r in the array arr. update(arr, i, val) means to change the number in arr[i] to val. How to complete a series of query and update operations as quickly as possible?

If it is prefix sum, the time complexity of query is optimized to O (1), while the operation of update is still O (n). A bit updates a certain value, and all the presum of the interval should be updated

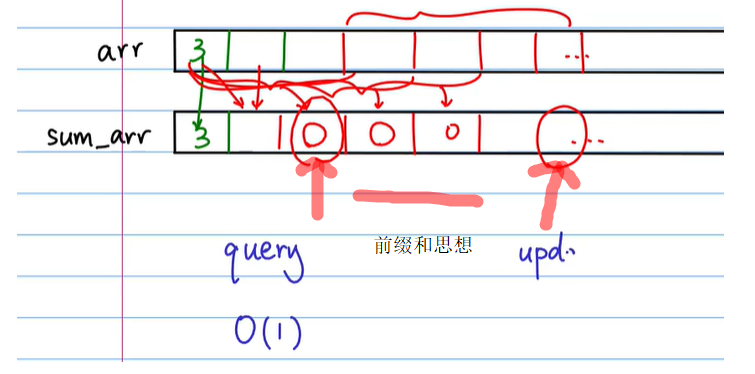
So how to reduce the time complexity of update? At the same time, the time complexity of query will not be too high? Both query and log operations can turn them into log

2. What is a segment tree?

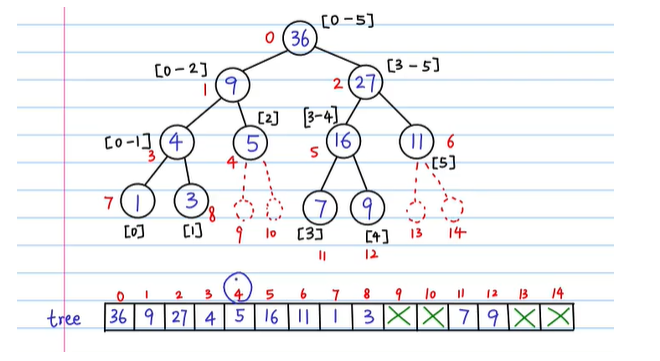
Segment tree is a binary search tree, which is similar to interval tree. It divides an interval into some unit intervals, and each unit interval corresponds to a leaf node in the segment tree. Using the segment tree, you can quickly find the number of occurrences of a node in several segments, and the time complexity is O(logN). The space complexity of the unoptimized is 2N. In practical application, it is generally required to open 4N (if the leaf node is n, then the number of nodes in the whole tree is 2^h - 1, 2^(h - 1) = n. in case of crossing the boundary, the left and right free nodes of the leaf node also need space, so it is 2n + 2n = 4n) array to avoid crossing the boundary. Therefore, it is sometimes necessary to discretize to compress the space.

For each non leaf node [a,b] in the segment tree, the interval represented by its left son is [a,(a+b)/2], and the interval represented by its right son is [(a+b)/2+1,b]. Therefore, the segment tree is a balanced binary tree, and the last number of sub nodes is N, that is, the length of the whole segment interval.

As shown in the figure below, the whole interval is continuously divided into several intervals. Each non leaf node represents the sum of an interval, and the leaf node is the value of the corresponding subscript of arr

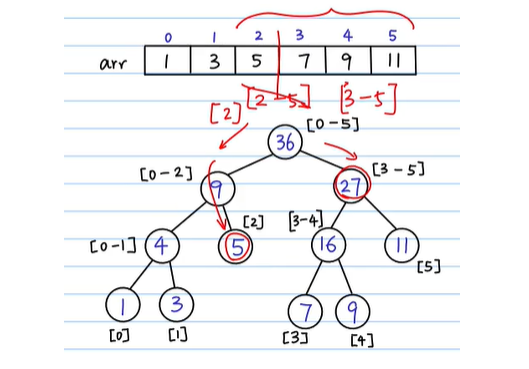
Relationship between array subscript and value of segment tree

3. How to build a segment tree?

Tip: the search interval in the code is [start, end], and the range of the array is [l, r], which is opposite to the figure

1. Establish a tree

The idea of recursion is from top to bottom. The value of the parent node of each tree is the sum of the left and right child nodes. Therefore, the idea of recursion can be adopted. The boundary is l == r, which means that the interval returns with only one value, and the interval and bottom-up are constantly updated

public void buildTree(int[] tree, int[] data, int l, int r, int treeIndex){
    if(l == r){
       tree[treeIndex] = data[r];
        return;
    }
    int mid = (l + r) / 2;
    //Index of child nodes
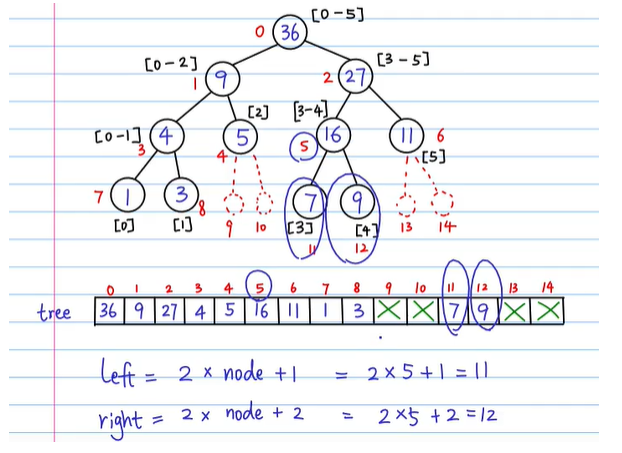
    int leftIndex = 2 * treeIndex + 1;
    int rightIndex = 2 * treeIndex + 2;
    buildTree(tree, data, l, mid, leftIndex);
    buildTree(tree, data, mid + 1, r, rightIndex);
    tree[treeIndex] = tree[leftIndex] + tree[rightIndex];
}

2. Modify tree

We must first know which half of the tree the index to be modified is in, and then use the idea of recursion to modify it and update it from bottom to top

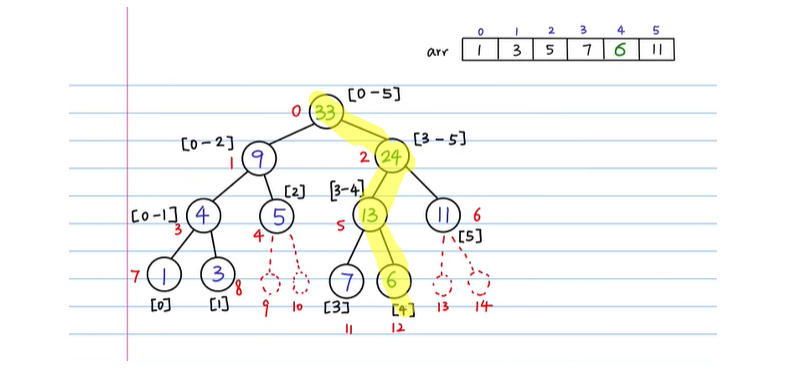
public void updateTree(int[] tree, int[] data, int l, int r, int treeIndex, int val, int index){
    if(l == r){
        data[l] = val;
       	tree[treeIndex] = val;
        return;
    }
    int mid = (l + r) / 2;
    int leftIndex = 2 * treeIndex + 1;
    int rightIndex = 2 * treeIndex + 2;
    //Recursive left and right subtree
    if(index >= l && index <= mid){
        updateTree(tree, data, l, mid, leftIndex, val, index);
    }else{
        updateTree(tree, data, mid + 1, r, val, index);
    }
    //Constantly update upward
    tree[treeIndex] = tree[leftIndex] + tree[rightIndex];
}

3. Find the corresponding value

1. The range [L,R] of the queried interval is not within the range of the array, indicating that the interval does not coincide. If there is no coincidence, there will be no value even if you continue to recurse, so you need to return 0 at this time

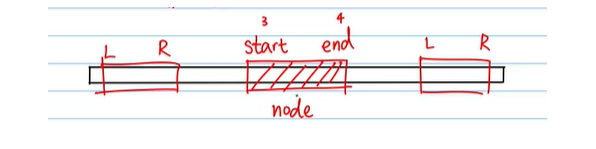
2. When l == r, it means that there is only one value in a half area. When l < = start end < = R, it means that the interval coverage directly returns the value of the current tree root node

For example, if we find the interval [2,5], then when l == r, the left half will find [2,2] and the right half will find [3,5]

3. The array range is included in the search interval and directly returns the tree node value. Still take [2,5] as an example. When the right half is an interval [3,5], which is included in the whole interval [2,5] I need to find, then the value of the interval [3,5] can be returned directly at this time. Otherwise, it will continue to recursively search the left and right subtrees, and then there will be repeated calculations. Then the non leaf nodes of the tree will be meaningless, so we must reduce branches in advance and return

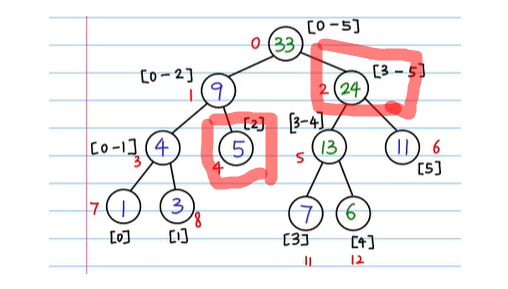
As shown in the figure, there is no pruning in advance

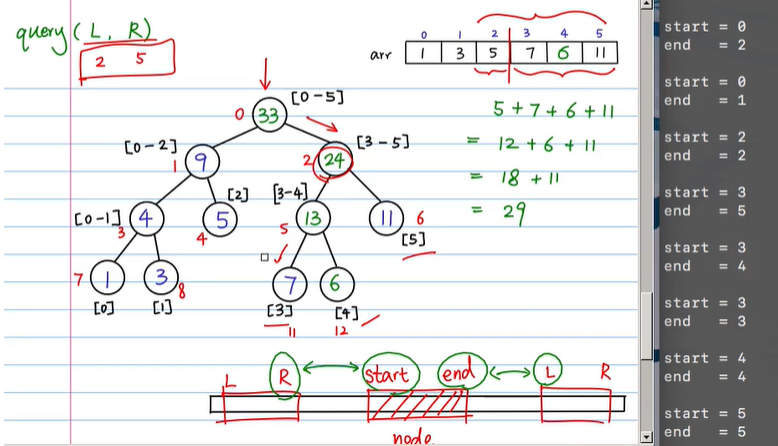
(the interval searched by the code is [start, end], corresponding to [l, r] in the figure, and the array range [l, r] corresponds to [start, end] in the figure, just the opposite)

It will recurse to the root node until l == r, so you can subtract branches in advance and add this termination condition: if (start < = L & & R < = end) return tree [treeindex];

//start end is the array range to be searched, and l and R are the length range of the array
public int queryTree(int[] tree, int treeIndex, int l, int r, int start, int end){
        if(l > end || r < start)return 0;//0 if out of range
        //Leaf node
        if(l == r)return tree[treeIndex];
        
        //If the current L and R fall within the query interval, the current node will be returned directly, indicating a part of the interval sum
    	//Without this step, the calculation will be repeated
        if(start <= l && r <= end)return tree[treeIndex];

        int mid = (l + r) / 2;
        int leftIndex = 2 * treeIndex + 1;
        int rightIndex = 2 * treeIndex + 2;
        int leftSum = queryTree(tree, leftIndex, l, mid, start, end);
        int rightSum = queryTree(tree, rightIndex, mid + 1, r, start, end);
        return leftSum + rightSum;
    }

4.LeetCode

307. Area and retrieval - array modifiable

class NumArray {
    private int[] data;
    private int[] tree;
    public NumArray(int[] nums) {
        this.data = nums;
        this.tree = new int[nums.length * 4];
        buildTree(0, 0, nums.length - 1);
    }
    
    
    public void buildTree(int treeIndex, int l, int r){
        if(l == r){
            tree[treeIndex] = data[l];//Leaf node
            return;
        }

        int mid = (l + r) / 2;
        int leftIndex = 2 * treeIndex + 1;
        int rightIndex = 2 * treeIndex + 2;
        buildTree(leftIndex, l, mid);
        buildTree(rightIndex,mid + 1, r);
        tree[treeIndex] = tree[leftIndex] + tree[rightIndex];

    }


    public void update(int index, int val){
        updateTree(0, 0, data.length - 1, index, val);
    }

    public void updateTree(int treeIndex, int l, int r, int index, int val){
        if(l == r && l == index){
            data[index] = val;
            tree[treeIndex] = val;
            return;
        }

        int mid = (l + r) / 2;
        int leftIndex = 2 * treeIndex + 1;
        int rightIndex = 2 * treeIndex + 2;
        if(index >= l && index <= mid){
            updateTree(leftIndex, l, mid, index, val);
        }else{
            updateTree(rightIndex, mid + 1, r, index, val);
        }
        tree[treeIndex] = tree[leftIndex] + tree[rightIndex];
    }



    public int sumRange(int start, int end){
        return queryTree(0, 0, data.length - 1, start, end);
    }

    public int queryTree(int treeIndex, int l, int r, int start, int end){
        if(l > end || r < start)return 0;
        if(l == r)return tree[treeIndex];
        if(start <= l && r <= end)return tree[treeIndex];

        int mid = (l + r) / 2;
        int leftIndex = 2 * treeIndex + 1;
        int rightIndex = 2 * treeIndex + 2;
        int leftSum = queryTree(leftIndex, l, mid, start, end);
        int rightSum = queryTree(rightIndex, mid + 1, r, start, end);
        return leftSum + rightSum;
    }
}