Special topic of line segment tree (I): basic application
——Record of the fourth IQ crisis
In ancient times, there was a full array simulation one night and I didn't understand it at all. Today, there is a line segment tree course for two days and I don't understand it at all
Preliminary in a line segment tree
1 before starting: why, what is it
Segment tree, as its name suggests, is to split a segment into a tree.
More specifically, it is a binary tree.
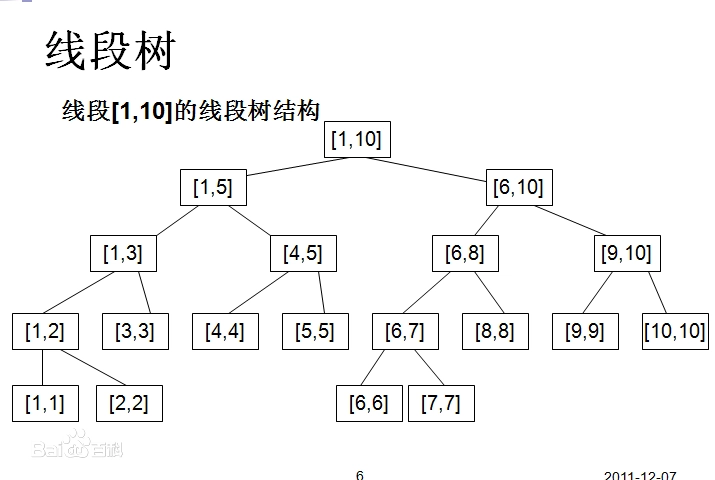
So what's the point of doing this?
Obviously, if this sequence becomes this form, according to the basic knowledge of multiplication, the number of times we find a specific point or a specific interval will become logn times, and the number of times we need to modify a point or an interval will also become logn times. The time saved from n to logn is very huge (exponential optimization), so the segment tree can save a lot of time on interval maintenance and interval query.
In this way, the application scope and functions of segment tree are clear: interval maintenance and interval query.
In this part, we will discuss the basic functions of line segment tree.
2. Start: interval check and modification
Interval checking and modification is the best place to reflect the advantages of line segment tree. After all, the general single point checking and modification of line segment is O(1), which is actually faster than line segment tree (nonsense). In that case, it must start with interval check and change.
Sum the most basic interval first
T1 segment tree 1 (Luogu P3372, difficulty 1)
Analyze the functional modules needed to complete this task.
First, if we have a given sequence at the beginning, we must make achievements;
Second, we need to check and modify the interval, and there must be modification and query.
It's over.
Specifically study how to write these three things.
First of all, according to this structure, recursive operations must be performed. Since each segment is composed of the data on the left and right sides (hereinafter referred to as the left and right sons), the left and right sons must be recursive. As for the numbers of the left and right sons, according to the theory of binary tree, it's K < < 1 and K < < 1 | 1.
Friendly tip: k | 1 is not equal to k+1. The reason why we can use bit operation here is that the rightmost bit must be 0 after moving left
Think again about the boundary. Building a tree is essentially a single point modification, so the boundary is l==r; For interval operation, if the current query interval is included in the target interval, the result will be returned directly without further query; Otherwise, according to the characteristics of the left and right sons, if there is an intersection between the query interval and the left half of the target interval, we will query the left son, and the same is true on the other side.
In this way, the rudiment of the line segment tree basically comes out.
Consider whether there is a better processing method: since we change the query interval to the interval, if the query interval is already included in the target interval, we don't have to change the smaller interval. For example, if we add 3 to each number of 1 ~ 5 and query 1 ~ 5, we don't need to deal with 1 ~ 2, 3 ~ 5 and smaller intervals. In this way, we can mark the content to be updated to indicate that a modification stays in a certain position. If we are going to continue to query our son, we will update this modification to our son. This tag is called lazy tag.
Obviously, lazy tag passing is also a functional module. In this way, the segment tree involved in this problem has four modules: tree building, tag transfer, modification and query (from top to bottom). This problem is finished.
Note one detail: the array related to the line segment tree should be opened to 4n.
The code is as follows:
#include<cstdio>
#include<cstring>
#include<algorithm>
#Define mid (L + R > > 1) / / Note: the brackets are outside
using namespace std;
long long a[1000001];
struct yjx{
long long tre[1000001],laz[1000001];
void build(int k,int l,int r){
if(l == r){
tre[k] = a[l];
return;
}
build(k << 1,l,mid),build(k << 1 | 1,mid + 1,r);
tre[k] = tre[k << 1] + tre[k << 1 | 1];
}
void push(int k,int l,int r){
laz[k << 1] += laz[k],laz[k << 1 | 1] += laz[k];
tre[k << 1] += laz[k] * (mid - l + 1),tre[k << 1 | 1] += laz[k] * (r - mid);
laz[k] = 0;//Be sure to empty it
}
void change(int k,int l,int r,int x,int y,long long c){
if(x <= l && r <= y){
tre[k] += (r - l + 1) * c;
laz[k] += c;
return;
}
push(k,l,r);
if(x <= mid) change(k << 1,l,mid,x,y,c);
if(y > mid) change(k << 1 | 1,mid + 1,r,x,y,c);
tre[k] = tre[k << 1] + tre[k << 1 | 1];
}
long long query(int k,int l,int r,int x,int y){
long long ret = 0;
if(x <= l && r <= y) return tre[k];
push(k,l,r);
if(x <= mid) ret += query(k << 1,l,mid,x,y);
if(y > mid) ret += query(k << 1 | 1,mid + 1,r,x,y);
return ret;
}
}STr;
int main(){
int m,n,i,x,y,z;
long long w;
scanf("%d %d",&n,&m);
for(i = 1;i <= n;i++) scanf("%lld",&a[i]);
STr.build(1,1,n);
for(i = 1;i <= m;i++){
scanf("%d",&z);
if(z == 1){
scanf("%d %d %lld",&x,&y,&w);
STr.change(1,1,n,x,y,w);
}
if(z == 2){
scanf("%d %d",&x,&y);
printf("%lld\n",STr.query(1,1,n,x,y));
}
}
return 0;
}
(Note: the function in the structure is referenced in the structure without structure prefix)
3. Application of lazy marks
The essence of lazy tags is actually maintenance. As the segment tree problem is different, the lazy tag will certainly be different. So are there any limitations in the use of lazy tags?
In order to understand this problem, we need to consider how lazy tags are passed. The objects of transmission are nothing more than two: left and right sons and lazy marks of left and right sons.
Here are some examples:
(1) Without any modification, the lazy tag is obviously useless (it is impossible without query, otherwise it will be lonely).
(2) Single click modification. Just change it directly. There is no need for lazy tags.
(3) Interval modulus, interval square,... Can not be maintained at all, or it is a fixed value, which is not necessary to maintain.
To sum up, lazy tags are applicable to the interaction between variables in interval modification, such as five basic operations. The rest should seek other optimization methods or direct violent modification.
What if several operations need to be marked?
T2 segment tree 2 (Luogu P3373, difficulty 2.5)
Interval addition, interval multiplication, interval summation.
The operation itself is not difficult. The key is how to pass the lazy mark.
First, lazy tags can be passed together. There is no need to write two push functions.
Secondly, if you want to update the lazy mark of multiplication and addition for your son, it must be multiplication before addition. Here, we don't need to worry about what to do if we first add an interval and then multiply it, because the previous mark should have been passed long ago. We only need to consider the priority of the four operations themselves.
Thirdly, if we want to pass the lazy marks of the left and right sons, we should pay attention to that the lazy marks are the information to be transmitted next. Therefore, in the simple transmission of lazy marks, the lazy marks also need to be calculated. For example, if you give the same interval + 3 and * 2 successively, the original + 3 mark should become + 6 when multiplying.
In this way, we can conclude that lazy tags operate according to priority in the process of transferring tags and updating, and there will be interaction between lazy tags (high-level impact and low-level impact).
The code is as follows:
#include<cstdio>
#include<cstring>
#include<algorithm>
#define mid (l + r >> 1)
using namespace std;
long long p,a[1000001];
struct yjx{
long long tre[1000001],laz1[1000001],laz2[1000001];
void build(int k,int l,int r){
laz2[k] = 1;
if(l == r){
tre[k] = a[l] % p;
return;
}
build(k << 1,l,mid),build(k << 1 | 1,mid + 1,r);
tre[k] = (tre[k << 1] + tre[k << 1 | 1]) % p;
}
void push(int k,int l,int r){
tre[k << 1] = (tre[k << 1] * laz2[k] + laz1[k] * (mid - l + 1)) % p;
tre[k << 1 | 1] = (tre[k << 1 | 1] * laz2[k] + laz1[k] * (r - mid)) % p;
laz1[k << 1] = (laz1[k << 1] * laz2[k] + laz1[k]) % p;
laz1[k << 1 | 1] = (laz1[k << 1 | 1] * laz2[k] + laz1[k]) % p;
laz2[k << 1] = (laz2[k << 1] * laz2[k]) % p;
laz2[k << 1 | 1] = (laz2[k << 1 | 1] * laz2[k]) % p;
laz1[k] = 0;
laz2[k] = 1;
}
void change1(int k,int l,int r,int x,int y,int c){
if(x <= l && r <= y){
tre[k] = (tre[k] + (r - l + 1) * c) % p;
laz1[k] = (laz1[k] + c) % p;
return;
}
push(k,l,r);
if(x <= mid) change1(k << 1,l,mid,x,y,c);
if(y > mid) change1(k << 1 | 1,mid + 1,r,x,y,c);
tre[k] = (tre[k << 1] + tre[k << 1 | 1]) % p;
}
void change2(int k,int l,int r,int x,int y,int c){
if(x <= l && r <= y){
tre[k] = tre[k] * c % p;
laz1[k] = laz1[k] * c % p;
laz2[k] = laz2[k] * c % p;
return;
}
push(k,l,r);
if(x <= mid) change2(k << 1,l,mid,x,y,c);
if(y > mid) change2(k << 1 | 1,mid + 1,r,x,y,c);
tre[k] = (tre[k << 1] + tre[k << 1 | 1]) % p;
}
long long query(int k,int l,int r,int x,int y){
long long ret = 0;
if(x <= l && r <= y) return tre[k];
push(k,l,r);
if(x <= mid) ret = (ret + query(k << 1,l,mid,x,y)) % p;
if(y > mid) ret = (ret + query(k << 1 | 1,mid + 1,r,x,y)) % p;
return ret;
}
}STr;
int main(){
int m,n,i,j,k,x,y,w;
scanf("%d %d %lld",&n,&m,&p);
for(i = 1;i <= n;i++) scanf("%lld",&a[i]);
STr.build(1,1,n);
for(i = 1;i <= m;i++){
scanf("%d",&k);
if(k == 1){
scanf("%d %d %d",&x,&y,&w);
STr.change2(1,1,n,x,y,w);
}
if(k == 2){
scanf("%d %d %d",&x,&y,&w);
STr.change1(1,1,n,x,y,w);
}
if(k == 3){
scanf("%d %d",&x,&y);
printf("%lld\n",STr.query(1,1,n,x,y));
}
}
return 0;
}
(Note: when the multiplication lazy flag is cleared, it should be 1, and the initial value should also be 1, so it needs to be initialized)
Application of two basic line segment tree
1. Various basic operations and optimization
After being familiar with some basic operations of line segment tree, let's study how to flexibly use the function of section query and modification of line segment tree to complete some basic operations.
T3 gcd interval (Luogu P1890, difficulty 1.5)
Only interval gcd query.
This question is purely for hands-on practice.
First of all, there is no modification operation, no lazy tag is required, and only tree creation and query are required;
Secondly, the interval gcd can be obtained by taking gcd from several numbers in the interval, and then taking gcd... Repeatedly. Therefore, the segment tree can maintain the gcd result.
The code is as follows:
#include<cstdio>
#include<cstring>
#include<algorithm>
#define mid (l + r >> 1)
using namespace std;
int a[1000001];
int gcd(int x,int y){
if(x % y) return gcd(y,x % y);
else return y;
}
struct yjx{
int tre[4000001],laz[4000001];
void build(int k,int l,int r){
if(l == r){
tre[k] = a[l];
return;
}
build(k << 1,l,mid);
build(k << 1 | 1,mid + 1,r);
tre[k] = gcd(tre[k << 1],tre[k << 1 | 1]);
}
int query(int k,int l,int r,int x,int y){
if(x <= l && r <= y) return tre[k];
int ret = 0;
if(x <= mid) ret = query(k << 1,l,mid,x,y);
if(y > mid) ret = gcd(ret,query(k << 1 | 1,mid + 1,r,x,y));
return ret;
}
}STr;
int main(){
int i,j,k,m,n,l,r;
scanf("%d %d",&n,&m);
for(i = 1;i <= n;i++) scanf("%d",&a[i]);
STr.build(1,1,n);
for(i = 1;i <= m;i++){
scanf("%d %d",&l,&r);
printf("%d\n",STr.query(1,1,n,l,r));
}
return 0;
}
T4 The Child and Sequence (Luogu CF438D, difficulty 2.5)
Interval modulus, single point modification, interval summation.
Let's first consider the lazy mark: the interval module cannot be marked, and the single point modification does not need to be marked, so the lazy mark is not needed for this problem.
What about the operation of interval mold taking? It's very simple. When l==r, just click Modify.
But in this way, there will be a lot of operations. We have to consider how to take a few modules less. If all the numbers in an interval are less than the modulus, there is no need to take the modulus. In this way, we need to maintain a maximum value to judge whether it is necessary to take the mold. This maintenance itself will not produce any time complexity. In this way, the purpose of optimization is achieved, and the problem can be passed.
In general, if there is no lazy tag to play, optimization should be considered from the perspective of how to avoid operation.
The code is as follows:
#include<cstdio>
#include<cstring>
#include<algorithm>
using namespace std;
#define mid (l + r >> 1)
long long a[100001],tre[400001],mx[400001];
struct yjx{
void build(int k,int l,int r){
if(l == r){
tre[k] = mx[k] = a[l];
return;
}
build(k << 1,l,mid);
build(k << 1 | 1,mid + 1,r);
tre[k] = tre[k << 1] + tre[k << 1 | 1];
mx[k] = max(mx[k << 1],mx[k << 1 | 1]);
}
void modify(int k,int l,int r,int x,int c){
if(l == r){
tre[k] = mx[k] = c;
return;
}
if(x <= mid) modify(k << 1,l,mid,x,c);
else modify(k << 1 | 1,mid + 1,r,x,c);
tre[k] = tre[k << 1] + tre[k << 1 | 1];
mx[k] = max(mx[k << 1],mx[k << 1 | 1]);
}
void momodify(int k,int l,int r,int x,int y,int p){
if(mx[k] < p) return;
if(l == r){
tre[k] %= p;
mx[k] %= p;
return;
}
if(x <= mid) momodify(k << 1,l,mid,x,y,p);
if(y > mid) momodify(k << 1 | 1,mid + 1,r,x,y,p);
tre[k] = tre[k << 1] + tre[k << 1 | 1];
mx[k] = max(mx[k << 1],mx[k << 1 | 1]);
}
long long query(int k,int l,int r,int x,int y){
if(x <= l && r <= y) return tre[k];
long long ret = 0;
if(x <= mid) ret += query(k << 1,l,mid,x,y);
if(y > mid) ret += query(k << 1 | 1,mid + 1,r,x,y);
return ret;
}
}STr;
int main(){
int i,m,n,w,x,y,z;
scanf("%d %d",&n,&m);
for(i = 1;i <= n;i++) scanf("%lld",&a[i]);
STr.build(1,1,n);
for(i = 1;i <= m;i++){
scanf("%d",&z);
if(z == 1){
scanf("%d %d",&x,&y);
printf("%lld\n",STr.query(1,1,n,x,y));
}
if(z == 2){
scanf("%d %d %d",&x,&y,&w);
STr.momodify(1,1,n,x,y,w);
}
if(z == 3){
scanf("%d %d",&x,&w);
STr.modify(1,1,n,x,w);
}
}
return 0;
}
(Note: you can consider inserting the updates of tre[k] and mx[k] at the end of all functions into one function pushup(k))
There is another similar question:
T5 flower god travels around countries (Luogu P4145, difficulty 2.5)
The interval is squared and the interval is summed.
Basically the same as the previous question, there is no lazy mark. This reduction method is also easy. Because rounding down is still the maximum value of the additional maintenance interval, if it is less than or equal to 1, it will not be modified.
Attach the code of the modified part:
#include<cstdio>
#include<cstring>
#include<algorithm>
#include<cmath>
using namespace std;
#define mid (l + r >> 1)
long long a[100001],tre[400001],mx[400001];
void modify(int k,int l,int r,int x,int y){
if(mx[k] <= 1) return;
if(l == r){
tre[k] = sqrt(tre[k]);
mx[k] = sqrt(mx[k]);
return;
}
if(x <= mid) modify(k << 1,l,mid,x,y);
if(y > mid) modify(k << 1 | 1,mid + 1,r,x,y);
tre[k] = tre[k << 1] + tre[k << 1 | 1];
mx[k] = max(mx[k << 1],mx[k << 1 | 1]);
}
The above questions do not need to be marked with laziness. Here are two questions that need to be marked with laziness:
T6 interval plus sin sum of interval (Luogu P6327, difficulty 3)
The operation is shown in the question.
This question has interval addition, so this addend can be lazy marked for optimization.
Consider sin and how to maintain it. First of all, you have to learn the trigonometric function of the first unit of compulsory three. There is such a formula:
sin(α+β) = sinαcosβ + cosαsinβ
cos(α+β) = cosαcosβ - sinαsinβ
So we maintain sin sum and cos sum for a given sin α, If a new one is added β, These two formulas can be used to update. It is proved that for an interval sin and stre[k] and an interval cos and ctre[k], if you add β, The above two equations are still satisfied, namely:
stre[k] = stre[k] * cos(laz[k]) + ctre[k] * sin(laz[k]); ctre[k] = ctre[k] * cos(laz[k]) - stre[k] * sin(laz[k]);
However, it should be noted that the stre and ctre we use when updating are before the update. That is to say, if we write like this, it is wrong because stre has been updated. And the two are used for each other, which cannot be solved by simple sequence adjustment, so it is necessary to operate as follows:
double temp = stre[k]; stre[k] = stre[k] * cos(laz[k]) + ctre[k] * sin(laz[k]); ctre[k] = ctre[k] * cos(laz[k]) - temp * sin(laz[k]);
The rest is the basic operation of line segment tree.
The code is as follows:
#include<cstdio>
#include<cstring>
#include<algorithm>
#include<cmath>
#define mid (l + r >> 1)
using namespace std;
double a[200001];
struct yjx{
double stre[800001],ctre[800001];
long long laz[800001];
void build(int k,int l,int r){
if(l == r){
stre[k] = sin(a[l]);
ctre[k] = cos(a[l]);
return;
}
build(k << 1,l,mid),build(k << 1 | 1,mid + 1,r);
stre[k] = stre[k << 1] + stre[k << 1 | 1];
ctre[k] = ctre[k << 1] + ctre[k << 1 | 1];
}
void push(int k,int l,int r){
double temp = stre[k << 1];
if(!laz[k]) return;
laz[k << 1] += laz[k],laz[k << 1 | 1] += laz[k];
stre[k << 1] = stre[k << 1] * cos(laz[k]) + ctre[k << 1] * sin(laz[k]);
ctre[k << 1] = ctre[k << 1] * cos(laz[k]) - temp * sin(laz[k]);
temp = stre[k << 1 | 1];
stre[k << 1 | 1] = stre[k << 1 | 1] * cos(laz[k]) + ctre[k << 1 | 1] * sin(laz[k]);
ctre[k << 1 | 1] = ctre[k << 1 | 1] * cos(laz[k]) - temp * sin(laz[k]);
laz[k] = 0;
}
void modify(int k,int l,int r,int x,int y,long long c){
if(x <= l && r <= y){
double temp = stre[k];
stre[k] = stre[k] * cos(c) + ctre[k] * sin(c);
ctre[k] = ctre[k] * cos(c) - temp * sin(c);
laz[k] += c;
return;
}
push(k,l,r);
if(x <= mid) modify(k << 1,l,mid,x,y,c);
if(y > mid) modify(k << 1 | 1,mid + 1,r,x,y,c);
stre[k] = stre[k << 1] + stre[k << 1 | 1];
ctre[k] = ctre[k << 1] + ctre[k << 1 | 1];
}
double query(int k,int l,int r,int x,int y){
double ret = 0;
if(x <= l && r <= y) return stre[k];
push(k,l,r);
if(x <= mid) ret += query(k << 1,l,mid,x,y);
if(y > mid) ret += query(k << 1 | 1,mid + 1,r,x,y);
stre[k] = stre[k << 1] + stre[k << 1 | 1];
ctre[k] = ctre[k << 1] + ctre[k << 1 | 1];
return ret;
}
}STr;
int main(){
int m,n,i,j,k,x,y;
long long w;
scanf("%d",&n);
for(i = 1;i <= n;i++) scanf("%lf",&a[i]);
STr.build(1,1,n);
scanf("%d",&m);
for(i = 1;i <= m;i++){
scanf("%d",&k);
if(k == 1){
scanf("%d %d %lld",&x,&y,&w);
STr.modify(1,1,n,x,y,w);
}
if(k == 2){
scanf("%d %d",&x,&y);
printf("%.1lf\n",STr.query(1,1,n,x,y));
}
}
return 0;
}
One of the most important enlightenment we get from this question is that when we need to maintain multiple information, we must pay attention to whether we are the information before updating, so we should pay attention to the order of updating, especially when we are lazy to mark the update.
By the way, sometimes interval modification is different from single point modification, so when updating the lazy flag, it is recommended to push it first, and then write the code with the formula. This will be more obvious in the next question.
T7 variance (Luogu P1471, difficulty 3.5)
Interval addition, interval average, interval variance.
The basic content is the same. Maintain intervals and, and mark intervals.
Average number: first of all, we should make it clear that the average number in this place cannot be taken as an average of several numbers as before gcd, and then take an average of the average number obtained. In this way, the average number obtained is not an average at all. So the average can't be maintained.
At the same time, we should not only consider that the average cannot be maintained, but also realize that the average should not appear in the whole process of operation on our line segment tree, otherwise it is no different from taking the average. Therefore, the line segment tree only needs to process the sum and find the average in the main function.
Variance involves the derivation of a formula. The specific process will not be explained (not written in the Markdown editor). In short, the final conclusion is: variance = sum of squares / n + mean * mean. According to this formula, we have to maintain not only the sum of intervals, but also the sum of squares of intervals (first square and then sum, so of course it can be maintained).
How to update the sum of squares of intervals? Let's start the derivation. Let the original sum of interval squares be tre2[k], and the sum of interval squares be tre[k], then tre2[k] += 2 * tre[k] + n * tre[k] * tre[k] (n is the interval length) when updating. Here we notice that the sum of squares is used to update the sum of squares, so we should update the sum of squares first and then the sum of squares.
There is also a small problem: if you really maintain the average in the tree, do you want to maintain the length of the interval? The answer is no, because the interval length does not change in the whole process. When we need to maintain and query, l, R and mid are all given. There is no need to preprocess and take up additional space.
The code is as follows:
#include<cstdio>
#include<cstring>
#include<algorithm>
#include<cmath>
using namespace std;
#define mid (l + r >> 1)
#define X (y - x + 1)
double a[100001],tre[400001],tre2[400001],laz[400001];
struct yjx{
void build(int k,int l,int r){
if(l == r){
tre[k] = a[l];
tre2[k] = a[l] * a[l];
return;
}
build(k << 1,l,mid);
build(k << 1 | 1,mid + 1,r);
tre[k] = tre[k << 1] + tre[k << 1 | 1];
tre2[k] = tre2[k << 1] + tre2[k << 1 | 1];
}
void push(int k,int l,int r){
laz[k << 1] += laz[k],laz[k << 1 | 1] += laz[k];
tre2[k << 1] += 2 * laz[k] * tre[k << 1] + (mid - l + 1) * laz[k] * laz[k];
tre2[k << 1 | 1] += 2 * laz[k] * tre[k << 1 | 1] + (r - mid) * laz[k] * laz[k];
tre[k << 1] += laz[k] * (mid - l + 1);
tre[k << 1 | 1] += laz[k] * (r - mid);
laz[k] = 0;
}
void modify(int k,int l,int r,int x,int y,double c){
if(x <= l && r <= y){
laz[k] += c;
tre2[k] += 2 * c * tre[k] + (r - l + 1) * c * c;
tre[k] += (r - l + 1) * c;
return;
}
push(k,l,r);
if(x <= mid) modify(k << 1,l,mid,x,y,c);
if(y > mid) modify(k << 1 | 1,mid + 1,r,x,y,c);
tre[k] = tre[k << 1] + tre[k << 1 | 1];
tre2[k] = tre2[k << 1] + tre2[k << 1 | 1];
}
double aquery(int k,int l,int r,int x,int y){
if(x <= l && r <= y) return tre[k];
double ret = 0;
push(k,l,r);
if(x <= mid) ret += aquery(k << 1,l,mid,x,y);
if(y > mid) ret += aquery(k << 1 | 1,mid + 1,r,x,y);
return ret;
}
double query2(int k,int l,int r,int x,int y){
if(x <= l && r <= y) return tre2[k];
double ret = 0;
push(k,l,r);
if(x <= mid) ret += query2(k << 1,l,mid,x,y);
if(y > mid) ret += query2(k << 1 | 1,mid + 1,r,x,y);
return ret;
}
}STr;
int main(){
int i,m,n,x,y,z;
double w;
scanf("%d %d",&n,&m);
for(i = 1;i <= n;i++) scanf("%lf",&a[i]);
STr.build(1,1,n);
for(i = 1;i <= m;i++){
scanf("%d",&z);
if(z == 1){
scanf("%d %d %lf",&x,&y,&w);
STr.modify(1,1,n,x,y,w);
}
if(z == 2){
scanf("%d %d",&x,&y);
printf("%.4lf\n",STr.aquery(1,1,n,x,y) / X);
}
if(z == 3){
scanf("%d %d",&x,&y);
printf("%.4lf\n",STr.query2(1,1,n,x,y) / X - STr.aquery(1,1,n,x,y) / X * STr.aquery(1,1,n,x,y) / X);
}
}
return 0;
}
The Enlightenment of this question is that the information that cannot be merged and maintained in the line segment tree is best not to appear in the line segment tree, and the information not updated in the line segment tree does not need to be maintained through the line segment tree.
2 continuity issues
All the above mentioned are to maintain a value. For continuity problems, we should care about the value of a section. The updating and maintenance of this problem will be more complex.
T8 Xiaobai Park (Luogu P4513, difficulty 4)
Maximum sub segment sum of interval, single point modification.
Single point modification, no lazy mark is required. It is maintained when it is modified, and no other optimization is available.
The problem with this problem is how to maintain a continuous sub segment during recursion. At this time, we can't just add it as before.
It is better to maintain the largest sub segment from the left and right sub segments, that is, to maintain the largest sub segment from the left and right sub segments.
lrs is obviously the simplest. Add the left and right sons together.
There may be three kinds of sections for the largest son, left and right, ls and son.
For mx, the first is the above three, and the second may be the sum of the largest sub segment from the right of the left son, the sum of the largest sub segment from the left of the right son and the sum of these two segments.
Note: Here we discuss how to merge, so we should merge first and then discuss, that is, use the updated information.
In the code, it should be like this:
z.lrs = x.lrs + y.lrs; z.ls = max(z.lrs,max(x.ls,max(x.lrs,x.lrs + y.ls))); z.rs = max(z.lrs,max(y.rs,max(y.lrs,y.lrs + x.rs))); z.mx = max(x.mx,max(y.mx,max(x.rs + y.ls,max(z.ls,max(z.rs,z.lrs)))));
I really don't know how to simplify some cases that I won't get. Please share with dalao who has ideas in the comment area.
In addition, it should be noted that there are similar merging operations during query. This operation also needs to be carried out as above. This is why we use structures instead of arrays as before. In addition, this kind of merging operation is only necessary when the query interval is not covered by the target interval and just exceeds the target interval on the left and right. Therefore, it is necessary to refine the classification discussion of the query.
The code is as follows:
#include<cstdio>
#include<cstring>
#include<algorithm>
using namespace std;
#define mid (l + r >> 1)
int a[500001];
struct wyx{
long long ls,rs,lrs,mx;
}tre[2000001];
struct yjx{
wyx update(wyx x,wyx y){
wyx z;
z.lrs = x.lrs + y.lrs;
z.ls = max(z.lrs,max(x.ls,max(x.lrs,x.lrs + y.ls)));
z.rs = max(z.lrs,max(y.rs,max(y.lrs,y.lrs + x.rs)));
z.mx = max(x.mx,max(y.mx,max(x.rs + y.ls,max(z.ls,max(z.rs,z.lrs)))));
return z;
}
void build(int k,int l,int r){
if(l == r){
tre[k].ls = tre[k].rs = tre[k].lrs = tre[k].mx = a[l];
return;
}
build(k << 1,l,mid);
build(k << 1 | 1,mid + 1,r);
tre[k] = update(tre[k << 1],tre[k << 1 | 1]);
}
void modify(int k,int l,int r,int x,int c){
if(l == r){
tre[k].ls = tre[k].rs = tre[k].lrs = tre[k].mx = c;
return;
}
if(x <= mid) modify(k << 1,l,mid,x,c);
else modify(k << 1 | 1,mid + 1,r,x,c);
tre[k] = update(tre[k << 1],tre[k << 1 | 1]);
}
wyx query(int k,int l,int r,int x,int y){
// printf("%d %d %lld?\n",l,r,mx[k]);
if(x <= l && r <= y) return tre[k];
if(y <= mid) return query(k << 1,l,mid,x,y);
if(x > mid) return query(k << 1 | 1,mid + 1,r,x,y);
if(x <= mid && y > mid) return update(query(k << 1,l,mid,x,y),query(k << 1 | 1,mid + 1,r,x,y));
}
}STr;
int main(){
//freopen("Segtree.in","r",stdin);
//freopen("Segtree.out","w",stdout);
int i,m,n,w,x,y,z;
memset(tre,-0x3f,sizeof(tre));
scanf("%d %d",&n,&m);
for(i = 1;i <= n;i++) scanf("%d",&a[i]);
STr.build(1,1,n);
for(i = 1;i <= m;i++){
scanf("%d",&z);
if(z == 2){
scanf("%d %d",&x,&w);
STr.modify(1,1,n,x,w);
}
if(z == 1){
scanf("%d %d",&x,&y);
if(x > y) swap(x,y);
printf("%lld\n",STr.query(1,1,n,x,y).mx);
}
}
return 0;
}
In general, the key to this sub segment problem is to take into account the changes of merging operation. Therefore, the order of inquiry and update is different from that of the previous problems, and the application of structure is also different from that of the previous problems. At the same time, it is naturally more complex than those above.
III. summary
The line segment tree problem is a huge problem, and what we introduce here is only a very basic application (which is why it can only be "up"). For this part of basic applications, the following aspects can be considered:
1 Optimization (for example, whether to mark lazy and when to avoid operation)
2. Maintenance objects (whether they can be maintained, how to maintain them, and how to deal with the initial tree creation)
3. Update operation (update sequence, merging method and lazy tag processing)
In addition, we must avoid low-level errors. The bug of line segment tree is too difficult to find (cover your face).
"This should not be wrong."
For example, someone debug s an MLE question for an hour and finds that it is because mid+1 and r are written backwards during recursion
Thank you for reading!