catalogue
Quick drainage by pit excavation method
Left and right pointer fast row
Non recursive code implementation
Sorting concept
Sorting: the so-called sorting is the operation of arranging a string of records incrementally or decrementally according to the size of one or some keywords.
Stability: if there are multiple records with the same keyword in the record sequence to be sorted, the relative order of these records remains unchanged after sorting, that is, in the original sequence, r[i]=r[j], and r[i] is before r[j], while in the sorted sequence, r[i] is still before r[j], then this sorting algorithm is said to be stable; Otherwise, it is called unstable.

Common sorting:
Insert sort
Direct insertion sort is a simple insertion sort method. Its basic idea is to insert the records to be sorted into an ordered sequence one by one according to the size of their key values, until all records are inserted, and a new ordered sequence is obtained.
Let's assume that the first digit is in order. When inserting the I (I > = 1) th element, the preceding array[0],array[1],..., array[i-1] are already in order. At this time, compare the sorting code of array[i] with that of array[i-1],array[i-2],... To find the insertion position, that is, insert array[i], and move the elements in the original position backward.
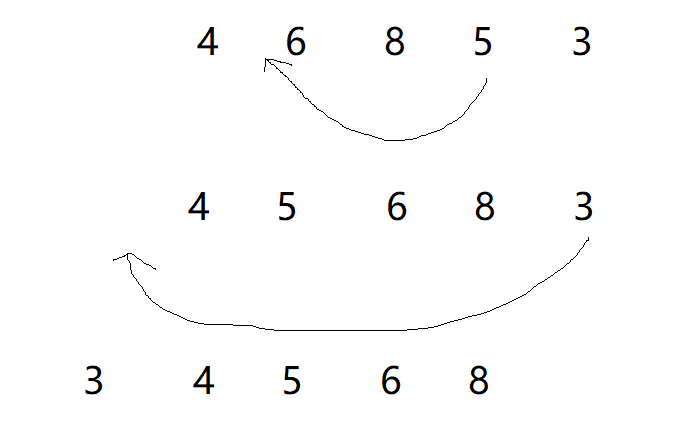
There are two cases of insertion, that is, the inserted data is in the middle and in the front.
When we insert the last element, the first n-1 elements are already in order.
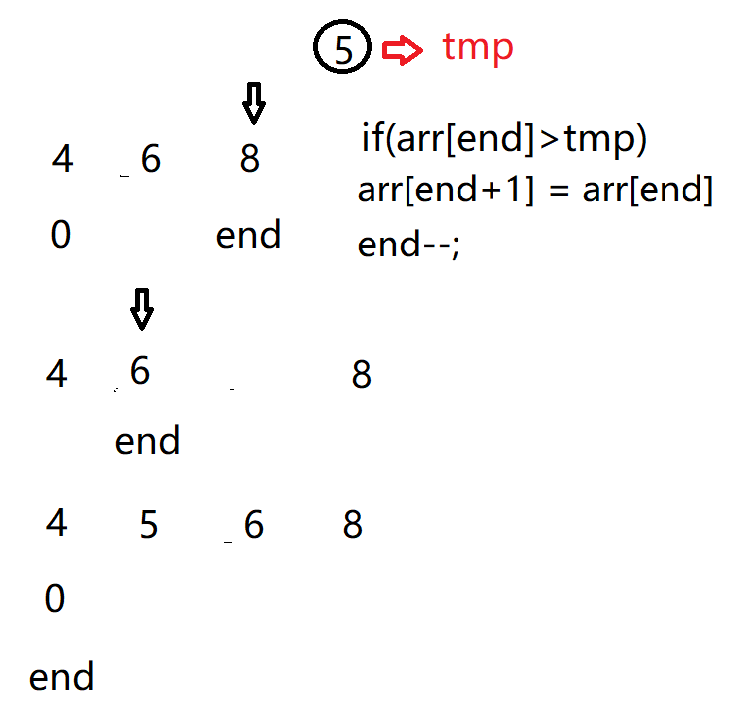
Code implementation:
class InsertSort{
public static void InsertSort(int []arr) {
for (int i = 0; i < arr.length - 1; i++) {
int end = i;
int tmp = arr[end + 1];
while (end >= 0) {
if (arr[end] > tmp) {
arr[end + 1] = arr[end];
end--;
} else {
break;
}
}
arr[end + 1] = tmp;
}
System.out.println(Arrays.toString(arr));
}
}
public class Test {
public static void main(String[] args) {
int arr[] = {10,24,5,25,39,46,43};
InsertSort.InsertSort(arr);
}
}Time complexity analysis: in the worst case, that is, in reverse order, the number of moves is 1+2+3+...+n-1, that is, the sum of the arithmetic sequence is O (n^2);
Spatial complexity analysis: O (1);
Stability: stable
Shell Sort

Hill ranking method is also known as reduced increment method. The basic idea of Hill ranking method is to select an integer (gap) first , divide all records in the file to be sorted into groups. All records with distance are divided into the same group, and sort the records in each group. Then, take and repeat the above grouping and sorting. When = 1, all records are sorted in the same group.
Hill sorting is actually an optimization of insertion sorting. When we are faced with array sorting in reverse order, we first pre sort the array through gap grouping to make the array as orderly as possible. Finally, we complete the sorting through insertion sorting.
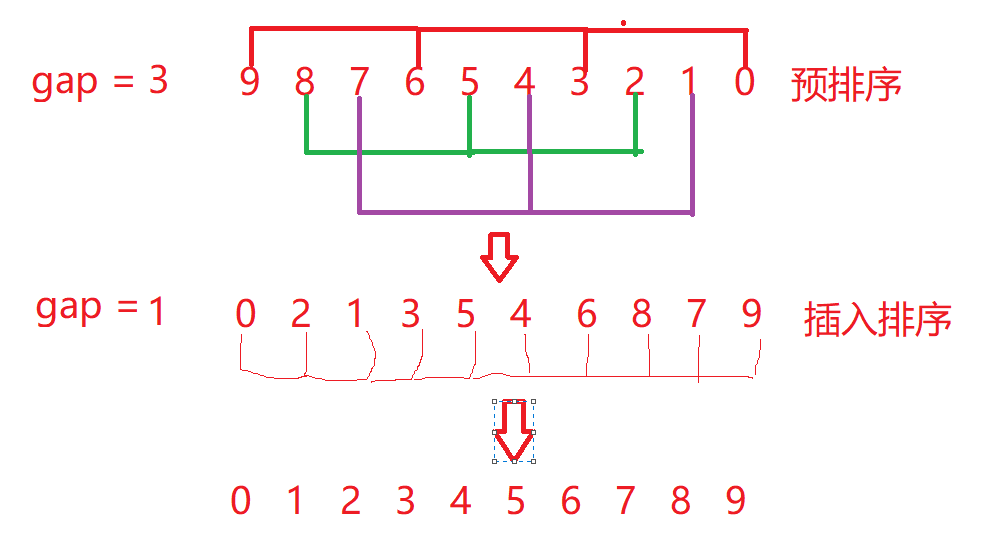
We found that pre sorting is actually several insertion sorting, but if we insert sorting separately, the efficiency will be very low, so we still carry out insertion sorting in order, but the subscript of insertion sorting is the 0,1,2 subscript of the group they have divided. How to determine which group they are? It's not good to add a gap.
end starts from 0. end+gap is a group. The divided groups are inserted and sorted.
ps: the larger the gap, the faster the sorting speed, but the smaller the gap, the closer the sorting is. Generally, we divide the gap sorted by hill by 2 every time to ensure that the gap of the last time must be equal to 1, that is, the last time must be inserted Sorting, or divide the gap by 3 and add 1 at the end to ensure that the final result of gap is 1
code implementation
class ShellSort{
public static void ShellSort(int []arr){
int gap = arr.length;
while(gap >= 1) {
gap = gap/ 2;
for (int i = 0; i < arr.length - gap;i++) {
int end = i;
int tmp = arr[end + gap];
while (end >= 0) {
if (arr[end] > tmp) {
arr[end + gap] = arr[end];
end -= gap;
} else {
break;
}
}
arr[end+gap] = tmp;
}
}
System.out.println(Arrays.toString(arr));
}
}
public class Test {
public static void main(String[] args) {
int arr1[] = {9,8,7,6,5,4,3,2,1,0};
ShellSort.ShellSort(arr1);
}
}Time complexity analysis:
In our algorithm:
When the gap is large, each number moves at least once, so the time complexity is close to O(n)

When gap is very small, the array is close to order and the number of moves is close to O (n).
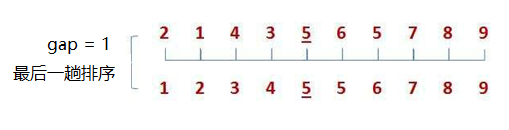
When we use gap/2, the number of times to sort x is the logarithm with base 2 and exponent n, logn.
Therefore, the overall time complexity is O (log N) * N);
However, after consulting the books, I found that the time complexity of hill sorting is O (N ^1.3). I won't go into details. Interested partners can learn about it.
Space complexity: 0 (1);
Stability: unstable
Select sort
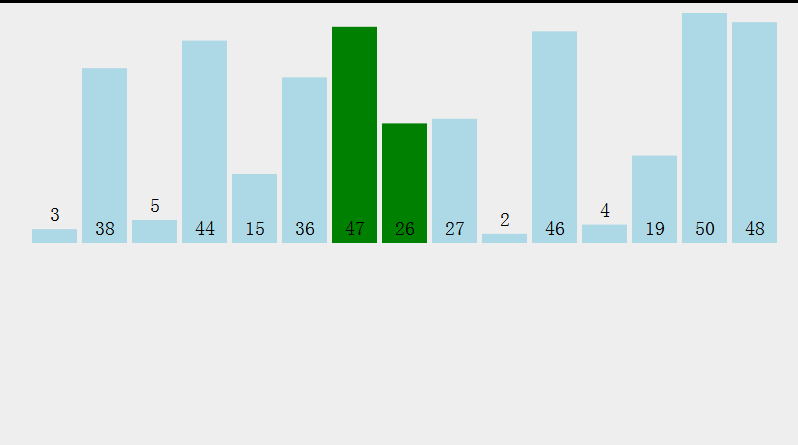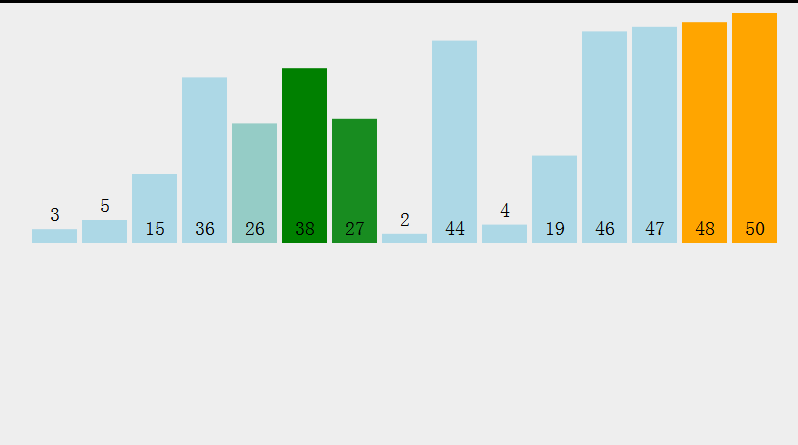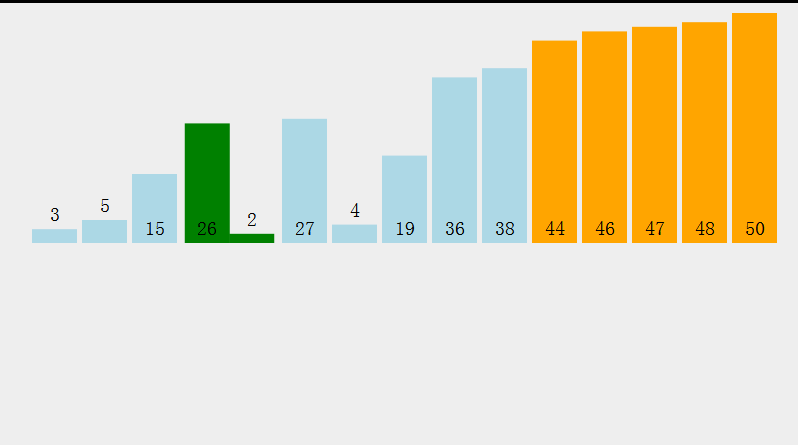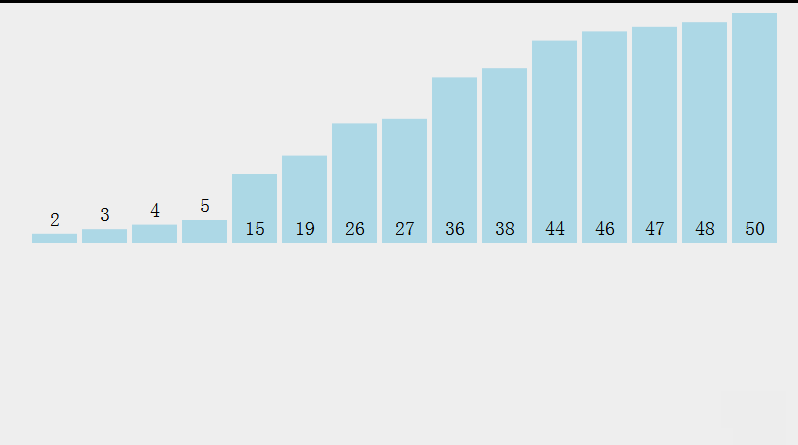
Idea: select the smallest (or largest) element from the data elements to be sorted each time and store it at the beginning of the sequence until all the data elements to be sorted are finished.
Select the data element with the largest (smallest) key in the element set array [i] - array [n-1]. If it is not the last (first) element in this group, it will be exchanged with the last (first) element in this group. In the remaining array [i] - array [n-2] (array [i + 1] - array [n-1]) set, repeat the above steps until there is 1 element left in the set.
Sorting is too simple. It's directly on the code.
code implementation
class SelectSort{
public static void SelectSort(int []arr){
for(int i = 0;i < arr.length - 1;i++){
int min = i;
for(int j = i + 1;j < arr.length ;j++){
if(arr[j] < arr[min]){
min = j;
}
}
if(min != i){
int tmp = arr[i];
arr[i] = arr[min];
arr[min] = tmp;
}
}
System.out.println(Arrays.toString(arr));
}
}Time complexity analysis: O (n^2)
It is very easy to understand the direct selection and sorting thinking, but the efficiency is not very good. It is rarely used in practice
Space complexity: O (1)
Stability: unstable
Heap sort
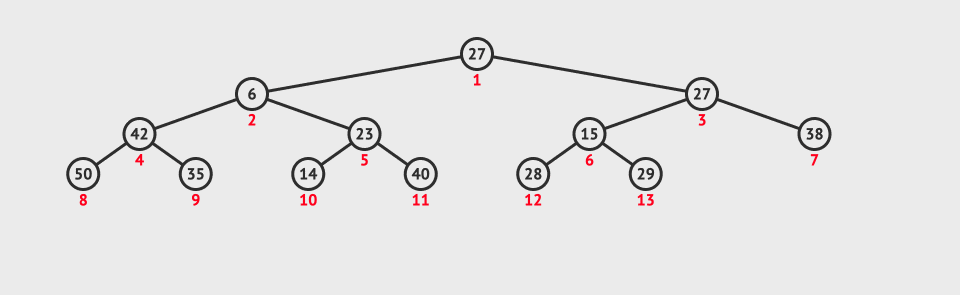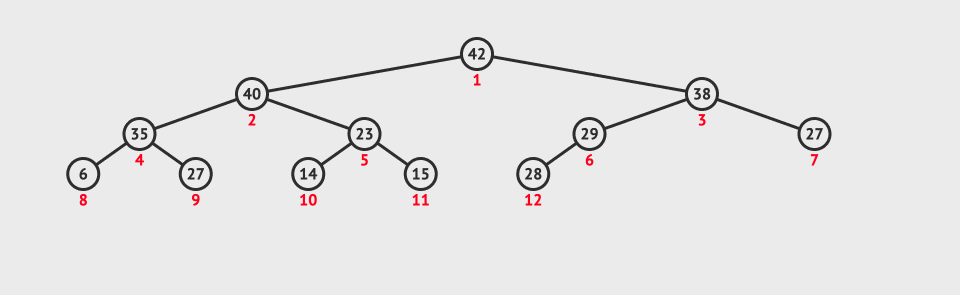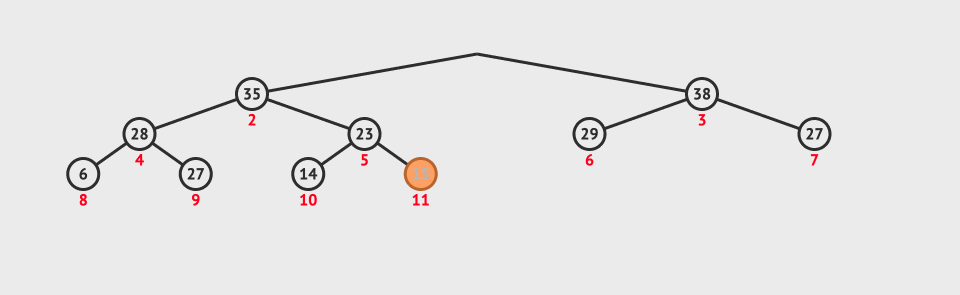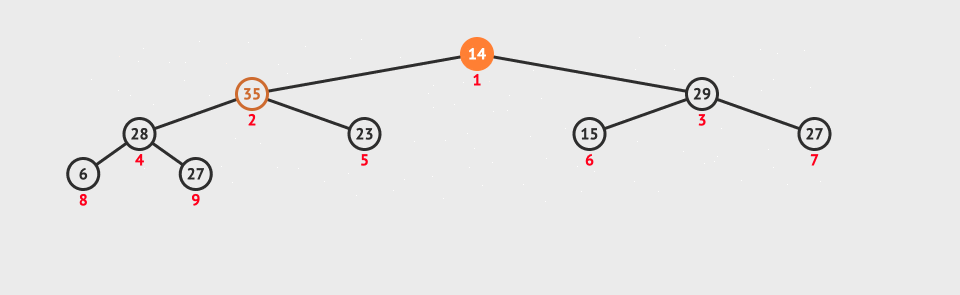
Before we know the heap sort, we need to know what a heap is.
The logical structure of the heap is a complete binary tree, and the physical structure is an array.
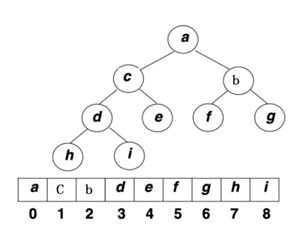
We can express the parent-child relationship through the subscript of the array:

The heap has two representation structures:
Large top heap: the parent node is larger than all child nodes - find the maximum value
Small top heap: the parent node is smaller than all child nodes - find the minimum value
So how do we sort by heap?
For heap sorting, we must build a heap first. How to sort without a heap. So the first step is to build a heap.

Given an array, we build the heap. Because the logical structure of the heap is a complete binary tree, is it easy to build the heap?
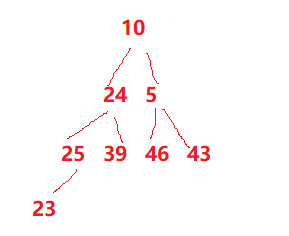
Note: This is not a heap, because there are only large top heap and small top heap, so it is very complicated to build a heap.
So we introduce a downward adjustment algorithm.
Downward adjustment algorithm:
Premise: ① ascending order: the left and right subtrees are large piles; ② descending order: the left and right subtrees are small piles.
Methods (in ascending order): starting from the root node, select a larger number from the left and right subtrees to compare with the parent node. If the child node is larger than the parent node, choose the exchange. Then, re adjust the child node as a parent node and continue to move down.
The following figure shows the adjustment in descending order:
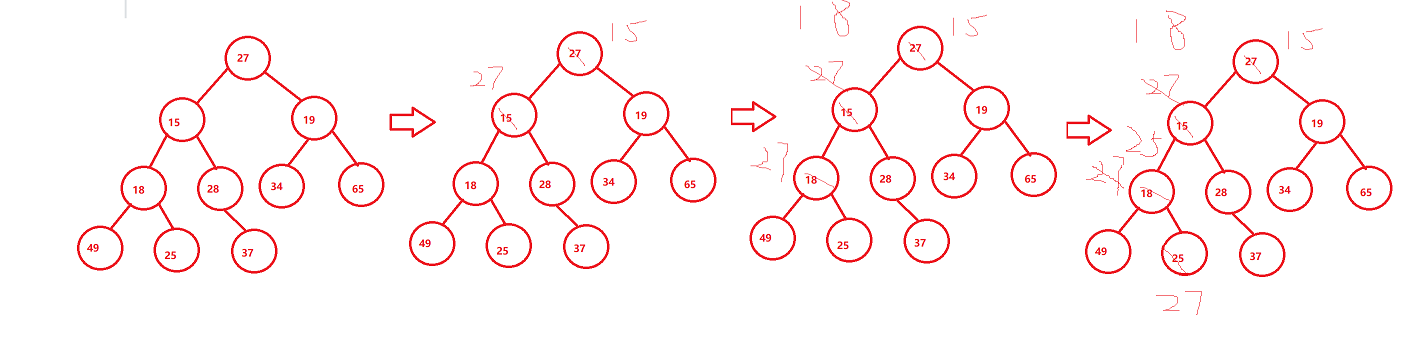
Ascending order is to find the big one, which is the opposite.
We can find the maximum and minimum value in the heap through this algorithm, but what's the use? And its premise is difficult to meet.
Then we might as well start from the bottom, adjust it downward, and then up in turn. Finally, the heap is in good order.
However, there is only one element in the last layer, so there is no significance of adjustment. Then adjust from the position of the last non leaf node. But how do you find this location? The last non leaf node is the parent node of the last leaf node. That's easy to find. Just substitute it into the formula.
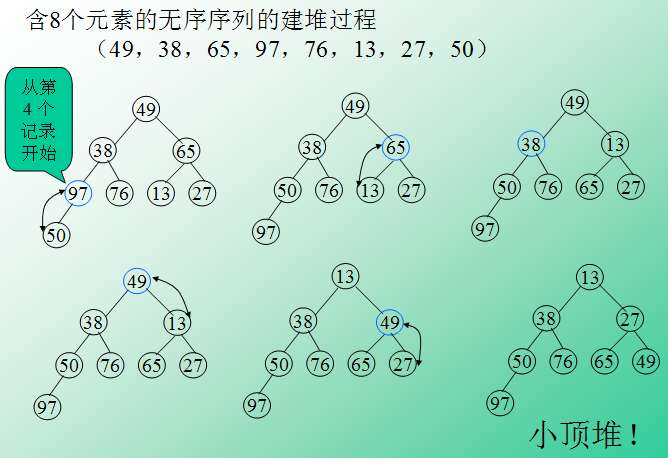
Then the code is well implemented. The figure below shows the construction of a large pile top. For a small pile top, just change the greater than to less than.

When we are sorting in ascending order, we need to build a lot, because if we build a small heap, we find the minimum value at the top of the heap, and the minimum value will be fixed and cannot move. Then we need to rebuild the heap to find a minimum value, so that the heap sorting will be inefficient.
If we build a lot, then the maximum value is at the top of the heap. We just need to exchange the elements at the top of the heap with the last element. When we readjust downward, we can reduce the length to be adjusted by one. Then we can find the next largest element, exchange it to the penultimate position, and then adjust it until the array becomes an ascending array.

Complete code
class HeapSort{
public static void AdjustDown(int []arr,int root,int length){
int parent = root;
int child = parent * 2 + 1;
while(child < length){
if(child + 1 < length && arr[child + 1] > arr[child]){
child += 1;
}else {
if(arr[child] > arr[parent]){
int tmp = arr[parent];
arr[parent] = arr[child];
arr[child] = tmp;
parent = child;
child = parent * 2 + 1;
}else {
break;
}
}
}
}
public static void HeapSort(int []arr){
for(int i = (arr.length - 1 - 1) / 2;i >= 0;i--){//Build pile
HeapSort.AdjustDown(arr,i,arr.length);
}
int length = arr.length -1;
while(length > 0){
int tmp = arr[0];
arr[0] = arr[length];
arr[length] = tmp;
HeapSort.AdjustDown(arr,0,length);
length --;
}
System.out.println(Arrays.toString(arr));
}
}Time complexity analysis:
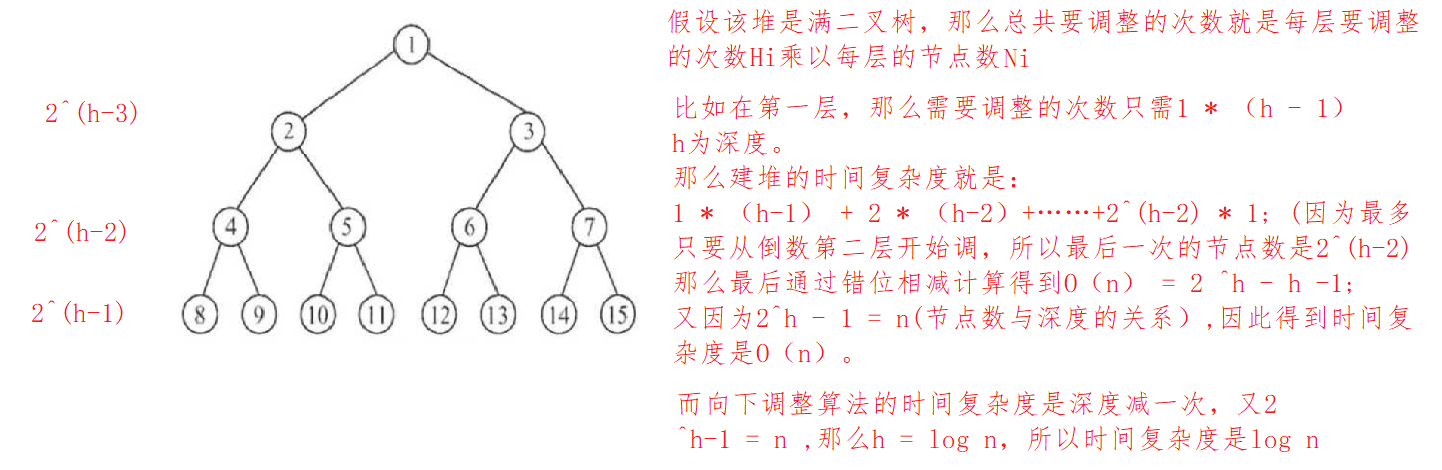
Therefore, the overall time complexity is the most frequent: the heap sort is adjusted downward, that is, O(N * log N)
Spatial complexity: O (1);
Stability: unstable
Bubble sorting

Bubble sorting is also easy to understand. Compare the previous number with the next number, move the large one back until the end, and then the small element will slowly float to the top of the array, so it is called bubble sorting.
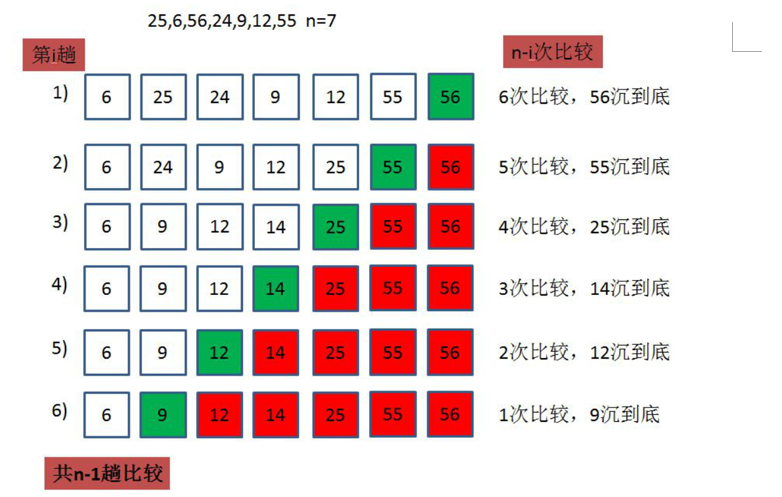
code implementation
class BubbleSort{
public static void BubbleSort(int []arr){
for(int i = 0;i < arr.length;i++){
for(int j = 1;j < arr.length - i;j++){
if(arr[j-1] > arr[j]){
int tmp = arr[j-1];
arr[j-1] = arr[j];
arr[j] = tmp;
}
}
}
System.out.println(Arrays.toString(arr));
}
}Time complexity analysis: n-1 times need to be sorted, which are n, n-1,n-2... 1
The total number of times is n(n-1)/2, i.e. O (n^2)
Spatial complexity: O (1);
Stability: stable
Quick sort
Quick sort is an exchange sort method of binary tree structure proposed by Hoare in 1962. Its basic idea is: any element in the element sequence to be sorted is taken as the reference value, and the set to be sorted is divided into two subsequences according to the sort code. All elements in the left subsequence are less than the reference value, and all elements in the right subsequence are greater than the reference value, Then the leftmost and leftmost subsequences repeat the process until all elements are arranged in the corresponding positions.
There are many ways to implement quick sort
The first method: excavation method
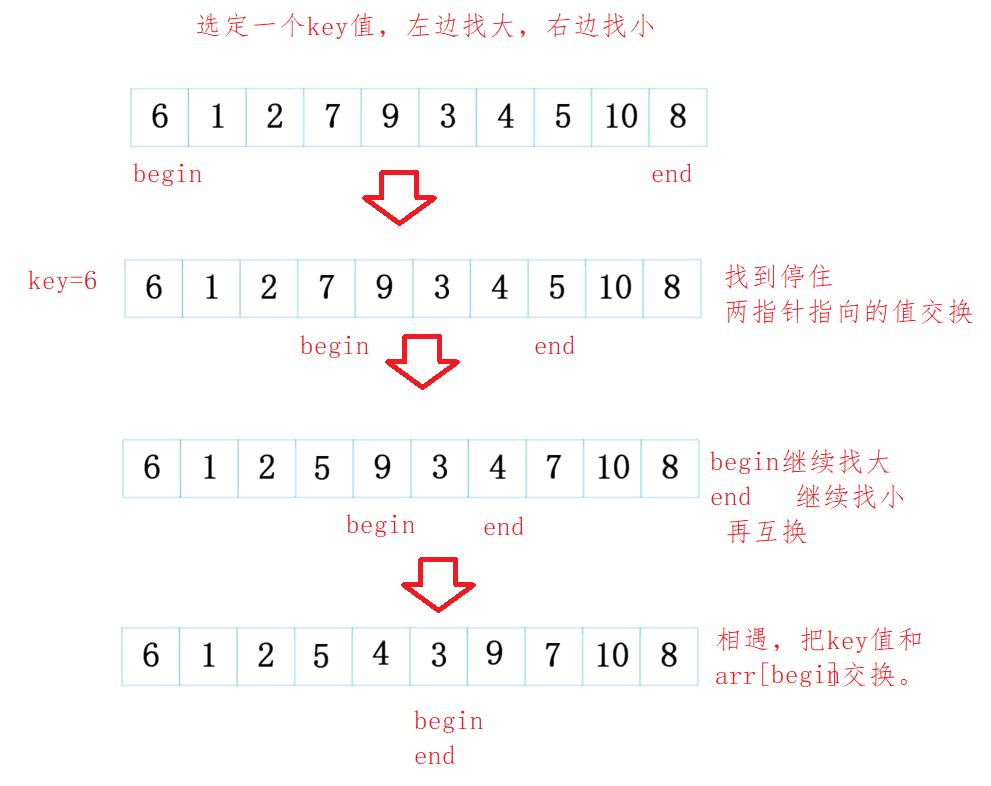
Quick drainage by pit excavation method
Given an array.
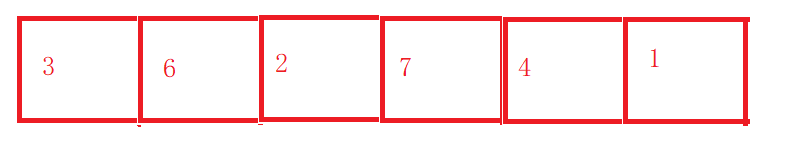
We select a position at the leftmost or rightmost as the pit. Assign the value of the pit position to a key. If the pit is on the left, find the element with smaller key from the right. If the pit is on the right, find the element with larger key from the left. When it is found, the position of the pit is regarded as a new pit, and the value of the element is assigned to the original pit position.
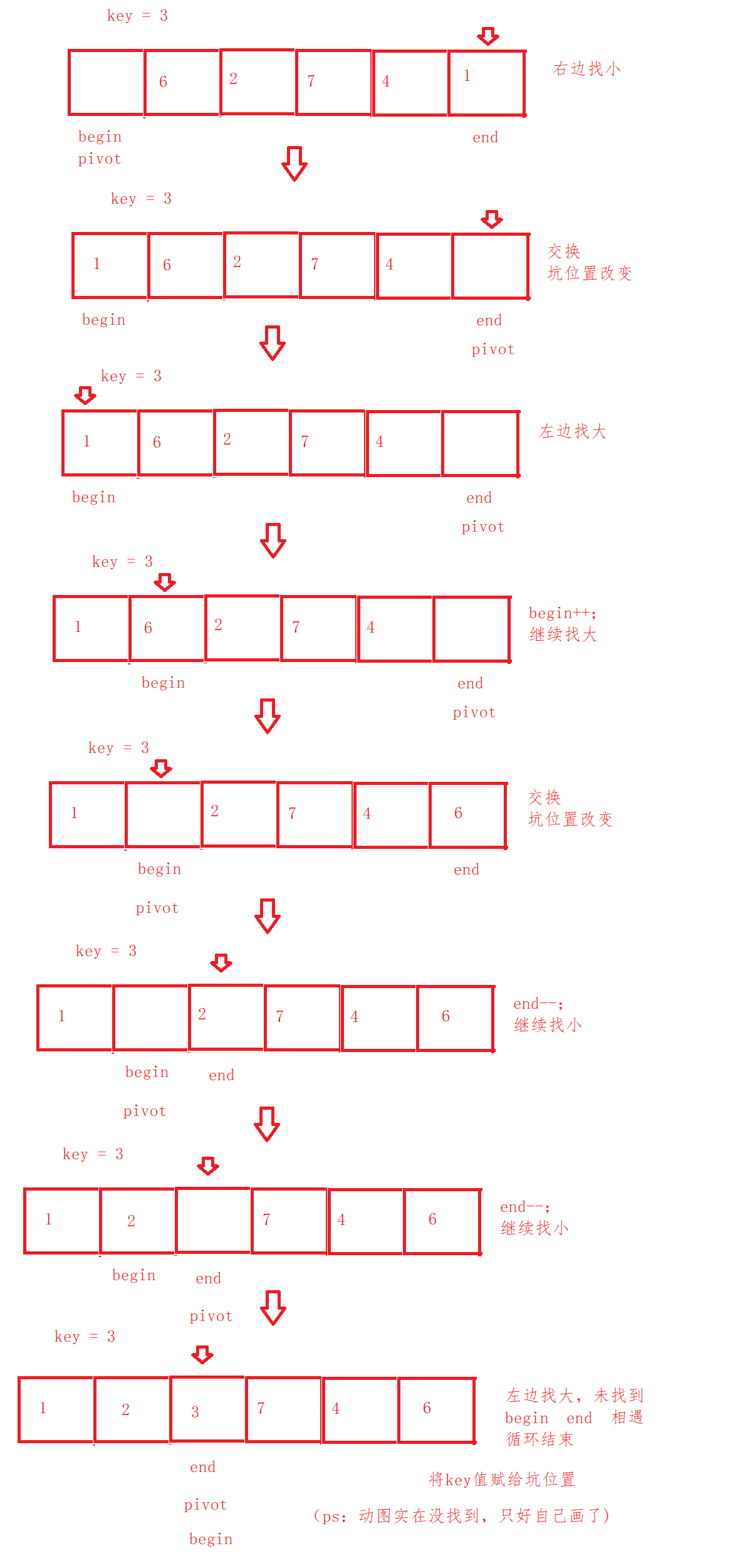
Through the pit digging method, we divide the values greater than and less than key into the left and right sides of the pit, so the values of the pit position are in good order. We just need to re sort the values on the left and right sides of the pit. How? Recursion is good. The elements on the left will be sorted again, and the elements on the right will be sorted again. Until only one element is divided into the left and right sides, the elements will be sorted.

Recursive code implementation
class QuickSort1{//Excavation method
public static void QuickSort(int []arr,int left,int right){
if(left >= right){
return;
}
int begin = left;
int end = right;
int pivot = begin;
int key = arr[begin];
while(begin < end){
while(begin < end && arr[end] >= key){
end --;
}
arr[pivot] = arr[end];
pivot = end;
while (begin < end && arr[begin] <= key){
begin++;
}
arr[pivot] = arr[begin];
pivot = begin;
}
pivot = begin;
arr[pivot] = key;
QuickSort(arr,left,pivot-1);
QuickSort(arr,pivot+1,right);
}
}Time complexity analysis:
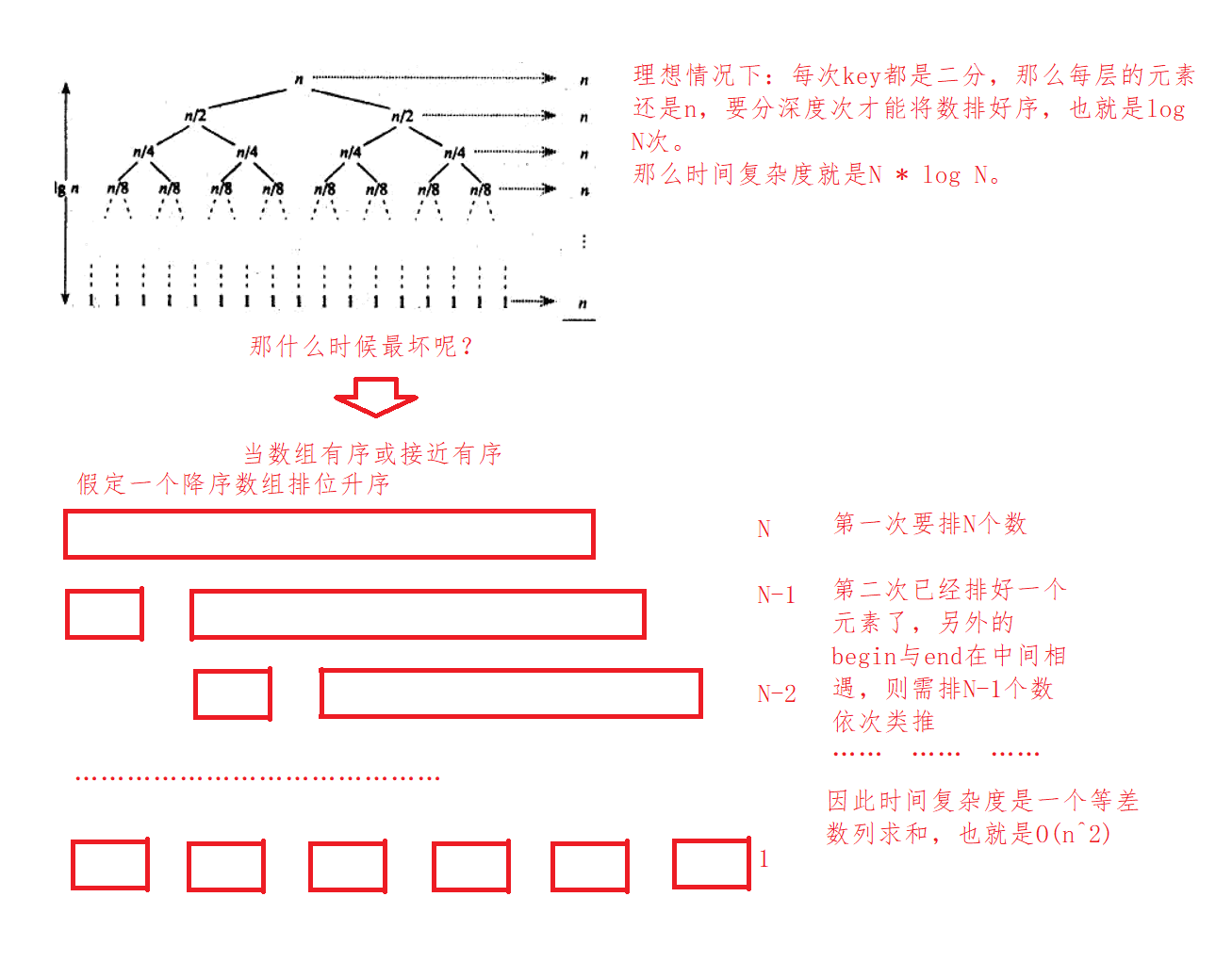
expand:
Optimization of excavation method ①: three data acquisition
Triple digit centring: because when the array is close to order, the time complexity of fast scheduling reaches O (n^2). In order to prevent this situation, someone thought of a wonderful method. In triple digit centring, in the array interval of a given partition, take the subscript of mid as the sum of left interval and right interval divided by 2, and then take the number that is not the largest or the smallest from the three numbers as the key, Then divide it down.
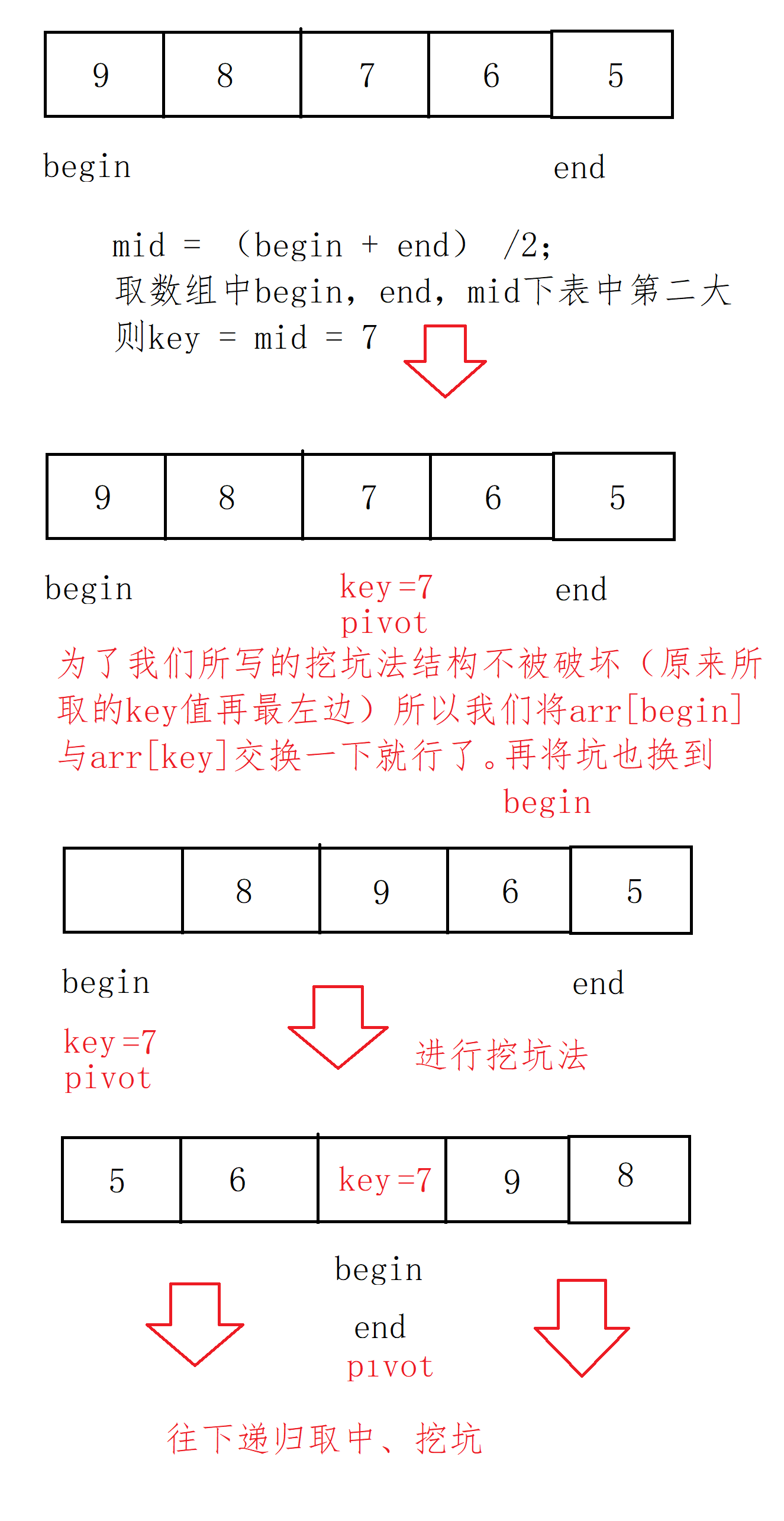
Code implementation:
class QuickSort2{//Three data acquisition by pit excavation method
public static void Swap(int []arr,int x,int y){
int tmp = arr[x];
arr[x] = arr[y];
arr[y] = tmp;
}
public static int midIndex(int []arr,int i,int j){
int mid = (i + j) / 2;
if(arr[i] < arr[mid]){
if(arr[mid] < arr[j]){
return mid;
}else if(arr[i] > arr[j]){
return i;
}else{
return j;
}
}else{
if(arr[j] < arr[mid]){
return mid;
}else if(arr[j] > arr[i]){
return i;
}else{
return j;
}
}
}
public static void quickSort(int []arr,int left,int right){
if(left >= right){
return;
}
int Index = midIndex(arr,left,right);
int begin = left;
int end = right;
Swap(arr,begin,Index);
int pivot = begin;
int key = arr[begin];
while(begin < end){
while(begin < end && arr[end] >= key){
end --;
}
arr[pivot] = arr[end];
pivot = end;
while (begin < end && arr[begin] <= key){
begin++;
}
arr[pivot] = arr[begin];
pivot = begin;
}
pivot = begin;
arr[pivot] = key;
quickSort(arr,left,pivot-1);
quickSort(arr,pivot+1,right);
}
}Pit excavation optimization ②: inter district optimization
Inter cell Optimization: however, when there is a large amount of data, the lower layers occupy too many recursion times and waste efficiency. Although these are nothing to the cpu, we still hope to optimize the algorithm.
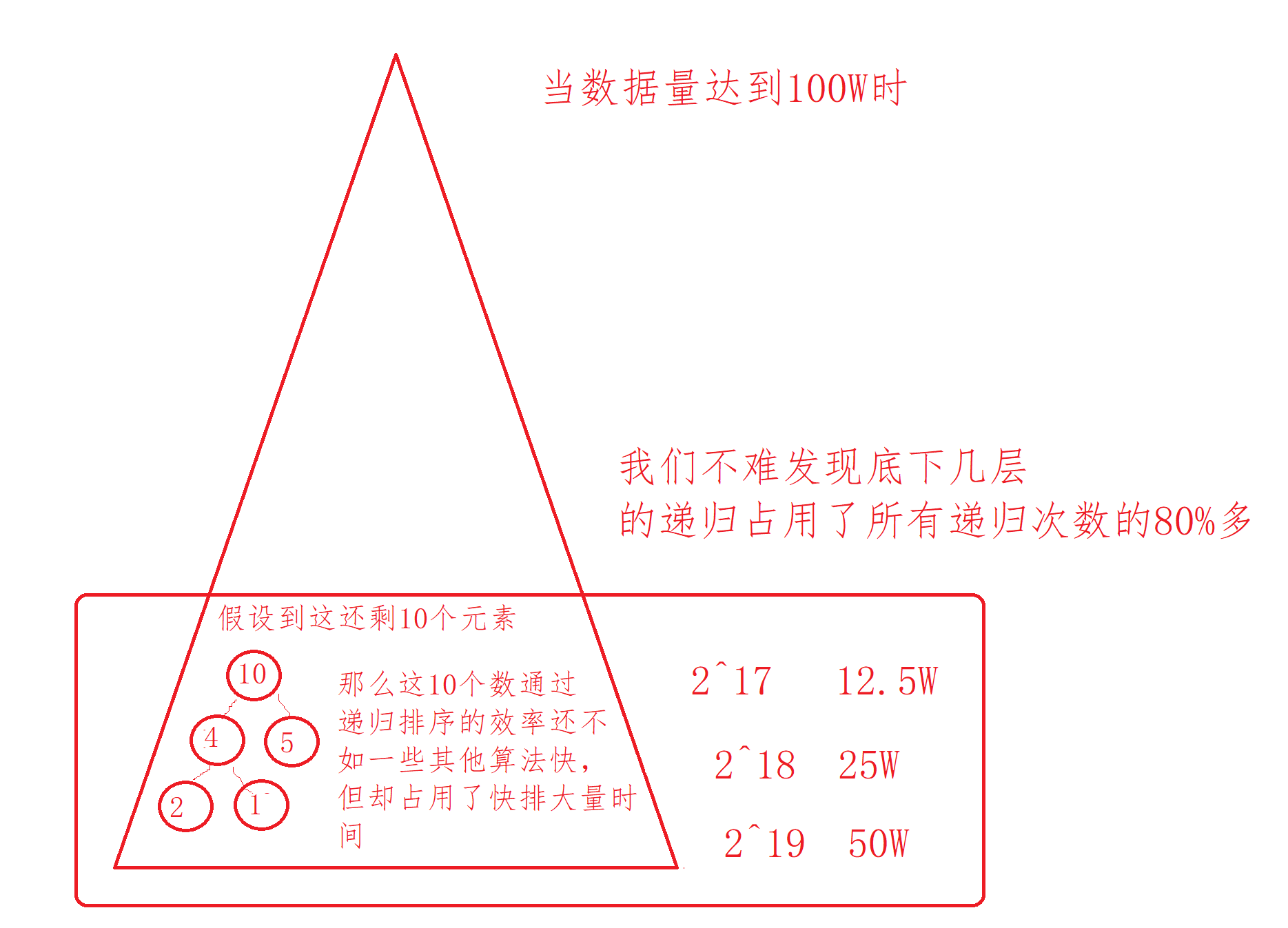
Then we might as well use other sorting instead of recursion when the length of the left and right intervals is less than 10. If it is greater than 10, let it continue recursion, then the algorithm can be optimized again. So which sort? We recommend using insert sort, because it is not suitable except that insert sort can row faster in smaller data. Hill has to go through pre sort and build heap, let alone bubbling and selection. So we use insert sort.
code implementation
class QuickSort3{
public static void Swap(int []arr,int x,int y){
int tmp = arr[x];
arr[x] = arr[y];
arr[y] = tmp;
}
public static void InsertSort(int []arr,int left,int right) {//The insertion sort is deformed
for (int i = left; i < right; i++) {
int end = i;
int tmp = arr[end + 1];
while (end >= 0) {
if (arr[end] > tmp) {
arr[end + 1] = arr[end];
end--;
} else {
break;
}
}
arr[end + 1] = tmp;
}
}
public static int midIndex(int []arr,int i,int j){
int mid = (i + j) / 2;
if(arr[i] < arr[mid]){
if(arr[mid] < arr[j]){
return mid;
}else if(arr[i] > arr[j]){
return i;
}else{
return j;
}
}else{
if(arr[j] < arr[mid]){
return mid;
}else if(arr[j] > arr[i]){
return i;
}else{
return j;
}
}
}
public static void quickSort3(int []arr,int left,int right){
if(left >= right){
return;
}
int Index = midIndex(arr,left,right);
int begin = left;
int end = right;
Swap(arr,begin,Index);
int pivot = begin;
int key = arr[begin];
while(begin < end){
while(begin < end && arr[end] >= key){
end --;
}
arr[pivot] = arr[end];
pivot = end;
while (begin < end && arr[begin] <= key){
begin++;
}
arr[pivot] = arr[begin];
pivot = begin;
}
pivot = begin;
arr[pivot] = key;
if(pivot - 1 - left > 10){
quickSort3(arr,left,pivot-1);
}else {//Insert sorting when all elements in the left interval are less than 10
InsertSort(arr,left,pivot - 1);
}
if(right - pivot - 1 >10) {
quickSort3(arr, pivot + 1, right);
}else{//Insert sorting when all elements in the right interval are less than 10
InsertSort(arr,pivot + 1,right);
}
}
}Left and right pointer fast row
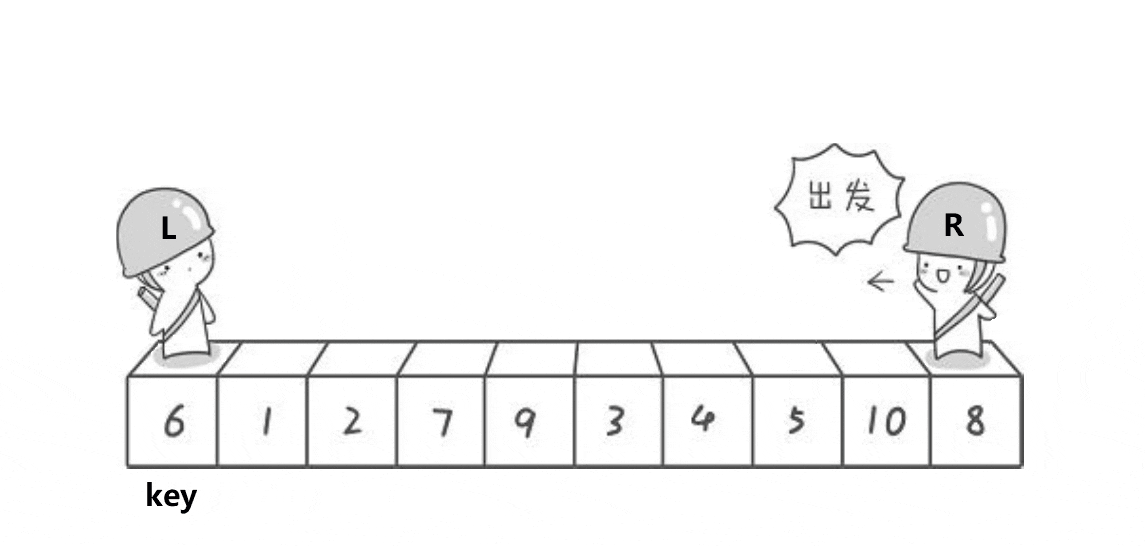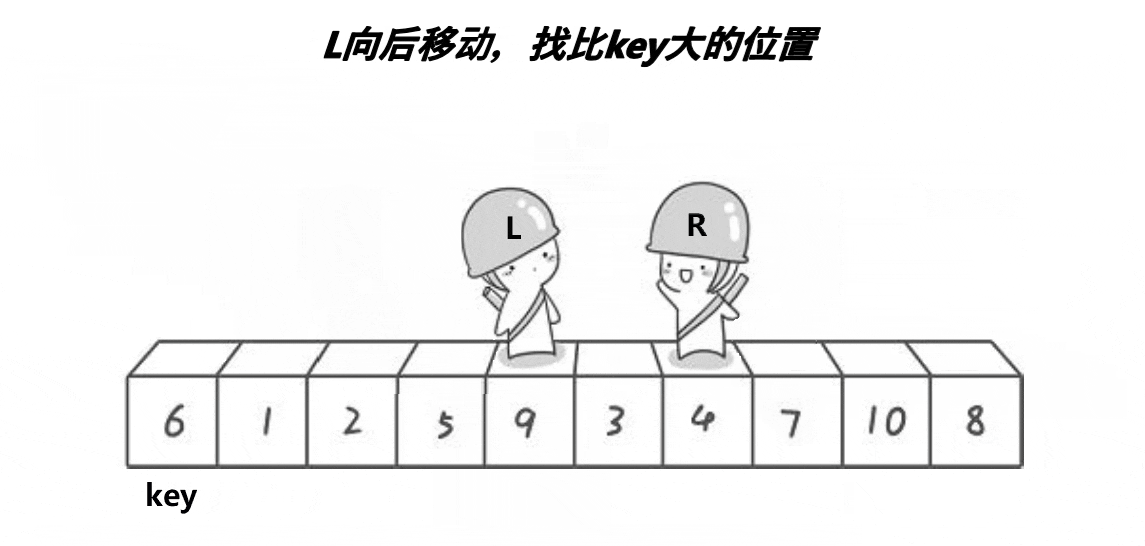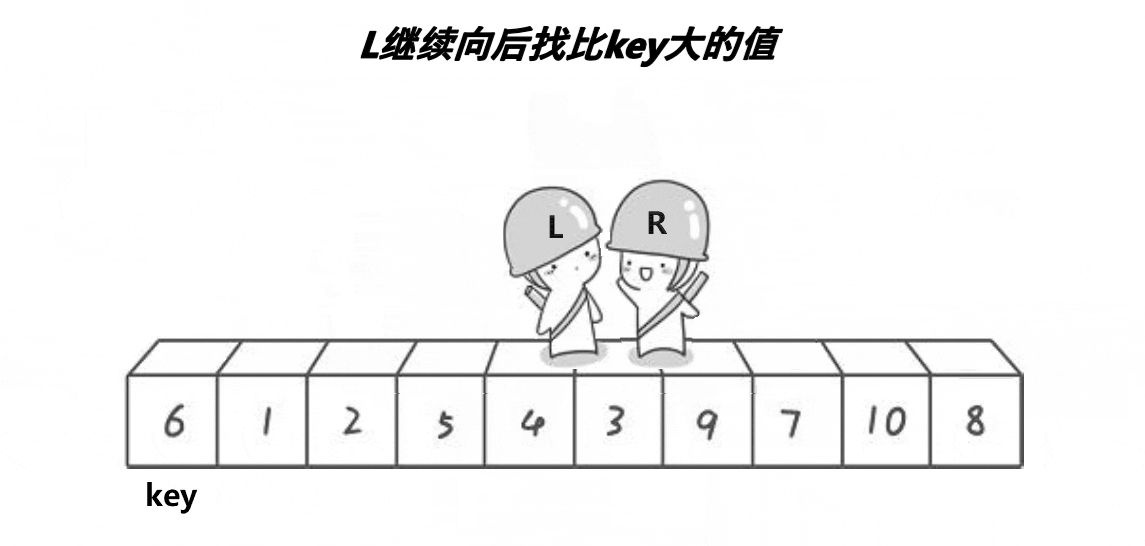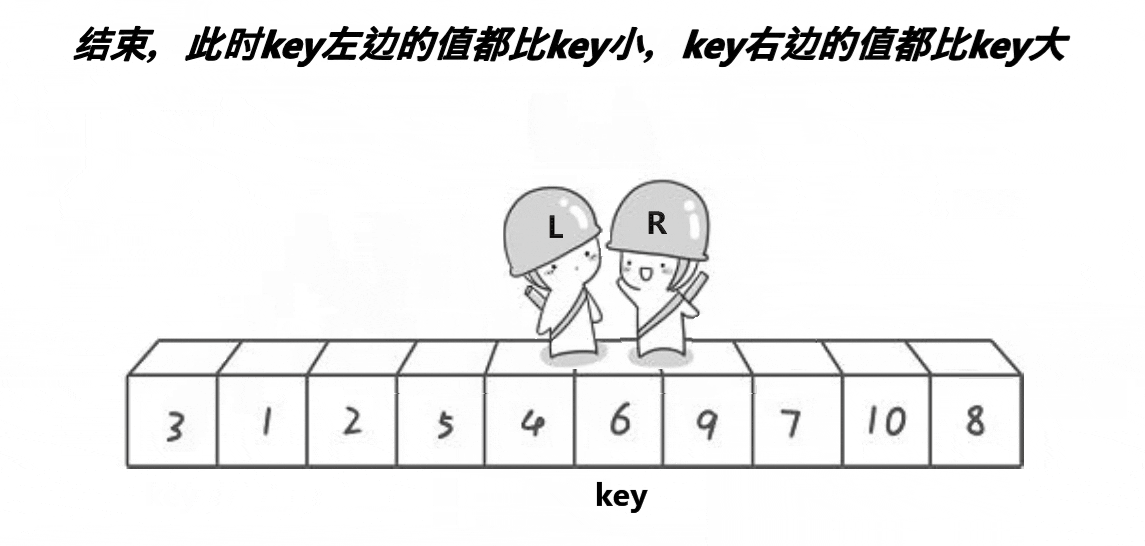
Similar to the pit digging method, but in different forms, the written functions can be found in the pit digging method.
code implementation
public static void partSort(int []arr,int left,int right){
if(left >= right){
return;
}
int Index = midIndex(arr,left,right);
Swap(arr,left,Index);
int begin = left;
int end = right;
int key = begin;
while(begin < end){
while(begin < end && arr[end] >= arr[key]){//Find small
end--;
}
while(begin < end && arr[begin] <= arr[key]){//Find big
begin++;
}
Swap(arr,begin,end);
}
Swap(arr,begin,key);
partSort(arr,left,begin-1);
partSort(arr,begin+1,right);
}Front and back pointer method
In fact, the ideas are the same, but the way of sorting is different at one time. Each subsequent sorting is divide and conquer recursion.
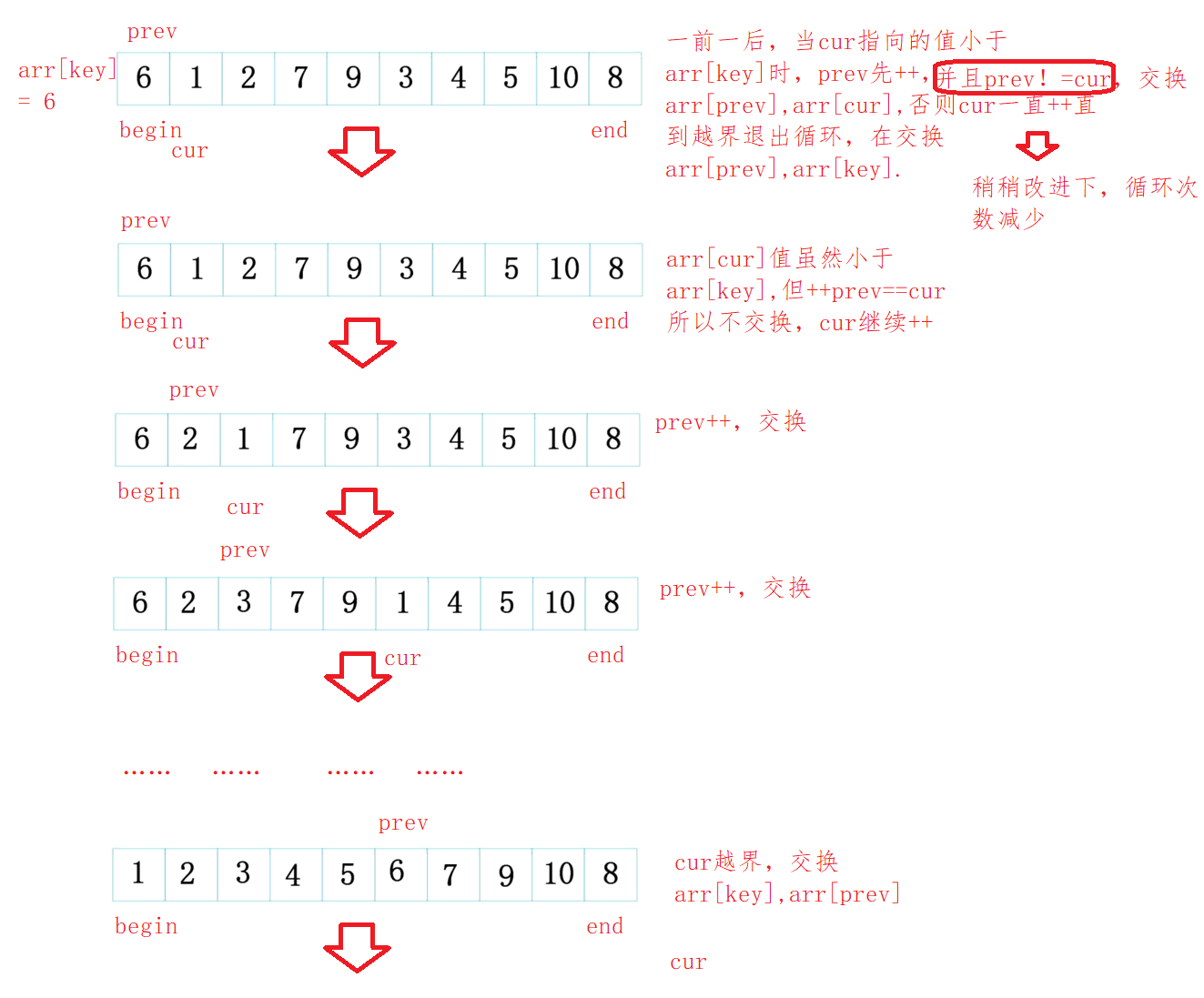
code implementation
public static void partSort2(int []arr,int left,int right){
if(left >= right){
return;
}
int Index = midIndex(arr,left,right);
Swap(arr,left,Index);
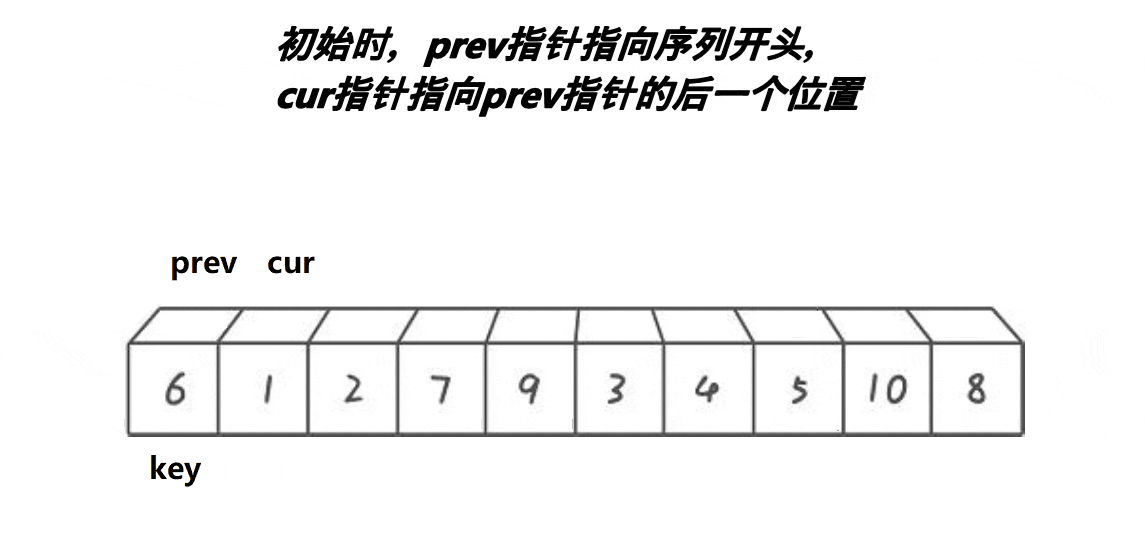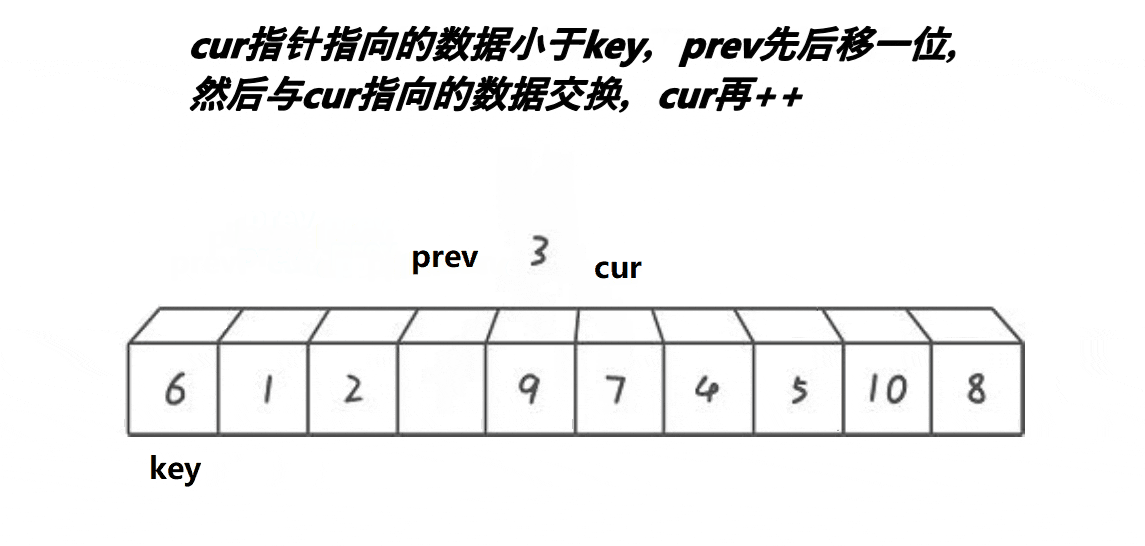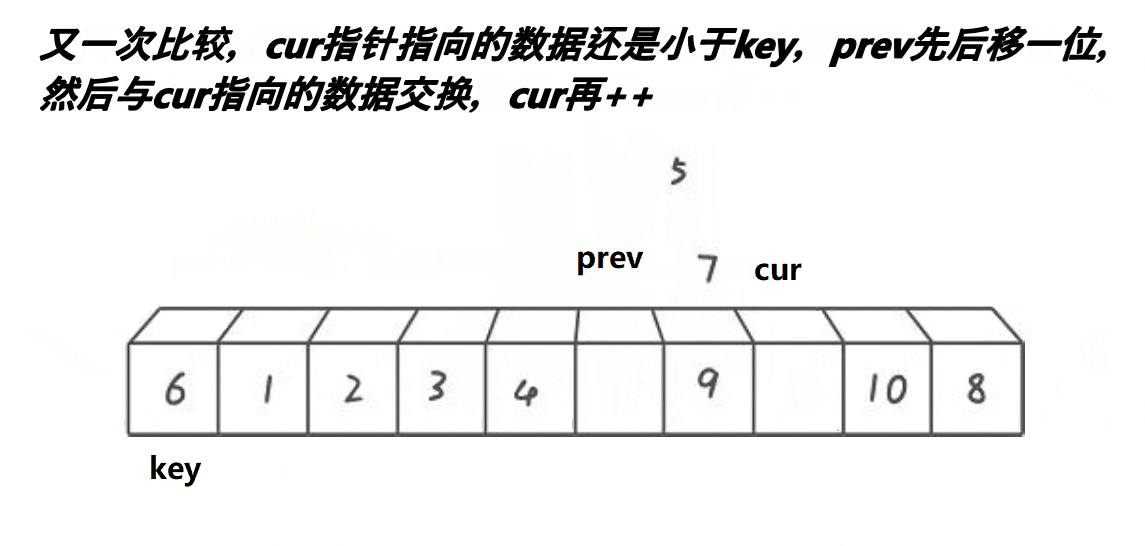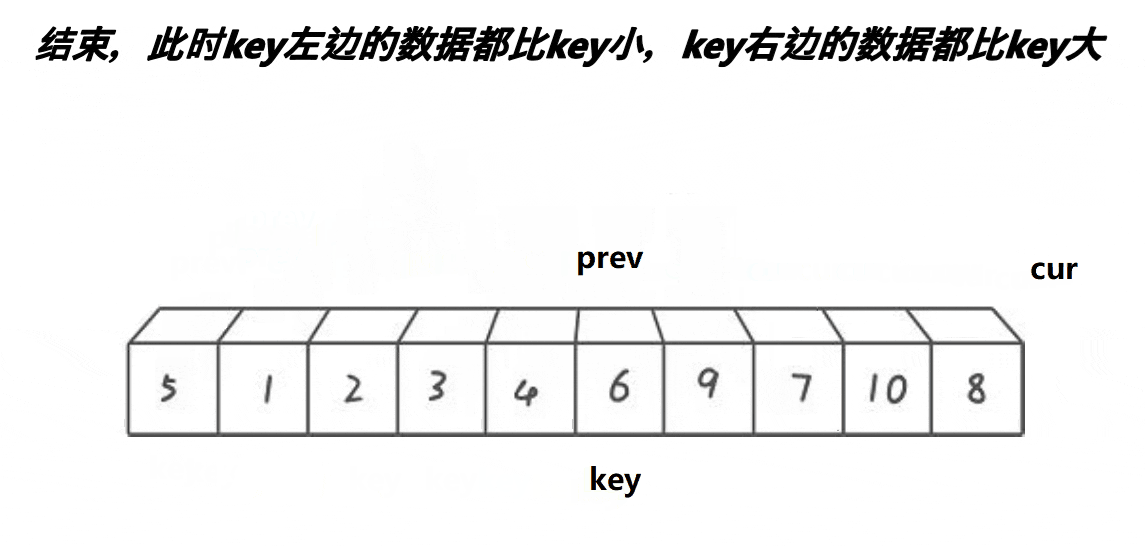
int prev = left;
int cur = left + 1;
int key = left;
while(cur <= right){
while(arr[cur] < arr[key] && ++prev != cur){
Swap(arr,prev,cur);
}
cur++;
}
Swap(arr,key,prev);
partSort2(arr,left,prev-1);
partSort2(arr,prev+1,right);
}Non recursive fast scheduling
Recursion has been used in our previous fast scheduling, but it is not very good, because recursion has a fatal defect: too deep stack frame depth and insufficient stack space will lead to stack overflow.
For example: we find the value of 1 + 2 + 3 +... + n, which is simply realized by recursion
public static int f(int n){
return n == 1 ? 1 : f(n-1)+n;
}10000 times is OK

10w times directly overflow the stack.
 Therefore, non recursive algorithms are used in most companies.
Therefore, non recursive algorithms are used in most companies.
How to use non recursion? We use data structure stack to simulate stack recursion. It is realized by using the characteristics of stack first in and last out.
First, simply transform the front and back pointer method into a single pass sorting:
public static int singleSort(int []arr,int left,int right){//Single express
int begin = left;
int end = right;
int key = begin;
while(begin < end){
while(begin < end && arr[end] >= arr[key]){//Find small
end--;
}
while(begin < end && arr[begin] <= arr[key]){//Find big
begin++;
}
Swap(arr,begin,end);
}
Swap(arr,begin,key);//Exchange the value of the begin position with the value of the key
return begin;
}First, build a stack and put the last element of the array and the subscript of the first element on the stack. Then the two elements in the stack are the intervals of the array to be sorted. Because the stack is last in first out, the first out is the subscript of the first element, which is received with left and the other with right. Then we call the single path sort and give left and right to this function. Finally, the single pass sorting returns a subscript key, and the subscript elements have been arranged. The next step is to determine whether the left range of the key exceeds two or more elements. If it exceeds, continue to row.
Because we want to row the left interval first, we first press the subscripts of the first and last elements of the right interval into the stack, and then press the left interval. Finally, array ordering is realized.
Non recursive code implementation
public static void quickSortNoR(int []arr){
Stack<Integer> stack = new Stack();//Create a stack of integers
stack.push(arr.length-1);//Save last element subscript
stack.push(0);//Save first element subscript
while(!stack.empty()){
int left = stack.pop();//Fetch stack top element
int right = stack.pop();//ditto
int key = singleSort(arr,left,right);
if(key + 1 < right){//Push in right interval element subscript
stack.push(right);
stack.push(key+1);
}
if(left < key - 1){//Push in left interval element subscript
stack.push(key - 1);
stack.push(left);
}
}
stack.clear();//Destroy stack
}Single pass sorting can also use the left and right pointer method, digging method and front and rear pointer method. It is OK to simply change the lower type.
Merge sort
Merge sort is an effective sort algorithm based on merge operation. It is a very typical application of Divide and Conquer. The ordered subsequences are combined to obtain a completely ordered sequence; That is, each subsequence is ordered first, and then the subsequence segments are ordered. If two ordered tables are merged into one, it is called two-way merging. Core steps of merging and sorting:
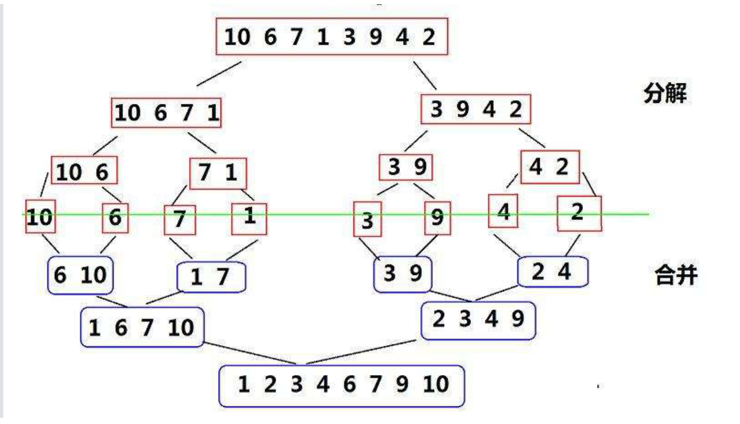
code implementation

class MergeSort{
public static void merge(int []arr,int left,int mid,int right){
int []tmp=new int[arr.length];
int begin1 = left,end1 = mid;
int begin2 = mid+1,end2 = right;
int index = left;
while (begin1 <= mid && begin2 <= end2){
if(arr[begin1] < arr[begin2]){
tmp[index++] = arr[begin1++];
}else {
tmp[index++] = arr[begin2++];
}
}
while(begin1 <= end1){
tmp[index++] = arr[begin1++];
}
while(begin2 <= end2){
tmp[index++] = arr[begin2++];
}
for (int i = left; i <= right; i++) {
arr[i] = tmp[i];
}
}
public static void mergeSort(int []arr,int left,int right){
if(left >= right){
return;
}
int mid = (left+right) / 2;
mergeSort(arr,left,mid);//Divide left interval
mergeSort(arr,mid+1,right);//Partition right interval
merge(arr,left,mid,right);//merge
}
}Time complexity analysis: the merge complexity is O (n), because there are two loops with a combined length of n. Merge has been called logN times in total, which is binary, so the time complexity is O (N *logN);
Space complexity: because it requires merge to construct arrays, the time complexity is O(N);
Stability: stable.
The sharing of this article is over.
Original is not easy, remember three consecutive Oh!!!