Preface

This section will enter the red and black tree section of SGIS TL. As for red-black tree, it is a complex data structure, but it is not particularly difficult. If you don't know much about the red-black tree, you can go online to consult the relevant information, because the main purpose of this paper is to analyze the source code of the red-black tree in STL, which is slightly different from the common red-black tree, but also more complex, and needs a certain basis.

Basic concepts

Firstly, what is a binary search tree? A binary search tree is a binary search tree that conforms to the nature that the value of any node must be greater than that of any node in its left subtree and smaller than that of any node in its right subtree (the value of the node is not allowed to repeat). We call a binary search tree that conforms to this nature. The average efficiency of searching, inserting and deleting binary search tree is O(logn).
But think about a scenario where you insert an incremental array. This makes the binary search tree degenerate into a linked list, and the complexity of the linked list is well known.
In order to solve this problem, a balanced binary search tree is introduced. On the premise that it is still a binary search tree, the balance control is added. Simply put, it is not allowed that the depth difference between the two subtrees of a node is too large. If it exceeds the standard, it will be adjusted.

Briefly introduce the four properties of red-black trees:
1. The root node is black
2. Each node is red or black
3. If a node is red, its left and right child nodes are black.
4. For each node, there are the same number of black nodes in the path from the node to all its descendant leaf nodes.

Red-black tree is a kind of balanced binary search tree. It is not as strict as AVL tree. But because of the above characteristics, a red-black tree with n nodes keeps its height in logn, and its insertion, deletion and search operation time complexity is O(logn), which is a classic and efficient tree in general.

When we insert and delete the red-black tree, it may lead to the red-black tree can not meet the above properties 3 or 4, so we need to operate to adjust the red-black tree, so that it can re-satisfy the nature of a red-black tree. Such operations are left-handed, right-handed, double-handed, etc. Here we do not go to the specific how they rotate, but in the source code analysis.

Source code analysis

With regard to rb_tree, all the source codes are in stl_tree.h. The amount of code needed to implement a complete red-black tree is usually several hundred lines. Because STL needs to be generalized, the amount of code is about 109 lines. About the insertion operation of red-black tree, it is relatively simple, its deletion operation needs a lot of points, and "STL Source Analysis" does not mention the deletion operation, about this, you may need to consult other information and try to follow the drawing to understand.
Next, we analyze it in order of its node settings, iterators, definitions of parts, constructors/destructors, simple member functions, and complex operations.

Node setup

Each node of a red-black tree has one of the red/black colors, represented by true and false in stl.

//Red is false, black is true
typedef bool __rb_tree_color_type;
const __rb_tree_color_type __rb_tree_red = false;
const __rb_tree_color_type __rb_tree_black = true;

//Nodes of red-black trees (Valueless parts)
struct __rb_tree_node_base
{
  typedef __rb_tree_color_type color_type;
  typedef __rb_tree_node_base* base_ptr;

  //The color of the node
  color_type color;
  //Parent node
  base_ptr parent;
  //left child
  base_ptr left;
  //Right child
  base_ptr right;

  /* Finding the Minimum
   * This is an easy task for a binary search tree.
   * Just go left all the way.
   */
  static base_ptr minimum(base_ptr x)
  {
    while (x->left != 0) x = x->left;
    return x;
  }

  /* Searching for Maximum Similarities */
  static base_ptr maximum(base_ptr x)
  {
    while (x->right != 0) x = x->right;
    return x;
  }
};

//Nodes of the red-black tree (complete part)
template <class Value>
struct __rb_tree_node : public __rb_tree_node_base
{
  typedef __rb_tree_node<Value>* link_type;
  Value value_field;
};

Iterator of Red-Black Tree

For the iterator part of the red-black tree, increment and decrement, there are two more bizarre scenarios. This is because SGISTL uses a little trick to implement the red-black tree, and there is a header node on the root node.
When the red-black tree is in its initial state, only the header node (red) has its left and right children pointing to itself. When inserting a node, the parent node of the header points to the root node, the left child point to the smallest node, and the right child point to the largest node.
The diagrams are as follows: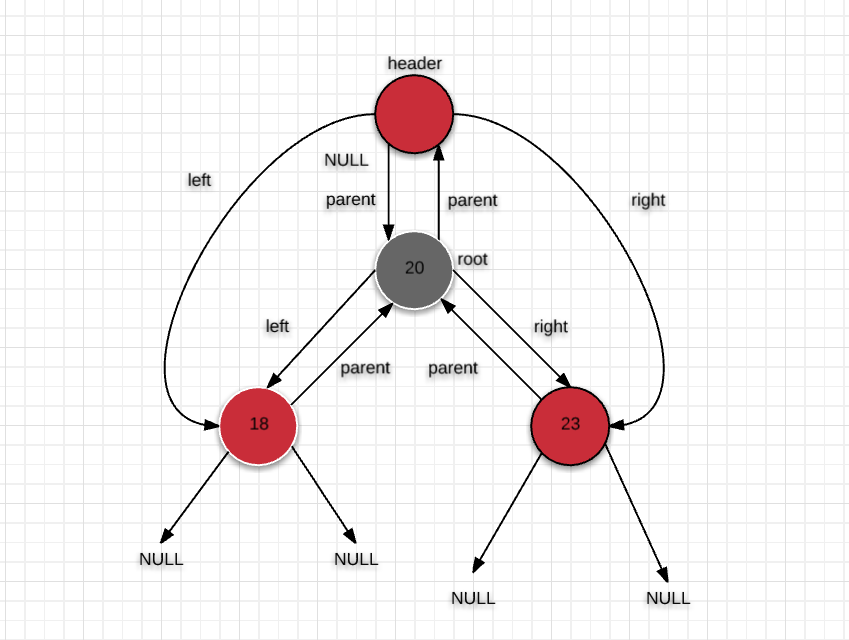

//Basic Classes of Iterators
struct __rb_tree_base_iterator
{
  typedef __rb_tree_node_base::base_ptr base_ptr;
  typedef bidirectional_iterator_tag iterator_category;
  typedef ptrdiff_t difference_type;
  base_ptr node;

  /* Used to implement iterator +
   * In fact, it is to find the next nearest value of the current node's value.
   */
  void increment()
  {
    /* When there is a right subtree, go straight to the left subtree of the right subtree to the bottom.
     * You can find the next value of the current node
     */
    if (node->right != 0) {
      node = node->right;
      while (node->left != 0)
        node = node->left;
    }
    else {
      /* When there is no right subtree, you have to look up.
       * This is because of the characteristics of the binary search tree.
       * Bigger than node values can only be found in the upper layer.
       * If the current node is the right child of its parent node
       * It moves up all the time (because if it is a right child, it is larger than the value of the parent node, so it is not desirable).
       * This value can only be obtained if the current node is the left child of the parent node.
       /

      /* Note here a special case when the node is root and there is no right subtree
       * At this point y is header, and Y - > right = root
       * So it goes through a loop, updating node to header and y to root.
       * At this point, the loop exits because y - > right = null! = node
       * Next, we won't go to node - > right!= y, so let's set node to y.
       * The result is that node points to header
       * This situation is very special. Most of the parts on the Internet are directly copied books. Here, please cooperate with the pictures I drew to understand.
       */
      base_ptr y = node->parent;
      while (node == y->right) {
        node = y;
        y = y->parent;
      }
      /* At this point, the right child of the node is not the parent node.
       * This judgment seems strange, because y is not the parent of node?
       * In fact, to deal with the special case when node is root and root has no right subtree
       * If this is not the case, then node should take the value of its parent node, because node is the left child of y and the value of y is larger than its left subtree.
       */
      if (node->right != y)
        node = y;
    }
  }
  /Heavy load--Operator call
  void decrement()
  {
    /* Here is another special case. It's easy to understand with the above figure.
     * Special case: When node points to header
     * header The color of the header is red, and the parent node of the header's parent node is itself, satisfying the conditions
     * Corresponding to the case where there is only root node in front and there is no right subtree at the root node, the ++ header is used.
     * Here we point to the header and proceed - - it should be the right subtree of the header and the maximum node of the whole red-black tree.
     */
    if (node->color == __rb_tree_red &&
        node->parent->parent == node)
      node = node->right;
    else if (node->left != 0) {
      /* In general, find the nearest node with a smaller value from the current node */
      base_ptr y = node->left;
      while (y->right != 0)
        y = y->right;
      node = y;
    }
    else {
      /* If there is no left subtree, only look up, if the current node is the left child of its parent node.
       * It moves up all the time (because if it's a left child, it's less than the value of the parent node, so it's not advisable)
       * This value can only be obtained if the current node is the right child of the parent node.
       */
      base_ptr y = node->parent;
      while (node == y->left) {
        node = y;
        y = y->parent;
      }
      node = y;
    }
  }
};

//iterator
template <class Value, class Ref, class Ptr>
struct __rb_tree_iterator : public __rb_tree_base_iterator
{
  //Some definitions
  typedef Value value_type;
  typedef Ref reference;
  typedef Ptr pointer;
  typedef __rb_tree_iterator<Value, Value&, Value*>             iterator;
  typedef __rb_tree_iterator<Value, const Value&, const Value*> const_iterator;
  typedef __rb_tree_iterator<Value, Ref, Ptr>                   self;
  typedef __rb_tree_node<Value>* link_type;

  //Constructor
  __rb_tree_iterator() {}
  __rb_tree_iterator(link_type x) { node = x; }
  __rb_tree_iterator(const iterator& it) { node = it.node; }

  //Overload * and - > operators, relatively simple
  reference operator*() const { return link_type(node)->value_field; }
#ifndef __SGI_STL_NO_ARROW_OPERATOR
  pointer operator->() const { return &(operator*()); }
#endif /* __SGI_STL_NO_ARROW_OPERATOR */

  //The overloaded + + operator calls the increment function of the base class.
  self& operator++() { increment(); return *this; }
  self operator++(int) {
    self tmp = *this;
    increment();
    return tmp;
  }

  //Overload -- Operator, which calls the decrement function of the base class
  self& operator--() { decrement(); return *this; }
  self operator--(int) {
    self tmp = *this;
    decrement();
    return tmp;
  }
};

This is the iterator part of the red-black tree, which has such a connection with the nodes of the red-black tree. (The STL Source Anatomy is directly used here.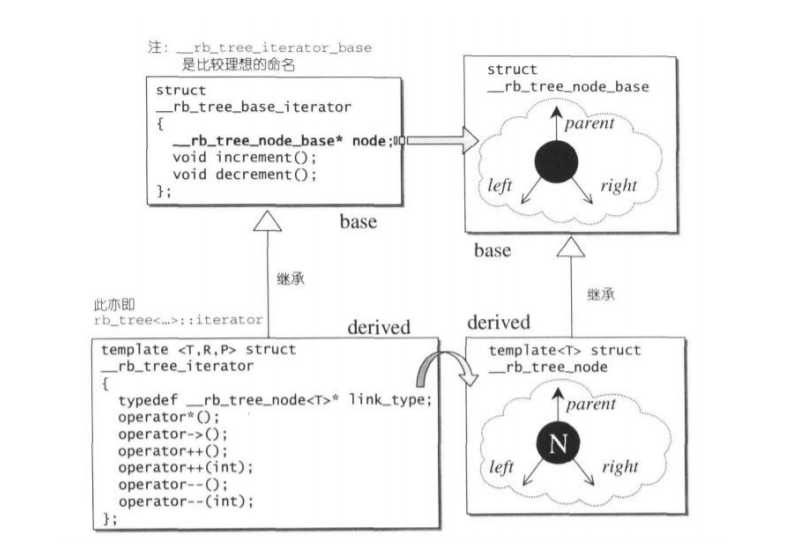

Defining Parts and Constructing/Destructing, Some Simple Membership Functions

This part mainly introduces the definition, initialization and construction of red-black tree, and some simple functions. Complicated operations, such as insertion and deletion, are analyzed in the next section.
Following are the definitions and some functions to get node members.

template <class Key, class Value, class KeyOfValue, class Compare,
          class Alloc = alloc>
/* First of all, we should pay attention to the parameters of the template.
 * key Values on which to store nodes on a red-black tree
 * value That is, the value of the node
 * KeyOfValue It's an imitation function, which is used to get the key through value. As for what the imitation function is, there's no need to know now. We'll do a special analysis later.
 * Compare Standard for comparing key sizes
 * Alloc It's our familiar spatial configurator.
 */
class rb_tree {
protected:
  //Some simple type declarations and proprietary space configurers
  typedef void* void_pointer;
  typedef __rb_tree_node_base* base_ptr;
  typedef __rb_tree_node<Value> rb_tree_node;
  typedef simple_alloc<rb_tree_node, Alloc> rb_tree_node_allocator;
  typedef __rb_tree_color_type color_type;
public:
  typedef Key key_type;
  typedef Value value_type;
  typedef value_type* pointer;
  typedef const value_type* const_pointer;
  typedef value_type& reference;
  typedef const value_type& const_reference;
  typedef rb_tree_node* link_type;
  typedef size_t size_type;
  typedef ptrdiff_t difference_type;
protected:
  //Get a new node (note that it is not initialized)
  link_type get_node() { return rb_tree_node_allocator::allocate(); }
  //Release the specified node
  void put_node(link_type p) { rb_tree_node_allocator::deallocate(p); }
  //Create a node and initialize it to x
  link_type create_node(const value_type& x) {
    link_type tmp = get_node();
    __STL_TRY {
      construct(&tmp->value_field, x);
    }
    __STL_UNWIND(put_node(tmp));
    return tmp;
  }
  //Duplicate nodes, including colors
  link_type clone_node(link_type x) {
    link_type tmp = create_node(x->value_field);
    tmp->color = x->color;
    tmp->left = 0;
    tmp->right = 0;
    return tmp;
  }
  //Destroy node
  void destroy_node(link_type p) {
    destroy(&p->value_field);
    put_node(p);
  }

protected:
  size_type node_count; // keeps track of size of tree
  //header node
  link_type header;
  //Size comparison criteria, because the type of node is not only int and so on, but also may be an object, so we need a size comparison criterion.  
  Compare key_compare;

  /* Get the root node */
  link_type& root() const { return (link_type&) header->parent; }
  /* Get the node with the smallest key value of the red-black tree
   * header The left child points to the node with the smallest key value
   */
  link_type& leftmost() const { return (link_type&) header->left; }
  /* Get the node with the largest key value of the red-black tree
   * header The right child points to the node with the largest key value
   */
  link_type& rightmost() const { return (link_type&) header->right; }

  //Return the left child of the current node
  static link_type& left(link_type x) { return (link_type&)(x->left); }
  static link_type& right(link_type x) { return (link_type&)(x->right); }
  //Return the right child of the current node
  static link_type& parent(link_type x) { return (link_type&)(x->parent); }
  //Get the value of the current node
  static reference value(link_type x) { return x->value_field; }
  //Get the key of the current node through value
  static const Key& key(link_type x) { return KeyOfValue()(value(x)); }
  //Get the color of the current node
  static color_type& color(link_type x) { return (color_type&)(x->color); }

  static link_type& left(base_ptr x) { return (link_type&)(x->left); }
  static link_type& right(base_ptr x) { return (link_type&)(x->right); }
  static link_type& parent(base_ptr x) { return (link_type&)(x->parent); }
  static reference value(base_ptr x) { return ((link_type)x)->value_field; }
  static const Key& key(base_ptr x) { return KeyOfValue()(value(link_type(x)));}
  static color_type& color(base_ptr x) { return (color_type&)(link_type(x)->color); }
  //Get the minimum and maximum
  static link_type minimum(link_type x) {
    return (link_type)  __rb_tree_node_base::minimum(x);
  }
  static link_type maximum(link_type x) {
    return (link_type) __rb_tree_node_base::maximum(x);
  }

public:
  //Declare iterators
  typedef __rb_tree_iterator<value_type, reference, pointer> iterator;
  typedef __rb_tree_iterator<value_type, const_reference, const_pointer>
          const_iterator;

......
private:
  //Define insert, copy, delete operations. Note that the underline is added to prove that they are invoked by insert, copy, delete operations provided to the outside world.
  iterator __insert(base_ptr x, base_ptr y, const value_type& v);
  link_type __copy(link_type x, link_type p);
  void __erase(link_type x);
  //Initialization, the initial state of a red-black tree
  void init() {
    //Apply for header space and set the color red
    header = get_node();
    color(header) = __rb_tree_red; // used to distinguish header from
                                   // root, in iterator.operator++
    /* The root node is empty and the left and right children of the header point to themselves.
     * This usage may be strange to see for the first time, but it's legal because it's a left-valued reference.
     */
    root() = 0;
    leftmost() = header;
    rightmost() = header;
  }

Here's the constructor/destructor section

public:
                                // allocation/deallocation
  //Set size comparison criteria and call init() for initialization
  rb_tree(const Compare& comp = Compare())
    : node_count(0), key_compare(comp) { init(); }
  //copy constructor
  rb_tree(const rb_tree<Key, Value, KeyOfValue, Compare, Alloc>& x)
    : node_count(0), key_compare(x.key_compare)
  {
    //Set header
    header = get_node();
    color(header) = __rb_tree_red;
    /* If x has no root node, it's simpler. Set the left and right child nodes of header to themselves.
     * Otherwise, call the _copy function to copy, set the header, and finally update node_count.
     */
    if (x.root() == 0) {
      root() = 0;
      leftmost() = header;
      rightmost() = header;
    }
    else {
      __STL_TRY {
        root() = __copy(x.root(), header);
      }
      __STL_UNWIND(put_node(header));
      leftmost() = minimum(root());
      rightmost() = maximum(root());
    }
    node_count = x.node_count;
  }
  /* Destructor
   * Call clear to delete all nodes except header
   * Finally, delete the header node
   */
  ~rb_tree() {
    clear();
    put_node(header);
  }
  rb_tree<Key, Value, KeyOfValue, Compare, Alloc>&
  operator=(const rb_tree<Key, Value, KeyOfValue, Compare, Alloc>& x);

Here are some simple functions

public:    
                                // accessors:
  Compare key_comp() const { return key_compare; }
  //Initial iterator is the smallest node
  iterator begin() { return leftmost(); }
  const_iterator begin() const { return leftmost(); }
  //The end iterator is header
  iterator end() { return header; }
  const_iterator end() const { return header; }
  ......
  bool empty() const { return node_count == 0; }
  size_type size() const { return node_count; }
  size_type max_size() const { return size_type(-1); }

Summary

In this section, we understand the node, iterator and partial implementation of red-black tree in SGIS TL, which lays the foundation for the implementation of set and map container. In the next section, we will analyze the complex operations of insertion and deletion.