dijkstra

Premise: in a graph, there can be no edges with negative weight.

Give you a starting point. What is the shortest distance from the starting point to all nodes? If a point cannot be reached, the distance to this point is positive infinity (usually in a directed graph).

For example, see the following figure: the set on the right represents the shortest distance from point A to each point in the set.

At the beginning, it is assumed that the distance from point A to all other points is positive infinity, that is, it is assumed that it is unreachable:

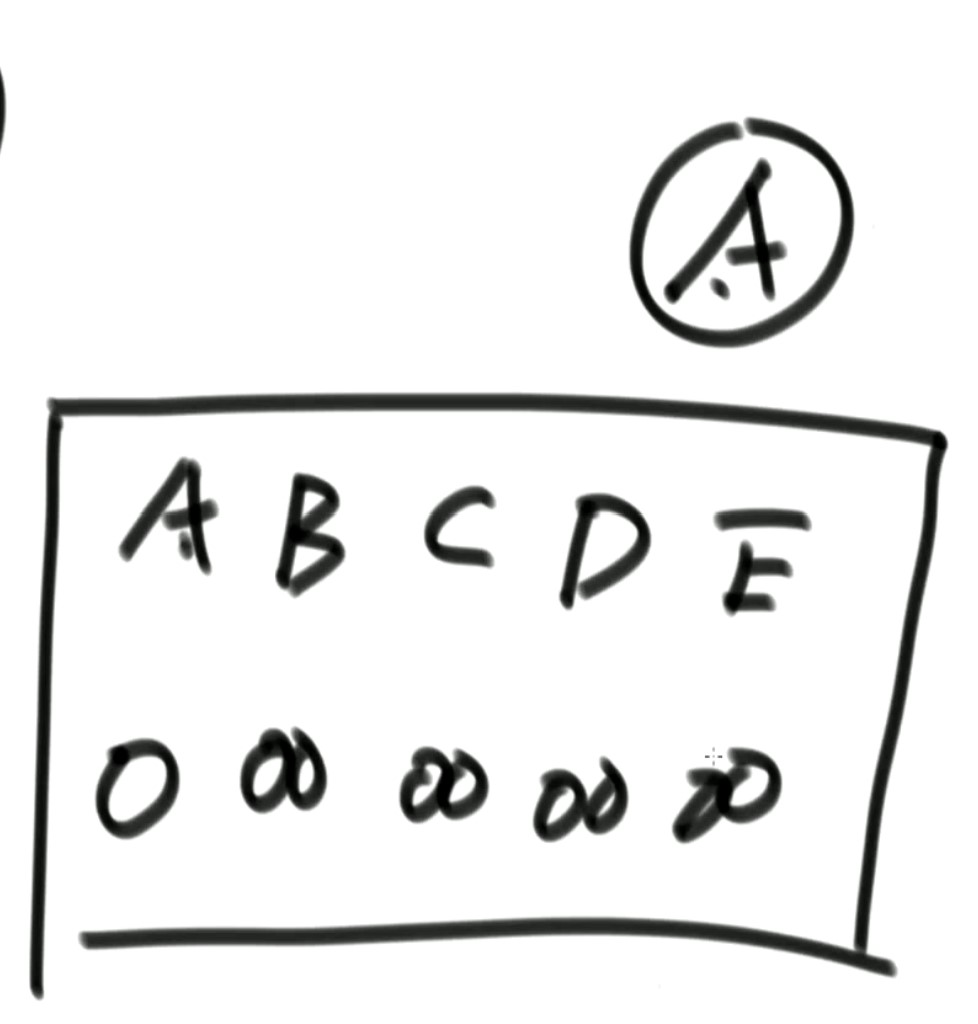
After A appears as A bridge connection point, the distance from A to B is the original distance from A to A (0) plus the distance from A to B (1). The latter is similar, so the following figure is obtained:

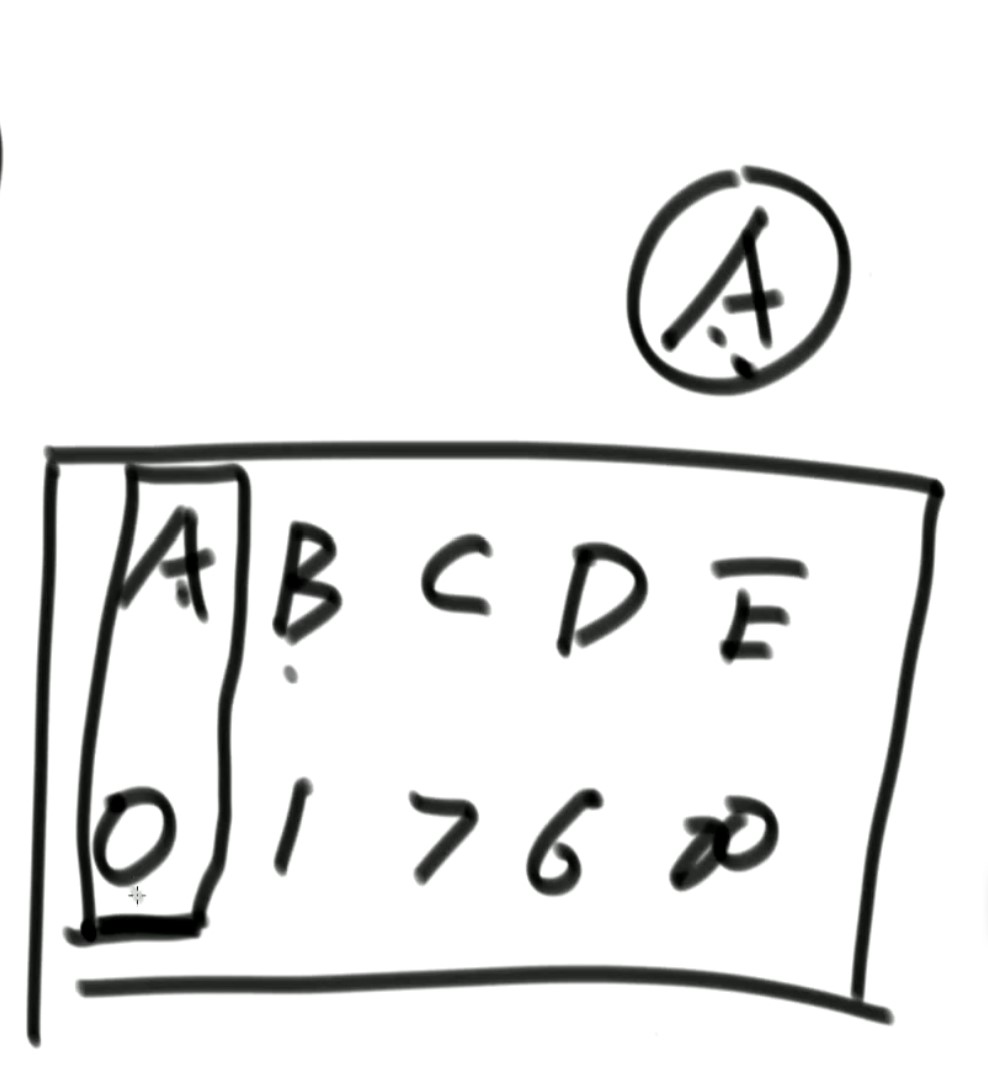
When the record of point A is used up, it will never be changed, that is, point A circled in the figure above. Then select the smallest record among the remaining records; Point B corresponds to 1, which means that the distance from the origin to B is 1, and then take B as the bridge point to look out. It is found that the distance from B to C is 2 and the distance from B to E is 170, so the record of point C in the table can be updated to 3 (AB+BC) and the record of point E to 171 (AB+BE). After that, the record of point B will never be changed. Lock the record used in the table and never touch it again.

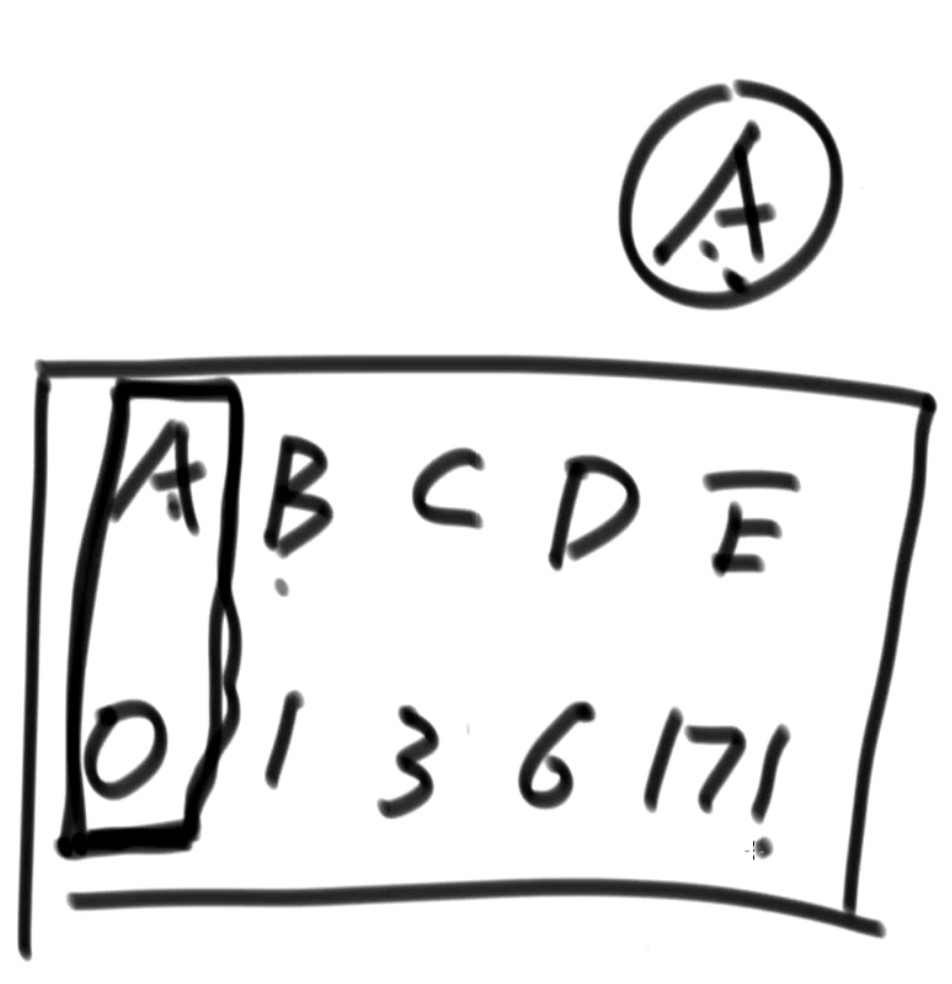
Next, point C... Play with the same logic. Finally, all the locked records in the table are the records required by dijkstra.

Note that if you encounter the same distance in the middle, you can not update it. It seems a little greedy.

But the problem is how to find the smallest record in the table. You can find it every time, but it's a little troublesome. So a better way is to use small root piles.

The small root heap will be automatically organized and the minimum value will be popped out each time. However, we also have a requirement here that we may have to change the values already organized in the heap. In this case, the heap provided by the system cannot be realized. We need to rewrite the heap manually! I recommend reading these two articles—— System provided heap VS manual overwrite heap & Heap sort,, . We can better understand the improvement of dijkstra algorithm.

Then let's take a look at the functions to be realized by our handwritten small root heap,

1) add(), the way to add a record, that is, the distance from the origin to a point, and organize it according to the distance

2) update(), the update method, needs to update the distance of a record. For example, the distance from the origin to point X is 100, but the distance from a bridge point to point X is 20, so the distance of this record should be updated to 20, and this record should be up heapInsert() in the small root heap to automatically organize the order

3) ignore(), a method that ignores a used node.

The structure of the things in the small root pile is:

public static class NodeRecord {
		public Node node;
		public int distance;

		public NodeRecord(Node node, int distance) {
			this.node = node;
			this.distance = distance;
		}
	}

The following code implements two methods of dijkstra algorithm

package com.harrison.class11;

import java.util.HashMap;
import java.util.HashSet;
import java.util.Map.Entry;

import com.harrison.class11.Code01_NodeEdgeGraph.*;

public class Code07_dijkstra {
	// The shortest distance from the from point to the key is value
	public static HashMap<Node, Integer> dijkstra1(Node from) {
		HashMap<Node, Integer> distanceMap = new HashMap<>();
		distanceMap.put(from, 0);// At the beginning, the distance from oneself to oneself is of course 0
		// Lock used records
		HashSet<Node> selectedNodes = new HashSet<>();
		Node minNode=getMinDistanceNodeAndUnselectedNode(distanceMap, selectedNodes);
		while(minNode!=null) {
			int distance=distanceMap.get(minNode);
			for(Edge edge:minNode.edges) {
				Node toNode=edge.to;
				if(!distanceMap.containsKey(toNode)) {
					distanceMap.put(toNode, distance+edge.weight);
				}else {
					distanceMap.put(edge.to, 
							Math.min(distanceMap.get(toNode), distance+edge.weight));
				}
			}
			selectedNodes.add(minNode);
			minNode=getMinDistanceNodeAndUnselectedNode(distanceMap, selectedNodes);
		}
		return distanceMap;
	}

	// Exclude the points in the selectedNodes set in the distanceMap table, and then select the point with the smallest distance to return
	public static Node getMinDistanceNodeAndUnselectedNode(
			HashMap<Node, Integer> distanceMap,
			HashSet<Node> selectedNodes) {
		Node minNode = null;
		int minDistance = Integer.MAX_VALUE;
		// EntrySet can traverse the values in the HashMap
		for(Entry<Node, Integer> entry:distanceMap.entrySet()) {
			Node node=entry.getKey();
			int distance=entry.getValue();
			if(!selectedNodes.contains(node) && distance<minDistance) {
				minNode=node;
				minDistance=distance;
			}
		}
		return minNode;
	}
	
	public static class NodeRecord{
		public Node node;
		public int distance;
		
		public NodeRecord(Node n,int d) {
			node=n;
			distance=d;
		}
	}
	
	public static class NodeHeap{
		// Actual heap structure
		private Node[] nodes;
		// The position of key in the heap is value
		// If value is - 1, it means that this node has been in the heap (it pops up after coming in)
		private HashMap<Node, Integer> heapIndexMap;
		// The minimum distance from the source node to the key is value
		private HashMap<Node, Integer> distanceMap;
		private int size;// How many points are there on the pile
		
		public NodeHeap(int size) {
			nodes=new Node[size];
			heapIndexMap=new HashMap<>();
			distanceMap=new HashMap<>();
			this.size=0;
		}
		
		public boolean isEmpty() {
			return size==0;
		}
		
		// If a node has a record in the heapIndexMap table, it indicates that it has entered the heap
		public Boolean isEntered(Node node) {
			return heapIndexMap.containsKey(node);
		}
		
		public boolean inHeap(Node node) {
			return isEntered(node) && heapIndexMap.get(node)!=-1;
		}
		
		public void heapInsert(Node node,int index) {
			while(distanceMap.get(nodes[index])<distanceMap.get(nodes[(index-1)/2])) {
				swap(index, (index-1)/2);
				index=(index-1)/2;
			}
		}
		
		public void heapfiy(int index,int size) {
			int left=2*index+1;
			while(left<size) {
				int smallest=(left+1<size) &&
							 (distanceMap.get(nodes[left+1])
							 <distanceMap.get(nodes[left]))
							 ?left+1:left;
				smallest=distanceMap.get(nodes[smallest])
						 <distanceMap.get(nodes[index])
						 ?smallest:index;
				if(smallest==index) {
					break;
				}
				swap(smallest, index);
				index=smallest;
				left=2*index+1;
			}
		}
		
		private void swap (int index1,int index2) {
			heapIndexMap.put(nodes[index1], index2);
			heapIndexMap.put(nodes[index2], index1);
			Node tmp=nodes[index1];
			nodes[index1]=nodes[index2];
			nodes[index2]=tmp;
		}
		
		// There is a node. If a node is found, the distance from the source node to the node is distance
		// Judge whether to update or not. If you need to update, update it
		public void addOrUpdateOrIgnore(Node node,int distance) {
			if(inHeap(node)) {
				// If the node is on the heap, the distance may become smaller after updating the records, so the heap needs to be adjusted
				distanceMap.put(node, Math.min(distanceMap.get(node), distance));
				heapInsert(node, heapIndexMap.get(node));
			}
			if(!isEntered(node)){
				// If you have not entered the heap, hang this node at the last node of the heap
				nodes[size]=node;
				// The location of this node is in the size of the heapIndexMap table
				heapIndexMap.put(node, size);
				distanceMap.put(node, distance);
				heapInsert(node, size++);
			}
			// If both if's fail, it means that this node is not on the heap, but it has come in again,
			// It's equivalent to returning directly without doing anything
		}
		
		public NodeRecord pop(){
			NodeRecord nodeRecord=new NodeRecord(nodes[0], distanceMap.get(nodes[0]));
			swap(0, size-1);
			// After the stack top is ejected, mark it as - 1 and remove the corresponding distance record
			heapIndexMap.put(nodes[size-1], -1);
			distanceMap.remove(nodes[size-1]);
			// Release things in size-1 position
			nodes[size-1]=null;
			heapfiy(0, --size);
			return nodeRecord;
		}
	}
	
	// Improved dijkstra algorithm
	// Starting from the head, all nodes that the head can reach
	// Generate the minimum path record to each node and return it
	public static HashMap<Node, Integer> dijkstra2(Node head,int size){
		NodeHeap nodeHeap=new NodeHeap(size);
		nodeHeap.addOrUpdateOrIgnore(head, 0);
		HashMap<Node, Integer> ans=new HashMap<>();
		while(!nodeHeap.isEmpty()) {
			NodeRecord recored=nodeHeap.pop();
			Node cur=recored.node;
			int distance=recored.distance;
			for(Edge edge:cur.edges) {
				nodeHeap.addOrUpdateOrIgnore(edge.to, edge.weight+distance);
			}
			ans.put(cur, distance);
		}
		return ans;
	}
}