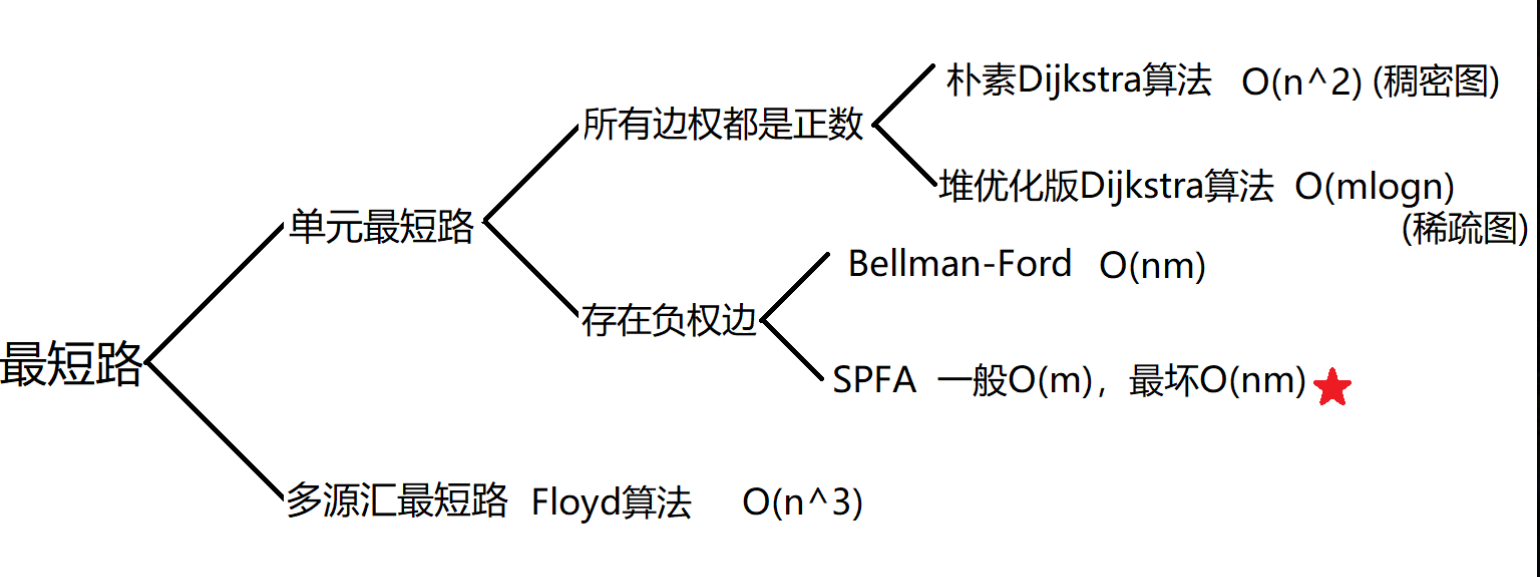
Summary of shortest path algorithm templates
In graph theory, the graph is directed and undirected, and only the algorithm of the directed graph is considered here. For undirected graphs, we see them as a special kind of directed graph, for all undirected edges u ↔ v u \leftrightarrow v u ↔ v is considered yes u → v u\to v u_v and v → u v \to u v→u.
Appointment: n n n represents the number of points in the graph. m m m represents the number of edges in the graph.
Density Map: m m m and n 2 n^2 n2 orders of magnitude are roughly the same
Sparse graph: m m m and n n n orders of magnitude are roughly the same
Mapping
There are two general ways of drawing:
- Adjacency Matrix: Define a two-dimensional array g [ N ] [ N ] g[N][N] g[N][N], g [ i ] [ j ] g[i][j] g[i][j] represents a point i i i and j j Edge weight between j.
- Adjacency table: An array of analogue adjacency tables with a single-chain table for each node that stores all the adjacent edges of the point.
Special, for Bellman_ For the Ford algorithm, we usually define an array of structs to store information for all edges.
Shortest path algorithm
Shortest path algorithms are generally divided into two categories:
-
Single-source shortest path, common algorithms are:
( 1 ) (1) (1)Dijkstra: only if all edges have positive edge weights can be used, algorithm time complexity in dense graph by O ( n 2 ) For O(n^2) Is O(n2), and the algorithm time complexity in the sparse graph is m l o n g ( n ) mlong(n) mlong(n).
( 2 ) (2) (2)Bellman_ford: use when there are negative weighted edges, shortest path problem with limit on number of edges, shortest path problem when there are negative weighted circuits, time complexity is O ( n m ) O(nm) O(nm).
( 3 ) (3) (3)spfa - Bellman_for queue optimization Ford algorithm: time complexity is O ( m ) O(m) O(m), the worst time complexity is O ( n m ) O(nm) O(nm).
-
Multi-source shortest path:
( 1 ) (1) (1) Floyd: Standard Freud algorithm, triple loop. After the cycle ends d [ i ] [ j ] d[i][j] d[i][j] stores points i i i-to-point j j The shortest distance of j. It is important to note that the order of loops does not change: the first layer enumerates the middle points, and the second and third layers enumerate the starting and ending points. Time Complexity O ( n 3 ) O(n^3) O(n3).
Dijkstra algorithm template (including heap optimization)
#include <iostream>
#include <cstring>
#include <algorithm>
using namespace std;
const int N = 510, INF = 0x3f3f3f3f;
int n, m;
int g[N][N];
int dist[N];
bool st[N]; // Determine the set of shortest paths
void dijkstra()
{
memset(dist, 0x3f, sizeof dist);
dist[1] = 0;
for(int i = 0; i < n; i ++)
{
int t = -1;
for(int j = 1; j <= n; j ++) // Find the minimum distance to update other points
if(!st[j] && (t == -1 || dist[t] > dist[j]))
t = j;
// Update Other Points
for(int j = 1; j <= n; j ++)
dist[j] = min(dist[j], dist[t] + g[t][j]);
// Mark the point that has the shortest path determined
st[t] = true;
}
}
int main()
{
cin >> n >> m;
for(int i = 1; i <= n; i ++)
for(int j = 1; j <= n; j ++)
if(i == j) g[i][j] = 0;
else g[i][j] = INF;
while (m -- )
{
int a, b, c;
scanf("%d%d%d", &a, &b, &c);
g[a][b] = min(g[a][b], c);
}
dijkstra();
if(dist[n] == INF) puts("-1");
else printf("%d\n", dist[n]);
return 0;
}
Heap optimized version dijkstra
#include <iostream>
#include <cstring>
#include <algorithm>
#include <queue>
using namespace std;
const int N = 150010, INF = 0x3f3f3f3f;
typedef pair<int, int> PII;
int n, m;
int h[N], e[N], ne[N], w[N], idx;
int dist[N];
bool st[N]; // Set of points to determine the shortest path
void add(int a, int b, int c)
{
e[idx] = b, ne[idx] = h[a], w[idx] = c, h[a] = idx ++;
}
void dijkstra()
{
memset(dist, 0x3f, sizeof dist);
dist[1] = 0;
priority_queue<PII, vector<PII>, greater<PII>> heap;
heap.push({0, 1});
while(heap.size())
{
auto t = heap.top();
heap.pop();
int ver = t.second;
if(st[ver]) continue;
st[ver] = true;
for(int i = h[ver]; i != -1; i = ne[i])
{
int j = e[i];
if(dist[j] > dist[ver] + w[i])// Replace adjacent edges when their distance is greater than the distance updated with the current point
{
dist[j] = dist[ver] + w[i];// d[ver] is the current minimum point distance; w[i] is the weight of the current adjacent edge
heap.push({dist[j], j});
}
}
}
}
int main()
{
cin >> n >> m;
memset(h, -1, sizeof h);
while(m --)
{
int a, b, c;
scanf("%d%d%d", &a, &b, &c);
add(a, b, c);
}
dijkstra();
if(dist[n] == INF) puts("-1");
else printf("%d\n", dist[n]);
return 0;
}
Bellman_Ford algorithm template
Bellman_must be selected to solve the shortest path problem with a limited number of edges Ford
#include <iostream>
#include <cstring>
#include <algorithm>
using namespace std;
const int N = 510, M = 10010, INF = 0x3f3f3f3f;
struct Edge
{
int a, b, w;
}edges[M];
int n, m, k;
int dist[N], backup[N];
void Bellman_Ford()
{
memset(dist, 0x3f, sizeof dist);
dist[1] = 0;
for(int i = 0; i < k; i ++)
{
memcpy(backup, dist, sizeof dist);
for(int j = 0; j < m; j ++)
{
int a = edges[j].a, b = edges[j].b, w = edges[j].w;
dist[b] = min(dist[b], backup[a] + w);
}
}
}
int main()
{
cin >> n >> m >> k;
for(int i = 0; i < m; i ++)
{
int a, b, w;
scanf("%d%d%d", &a, &b, &w);
edges[i] = {a, b, w};
}
Bellman_Ford();
if(dist[n] > INF / 2) puts("impossible");
else printf("%d\n", dist[n]);
return 0;
}
spfa (Queue Optimized Bellman_Ford) algorithm template
spfa algorithm for shortest path
The spfa algorithm is similar to the heap-optimized Dijkstra algorithm in that it is very fast in general
#include <iostream>
#include <cstring>
#include <algorithm>
#include <queue>
using namespace std;
const int N = 100010, INF = 0x3f3f3f3f;
int n, m;
int h[N], e[N], ne[N], w[N], idx;
int dist[N];
bool st[N];
void add(int a, int b, int c)
{
e[idx] = b, ne[idx] = h[a], w[idx] = c, h[a] = idx ++;
}
void spfa()
{
memset(dist, 0x3f, sizeof dist);
dist[1] = 0;
queue<int> q;
q.push(1);
st[1] = true;
while(q.size())
{
int t = q.front();
q.pop();
st[t] = false;
for(int i = h[t]; i != -1; i = ne[i])
{
int j = e[i];
if(dist[j] > dist[t] + w[i])
{
dist[j] = dist[t] + w[i];
if(!st[j])
{
st[j] = true;
q.push(j);
}
}
}
}
}
int main()
{
cin >> n >> m;
memset(h, -1, sizeof h);
while (m -- )
{
int a, b, w;
scanf("%d%d%d", &a, &b, &w);
add(a, b, w);
}
spfa();
if(dist[n] > INF / 2) puts("impossible");
else printf("%d\n", dist[n]);
return 0;
}
Floyd algorithm template
Floyd algorithm template questions
#include <iostream>
#include <cstring>
#include <algorithm>
using namespace std;
const int N = 210, INF = 0x3f3f3f3f;
int g[N][N];
int n, m, Q;
void floyd()
{
for(int k = 1; k <= n; k ++)
for(int i = 1; i <= n; i ++)
for(int j = 1; j <= n; j ++)
g[i][j] = min(g[i][j], g[i][k] + g[k][j]);
}
int main()
{
scanf("%d%d%d", &n, &m, &Q);
for(int i = 1; i <= n; i ++)
for(int j = 1; j <= n; j ++)
if(i == j) g[i][j] = 0;
else g[i][j] = INF;
while(m --)
{
int a, b, c;
scanf("%d%d%d", &a, &b, &c);
g[a][b] = min(g[a][b], c);
}
floyd();
while(Q --)
{
int x, y;
scanf("%d%d", &x, &y);
if(g[x][y] > INF / 2) puts("impossible");
else printf("%d\n", g[x][y]);
}
return 0;
}