Question meaning: here are some points for you. If and only if the shortest path between them and the last edge of node 111 cannot be reached, find the shortest distance from each point to 111.

Because it is the shortest distance from one point to all other points, we consider the shortest path tree with node 111 as the root. For a shortest path tree from 111 to iii after removing the last edge of the shortest path, it must be the following situation: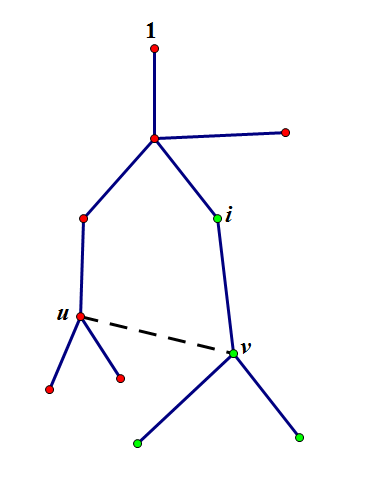

Then we need to find a point pair (u,v), (u,v), (u,v), and there is an edge between u,vu,vu,v, u,v is not in the shortest path tree, vvv is in the subtree of node iii, uuu is not in the subtree of node iii;

2;

Add [v] + w [u,v] to the new graph, and then sort the whole graph from small to large. Then enumerate every point to update ansansans, and use the union query set to maintain whether u, VU, VU and V are connected.

#include<iostream>
#include<cstdio>
#include<algorithm>
#include<queue>
using namespace std;
int head[1001000],dis[1001000],num,n,cnt;
int headd[1001000],fa[1001000],m,ans[1001000];
bool book[1001000];
struct nodee
{
    int next,dis,to,from;
}a[1001000];
inline void add1(int from,int to,int dis)
{
    a[++cnt].next=headd[from];
    a[cnt].from=from;
    a[cnt].to=to;
    a[cnt].dis=dis;
    headd[from]=cnt;
}
priority_queue <pair<int,int> > q;
inline void dij(int start)
{
    for(int i=1;i<=n;i++)
        dis[i]=2147483647;
    dis[start]=0;
    q.push(make_pair(0,start));
    while(!q.empty())
    {
        int x=q.top().second;
        q.pop();
        if(book[x])
        	continue;
        book[x]=1;
        for(int i=headd[x];i!=0;i=a[i].next)
        {
        	int v=a[i].to;
            if(dis[v]>dis[x]+a[i].dis)
            {
                dis[v]=dis[x]+a[i].dis;
                fa[v]=x;
                q.push(make_pair(-dis[v],v));
            }        	
        }

    }
}
struct node
{
    int next,dis,to,from;
}e[1001000];
inline void add(int from,int to,int dis)
{
    e[++num].next=head[from];
    e[num].from=from;
    e[num].to=to;
    e[num].dis=dis;
    head[from]=num;
}
bool cmp(node n1,node n2)
{
	return n1.dis<n2.dis;
}
int f[1001000];
int find(int x)
{
	if(x==f[x])
		return x;
	else
	{
		f[x]=find(f[x]);
		return f[x];
	}
}
void solve(node x)
{
    int u=x.from,v=x.to,d=x.dis;
    while(find(u)!=find(v))
	{ 
        if(dis[find(u)]<dis[find(v)])//deep like operation 
			swap(u,v);
        ans[find(u)]=d-dis[find(u)];
        u=f[find(u)]=fa[find(u)];
    }
}
int main()
{
    scanf("%d%d",&n,&m);
    for(int i=1;i<=m;i++)
    {
    	int u,v,d;
        scanf("%d%d%d",&u,&v,&d);
        add1(u,v,d);
        add1(v,u,d);
    }
    dij(1);
    for(int i=1;i<=cnt;i++)
    {
    	int u=a[i].from,v=a[i].to;
    	if(u!=fa[v]&&v!=fa[u])//Edge not on shortest path tree
    		add(u,v,dis[u]+dis[v]+a[i].dis);
	}
	sort(e+1,e+num+1,cmp);
	for(int i=1;i<=n;i++)
	{
		f[i]=i;
		ans[i]=1<<30;
	}
	for(int i=1;i<=num;++i)
		solve(e[i]);
    for(int i=2;i<=n;i++)
   	{
   		if(ans[i]==1<<30)
   			printf("-1\n");
   		else
   			printf("%d\n",ans[i]);
	}
    return 0;
}