Greed and proof

To choose the greedy strategy, we must first prove that the greedy strategy is correct before we can consider using it. In many cases, the rationality of greed is not obvious, but if we can find a counterexample, it can prove that such greed is not correct.

Fractional Knapsack Problem

Fractional Knapsack Problem
When the items with knapsack problem can be cut arbitrarily, the greedy strategy is correct. That's easy to understand. Just take the commodity with the highest unit value and fill the bag is the optimal solution.
ac Code:

#include <iostream>
#include <algorithm>
using namespace std;

int n, t;
const int N = 110;

struct Coin
{
	double v;
	double w;
	double val;
	bool operator<(const Coin& c) const
	{
		return val < c.val;
	}
}coin[N];

int main()
{
	cin >> n >> t;
	for(int i = 0; i < n; i++)
	{
		double w, v;
		cin >> w >> v;
		coin[i] = {v, w, v / w};
	} 
	sort(coin, coin + n);
	double ans = 0;
	for(int i = n - 1; i >= 0; i--)
	{
		if(t < coin[i].w)
		{
			ans += coin[i].val * t;
			t = 0;	
			break;
		} 
		else if(t > 0)
		{
			t -= coin[i].w;
			ans += coin[i].v;
		}
	}
	printf("%.2lf", ans);
}

But how to prove that the greedy strategy is wrong when the backpack problem item cannot be cut?
Counter evidence can be used. As long as there is an example that can prove that greed is wrong, it cannot be used. (this example is easy to find. The test case given is one)

Line up to receive water

There are n people queuing in front of a faucet to receive water. If the time for each person to receive water is Ti, please program to find out a sequence of n people queuing, so as to minimize the average waiting time of n people.

The problem is intuitively simple. The minimum average waiting time is to allow fewer people to wait for water for a long time, that is, the shorter the time, the more people will receive water first.

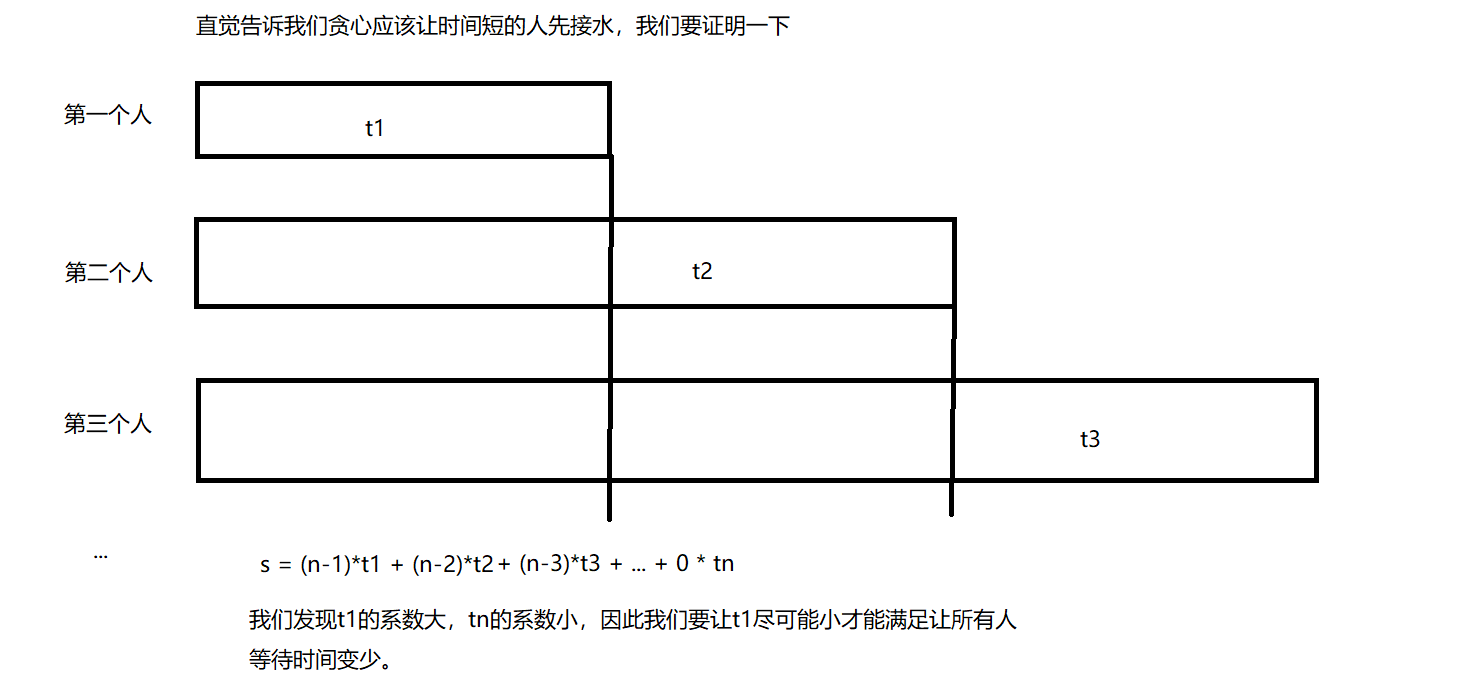
In fact, it's OK not to prove it. You can give some examples. If you can't give a counterexample, it proves that greed is correct. Violent enumeration can be used to verify the answer. If the answers of violence and greed are consistent, greed is highly correct.

ac code

#include <iostream>
#include <algorithm>
using namespace std;

const int N = 1010;

struct P
{
	int id, t;
	bool operator< (const P& p) const
	{
		if(t == p.t) return id < p.id;
		else return t < p.t;
	}
}p[N];

int main()
{
	int n;
	cin >> n;
	for(int i = 1; i <= n; i++)
	{
		int t;
		cin >> t;
		p[i] = {i , t};
	}
	sort(p + 1, p + n + 1);
	double res = 0;
	int u = n;
	for(int i = 1; i <= n; i++)
	{
		res += p[i].t * (u - 1);
		u --;
		cout << p[i].id << ' ';
	}
	puts("");
	printf("%.2lf", res / n);
}

Messy yyy / segment coverage

Segment coverage
This is a classic greedy problem. Given n intervals, at most several intervals are non coincident and non intersecting.

Idea: look from left to right and find the one with the most left ending position. This can give more space for the later section. In this step, it is the local optimal solution. Then continue to find the leftmost interval and put it if you can (it is possible that the interval is more left, but there is overlap, so you can't put it).

In this way, each step is the local optimal solution, that is, the global optimal solution.

So we just sort by end position in ascending order.

ac code

#include <iostream>
#include <algorithm>

using namespace std;

const int N = 1e6 + 10;

struct Contest
{
	int begin, end;
	bool operator< (const Contest& c) const
	{
		return end < c.end;
	}
}contest[N];

int main()
{
	int n;
	cin >> n;
	for(int i = 0; i < n; i++)
	{
		int b, e;
		cin >> b >> e;
		contest[i] = {b , e};	
	}
	sort(contest, contest + n);
	
	int ans = 0, end = -1;
	for(int i = 0; i < n; i++)
		if(contest[i].begin >= end) 
		{
			ans++;
			end = contest[i].end;
		}
	cout << ans;
}