jdk1.7 -: it is composed of array + linked list. The array is the main body. The linked list mainly exists to solve hash conflicts (i.e. the array index values calculated through the key are the same) (the "zipper method" solves conflicts). jdk1.8 +: it is composed of array + linked list + red black tree. There are great changes in resolving hash conflicts. When the length of the linked list is greater than the threshold (the boundary value of the red black tree is 8 by default) and the current array length is greater than 64, the data storage structure at this index position will be transformed into a red black tree. Add: before the linked list is converted into a red black tree, even if the threshold is greater than 8, but the array length is less than 64, the linked list will not be changed into a red black tree, but the capacity of the array will be expanded. The purpose is: when the array is small, try to avoid the red black tree structure. In the case of red trees, the efficiency of these operations will be reduced because the red trees will become black. At the same time, when the array length is less than 64, the search time is relatively faster. Therefore, as mentioned above, in order to improve performance, the linked list is converted into a red black tree only when the underlying threshold is greater than 8 and the array length is greater than 64. For details, please refer to the treeifyBin() method. Of course, although the red black tree is added as the underlying data structure, the structure becomes complex, but when the threshold is greater than 8 and the array length is greater than 64, the efficiency becomes more efficient when the linked list is converted to red black tree.
1. The access of HashMap is out of order
2. NULL is allowed in all cases
3. In the case of multithreading, this class is safe, and HashTable can be considered.
4. The bottom layer of JDk8 is array + linked list + red black tree, and the bottom layer of JDK7 is array + linked list.
5. Initial capacity and load factor are the key points that determine the performance of the whole class. Don't move easily.
6. HashMap is created lazily. It will be built only when you put data
7. When converting a one-way linked list into a red black tree, it will first change into a two-way linked list and finally into a red black tree. The two-way linked list and the red black tree coexist. Remember.
8. For the two key s passed in, it will be forced to judge the height. The main purpose of judging the height is to decide whether to turn left or right.
9. After the linked list is transferred to the red black tree, efforts will be made to integrate the root node of the red black tree, the head node of the linked list and the table[i] node into one.
10. When deleting, first judge whether the number of red and black trees of deleted nodes needs to be transferred to the linked list. If not, it is similar to RBT. Find an appropriate node to fill in the deleted nodes.
11. The root node of the red black tree is not necessarily the same as the table[i], that is, the head node of the linked list. The synchronization of the three is realized by MoveRootToFront. And hashiterator Remove() will call removeNode with movable=false.
Static variable
/** Serialization version number */
private static final long serialVersionUID = 362498820763181265L;
/** The set initialization capacity must be the n-th power of 2. The default initial capacity is 16 */
static final int DEFAULT_INITIAL_CAPACITY = 1 << 4;
/** The maximum capacity of the set, which is the 30th power of 2 by default */
static final int MAXIMUM_CAPACITY = 1 << 30;
/** Default load factor, default 0.75 */
static final float DEFAULT_LOAD_FACTOR = 0.75f;
/** When the number of elements in the linked list exceeds this value, it will turn into a red black tree (new in jdk1.8) */
static final int TREEIFY_THRESHOLD = 8;
/** When the value of the linked list is less than 6, it will be transferred back from the red black tree to the linked list */
static final int UNTREEIFY_THRESHOLD = 6;
/** When the number of stored elements exceeds this value, the bucket in the table can be converted into a red black tree. Otherwise, when the elements in the bucket exceed the specified conditions, it will only be expanded */
static final int MIN_TREEIFY_CAPACITY = 64;
/** Array structure */
transient Node<K,V>[] table;
/**Store cached data */
transient Set<Map.Entry<K,V>> entrySet;
/**Number of stored elements */
transient int size;
/** It is used to record the modification times of HashMap, that is, the counter for each expansion and change of map structure */
transient int modCount;
/** Capacity expansion critical value: when the number of stored elements exceeds the critical value (capacity * load factor), capacity expansion will be carried out */
int threshold;
/** Hash table load factor */
final float loadFactor;Data structure for storing elements
static class Node<K,V> implements Map.Entry<K,V> {
final int hash;
final K key;
V value;
Node<K,V> next;
Node(int hash, K key, V value, Node<K,V> next) {
this.hash = hash;
this.key = key;
this.value = value;
this.next = next;
}
public final K getKey() { return key; }
public final V getValue() { return value; }
public final String toString() { return key + "=" + value; }
public final int hashCode() {
return Objects.hashCode(key) ^ Objects.hashCode(value);
}
public final V setValue(V newValue) {
V oldValue = value;
value = newValue;
return oldValue;
}
public final boolean equals(Object o) {
if (o == this)
return true;
if (o instanceof Map.Entry) {
Map.Entry<?,?> e = (Map.Entry<?,?>)o;
if (Objects.equals(key, e.getKey()) &&
Objects.equals(value, e.getValue()))
return true;
}
return false;
}
}Constructor
1. Custom capacity and load factors
2. Custom capacity, default load factor 0.75
3. Default capacity 16, default load factor 0.75
4. Pass in a map
/**
* Constructor specifying capacity size and load factor
* @param initialCapacity capacity
* @param loadFactor Load factor
*/
public HashMap(int initialCapacity, float loadFactor) {
// Judge whether the initialization capacity initialCapacity is less than 0. If it is less than 0, an illegal parameter exception IllegalArgumentException will be thrown
if (initialCapacity < 0)
throw new IllegalArgumentException("Illegal initial capacity: " +
initialCapacity);
// Judge whether the initialization capacity is greater than the maximum capacity of the set_ Capability, if yes, the maximum value is used
if (initialCapacity > MAXIMUM_CAPACITY)
initialCapacity = MAXIMUM_CAPACITY;
// Judge whether the load factor loadFactor is less than or equal to 0 or whether it is a non numeric value
if (loadFactor <= 0 || Float.isNaN(loadFactor))
throw new IllegalArgumentException("Illegal load factor: " +
loadFactor);
// Assign the specified load factor to the load factor loadFactor of the HashMap member variable
this.loadFactor = loadFactor;
this.threshold = tableSizeFor(initialCapacity);
}
/**
* Formulate the constructor of capacity size. The default load factor of 0.75 is used
* @param initialCapacity Capacity
*/
public HashMap(int initialCapacity) {
this(initialCapacity, DEFAULT_LOAD_FACTOR);
}
/**
* Constructor using default capacity 16 and default load factor 0.75
*/
public HashMap() {
this.loadFactor = DEFAULT_LOAD_FACTOR; // all other fields defaulted
}
/**
Construct a new HashMap whose mapping is the same as the specified map.
*/
public HashMap(Map<? extends K, ? extends V> m) {
this.loadFactor = DEFAULT_LOAD_FACTOR;
putMapEntries(m, false);
}The above 1, 2 and 3 construction methods will call the following methods
/**
* Returns the n-th power of the smallest 2 larger than the specified initialization capacity,
* For example, if the specified capacity is 11, return 16
*/
static final int tableSizeFor(int cap) {
int n = cap - 1;
n |= n >>> 1;
n |= n >>> 2;
n |= n >>> 4;
n |= n >>> 8;
n |= n >>> 16;
return (n < 0) ? 1 : (n >= MAXIMUM_CAPACITY) ? MAXIMUM_CAPACITY : n + 1;
}If the customized capacity is greater than the 30th power of 2, the capacity defaults to the 30th power of 2; If the customized capacity is not the n-th power of 2, the capacity is changed to the n-th power of the closest customized 2 that is greater than the customized capacity, for example,
/** The actual capacity is 16 */ Map<String, String> map = new HashMap<>(11);
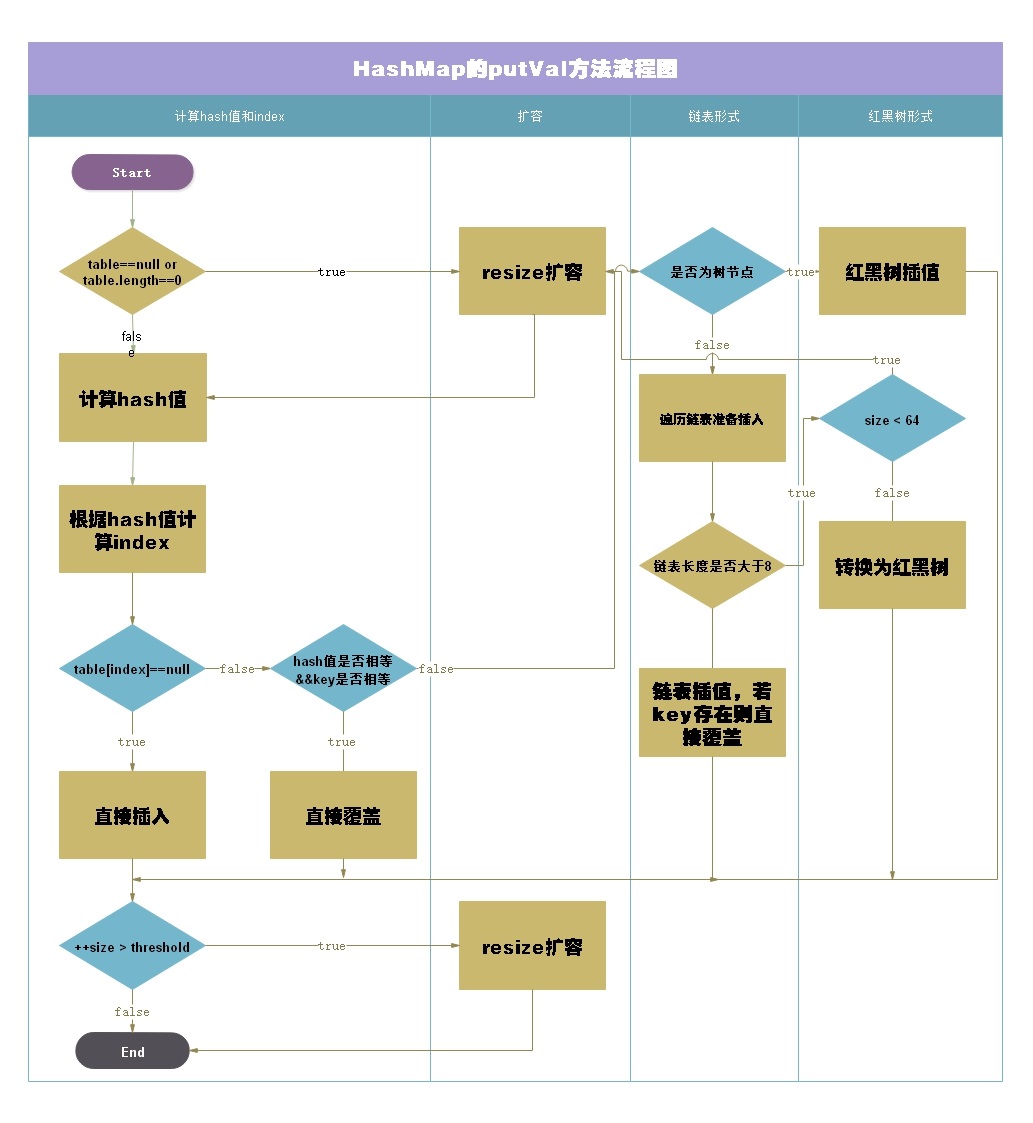
put operation
Steps:
1. First, hash the key to get the subscript of the bucket to be stored
2. Judge whether there is value on the bucket. If not, store it directly; If yes, a hash conflict was encountered:
a. judge whether the key to be inserted is consistent with the conflicting key value. If so, update the value;
b. judge whether the conflicting node of the bucket is a TreeNode (red black tree structure). If so, call the insertion method putTreeNode() of the red black tree
c. the last case is that the conflict node uses the linked list structure to cycle through the linked list. If there is the same key, update the value. If not, insert the node at the end; Judge whether the length of the linked list is greater than or equal to 8. If so, call the method treeifyBin converted into red black tree. In this method, the length of the array will be checked. If it is less than MIN_TREEIFY_CAPACITY=64 will expand the capacity of the array, so it does not necessarily turn into a red black tree.
3. If the size is greater than the threshold (capacity * load factor), expand the capacity;
final V putVal(int hash, K key, V value, boolean onlyIfAbsent,
boolean evict) {
Node<K,V>[] tab; Node<K,V> p; int n, i;
// Judge whether the collection is newly created, that is, the tab is null
if ((tab = table) == null || (n = tab.length) == 0)
n = (tab = resize()).length;
// Calculate whether an element already exists at the node location. If it exists, it indicates that there is a collision conflict. If not, insert the element directly into the location
// Save the existing bucket data to the variable p
if ((p = tab[i = (n - 1) & hash]) == null)
// Create a new node and store it in the bucket
tab[i] = newNode(hash, key, value, null);
// Execute else to explain that tab[i] is not equal to null, indicating that this location already has a value
else {
Node<K,V> e; K k;
// 1. The element hash values are equal, but it cannot be determined that they are the same value
// 2. Whether the key is the same instance or whether the values are equal
if (p.hash == hash &&
((k = p.key) == key || (key != null && key.equals(k))))
// Note: the hash values of the two elements are equal, and the value of the key is also equal. Assign the whole object of the old element to e and record it with E
e = p;
// If the hash values are not equal or the key s are not equal; Judge whether p is a red black tree node
else if (p instanceof TreeNode)
// Put it in the tree
e = ((TreeNode<K,V>)p).putTreeVal(this, tab, hash, key, value);
// Description is a linked list node
// 1) If it is a linked list, you need to traverse to the last node and insert it
// 2) Loop traversal is used to judge whether there are duplicate key s in the linked list
else {
for (int binCount = 0; ; ++binCount) {
// Determine whether p.next reaches the tail of the linked list
// Take out p.next and assign it to e
if ((e = p.next) == null) {
// Insert the node into the tail of the linked list
p.next = newNode(hash, key, value, null);
// Judge whether the critical condition for converting to red black tree is met. If so, call treeifyBin to convert to red black tree
// Note: the treeifyBin method will check the array length if it is less than min_ TREEIFY_ Capability will expand the capacity of the array
if (binCount >= TREEIFY_THRESHOLD - 1)
// Although the judgment here is 7 > = 7, because binCount starts from 0, it has been inserted at the eighth node
// Convert to red black tree
treeifyBin(tab, hash);
// Jump out of loop
break;
}
// If the end of the linked list is not reached, judge whether the key value is the same
if (e.hash == hash &&
((k = e.key) == key || (key != null && key.equals(k))))
// If the key s are equal, the loop jumps out
break;
// It indicates that the newly added element is not equal to the current node. Continue to find the next node.
// Used to traverse the linked list in the bucket. Combined with the previous e = p.next, you can traverse the linked list
p = e;
}
}
// Indicates that a node whose key value and hash value are equal to the inserted element is found in the bucket
// That is to say, a duplicate key is found through the above operation, so here is to change the value of the key into a new value and return the old value
// The modification function of put method is completed here
if (e != null) { // existing mapping for key
// Record the value of e
V oldValue = e.value;
if (!onlyIfAbsent || oldValue == null)
// Update value
e.value = value;
// Post access callback
afterNodeAccess(e);
// Return old value
return oldValue;
}
}
// Record modification times
++modCount;
// Judge whether the actual size is greater than the threshold. If it exceeds the threshold, expand the capacity
if (++size > threshold)
// Capacity expansion
resize();
// Post insert callback
afterNodeInsertion(evict);
return null;
}Operation of hash value
/**
* Returns the hash value of the key
*/
static final int hash(Object key) {
int h;
/*
1)If key equals null: the returned value is 0
2)If the key is not equal to null: first calculate the hashCode of the key, assign it to h, and then move it 16 bits to the right without sign with H
Perform bitwise XOR on binary to get the final hash value
*/
return (key == null) ? 0 : (h = key.hashCode()) ^ (h >>> 16);
}putTreeNode()
Find the root node first, and then judge whether to find the key from the left or the right.
If found, the found node will be returned directly.
If it is not found, create a new node, put the new node in the appropriate position, and consider the node insertion of red black tree and two-way linked list.
/**
* Node insertion of red black tree
*/
final TreeNode<K,V> putTreeVal(HashMap<K,V> map, Node<K,V>[] tab,
int h, K k, V v) {
Class<?> kc = null; // class object defining k
boolean searched = false; // Indicates whether the tree has been traversed once, not necessarily from the root node
TreeNode<K,V> root = (parent != null) ? root() : this; // If the parent node is not empty, find the root node. If it is empty, it is the root node itself
// The traversal starts from the root node and has no termination conditions. You can only exit from the inside
for (TreeNode<K,V> p = root;;) {
// Declare the search direction, the hash value of the current node, and the current node
int dir, ph; K pk;
if ((ph = p.hash) > h) // If the hash value of the current node is greater than the hash value of the specified key
dir = -1; // The node to be inserted should be to the left of the current node
else if (ph < h) // If the hash value of the current node is less than the hash value of the specified key
dir = 1; // The node to be inserted should be to the right of the current node
else if ((pk = p.key) == k || (k != null && k.equals(pk))) // If the hash value and key of the current node are the same as the specified key
return p; // Return to this node
else if ((kc == null &&
(kc = comparableClassFor(k)) == null) ||
(dir = compareComparables(kc, k, pk)) == 0) {
if (!searched) {
TreeNode<K,V> q, ch;
searched = true;
if (((ch = p.left) != null &&
(q = ch.find(h, k, kc)) != null) ||
((ch = p.right) != null &&
(q = ch.find(h, k, kc)) != null))
return q;
}
dir = tieBreakOrder(k, pk);
}
TreeNode<K,V> xp = p;
if ((p = (dir <= 0) ? p.left : p.right) == null) {
Node<K,V> xpn = xp.next;
TreeNode<K,V> x = map.newTreeNode(h, k, v, xpn);
if (dir <= 0)
xp.left = x;
else
xp.right = x;
xp.next = x;
x.parent = x.prev = xp;
if (xpn != null)
((TreeNode<K,V>)xpn).prev = x;
moveRootToFront(tab, balanceInsertion(root, x));
return null;
}
}
}flow chart
get operation
Steps:
1. Calculate the hash value of the key to be queried. If the bucket corresponding to the hash is empty, null is returned;
2. If the bucket is not empty, judge whether the key to be queried is equal to the bucket key. If equal, return the elements in the bucket;
If not, judge whether the bucket has the next node. If not, return null;
3. If there is a next node, judge whether the bucket node is a red black tree node. If so, call the method getTreeNode() of the red black tree to get the node and return the node to be queried; If it is not a red black tree node, it is a linked list node. Traverse the linked list and return the node to be queried.
final Node<K,V> getNode(int hash, Object key) {
Node<K,V>[] tab; Node<K,V> first, e; int n; K k;
// If the hash table is not empty and the bucket corresponding to the key is not empty
if ((tab = table) != null && (n = tab.length) > 0 &&
(first = tab[(n - 1) & hash]) != null) {
// Determine whether the array elements are equal
// Check the position of the first element according to the index
// Note: always check the first element
if (first.hash == hash &&
((k = first.key) == key || (key != null && key.equals(k))))
return first;
// If the array is not the element to be found, judge whether there is the next node at that position
if ((e = first.next) != null) {
// The next node is the red black tree node
if (first instanceof TreeNode)
// Judge whether it is a red black tree. If yes, call the getTreeNode method in the red black tree to obtain the node
return ((TreeNode<K,V>)first).getTreeNode(hash, key);
do {
// Linked list node, loop through the linked list
if (e.hash == hash &&
((k = e.key) == key || (key != null && key.equals(k))))
return e;
} while ((e = e.next) != null);
}
}
return null;
}getTreeNode()
Get the root node, left node and right node first.
Search the data step by step according to the left node < root node < right node.
If the Comparable method is implemented, it is directly compared.
Otherwise, if the root node does not match, the find lookup function will be called recursively
final TreeNode<K,V> getTreeNode(int h, Object k) {
// Call the root() method to get the root node, and then search the red black tree
return ((parent != null) ? root() : this).find(h, k, null);
}
/**
* Get the root node of red black tree
*/
final TreeNode<K,V> root() {
for (TreeNode<K,V> r = this, p;;) {
if ((p = r.parent) == null)
return r;
r = p;
}
}
final TreeNode<K,V> find(int h, Object k, Class<?> kc) {
// Root node
TreeNode<K,V> p = this;
do {
int ph, dir; K pk;
TreeNode<K,V> pl = p.left, pr = p.right, q;
// Check left or right according to the hash value
if ((ph = p.hash) > h)
p = pl;
else if (ph < h) // Check left or right according to the hash value
p = pr;
else if ((pk = p.key) == k || (k != null && k.equals(pk))) // If the key and hash values of this node are the same as those to be checked
return p; // Return to this node
else if (pl == null) // If the left is empty, traverse the right
p = pr;
else if (pr == null) // The right side is empty, and the left side is traversed
p = pl;
else if ((kc != null ||
(kc = comparableClassFor(k)) != null) &&
(dir = compareComparables(kc, k, pk)) != 0)
p = (dir < 0) ? pl : pr;
else if ((q = pr.find(h, k, kc)) != null)
return q;
else
p = pl;
} while (p != null);
return null;
}remove operation
Steps:
1. Calculate the hash value of the key to be deleted, which is similar to the get operation to obtain the node to be deleted
2. After obtaining the node to be deleted, judge the type of the node:
If it is a bucket element, the deletion method is to assign the next node of the bucket to the bucket
If it is a red black tree node, call the red black tree removeTreeNode method to delete the node
If it is a linked list node, delete the node according to the non head node deletion method of the linked list
final Node<K,V> removeNode(int hash, Object key, Object value,
boolean matchValue, boolean movable) {
Node<K,V>[] tab; Node<K,V> p; int n, index;
// Find the location according to the hash
// If the bucket mapped to the current key is not empty
// Assign the element corresponding to the bucket to traversal p
if ((tab = table) != null && (n = tab.length) > 0 &&
(p = tab[index = (n - 1) & hash]) != null) {
Node<K,V> node = null, e; K k; V v;
// If the node on the bucket is the key to be found, point the node to the node
if (p.hash == hash &&
((k = p.key) == key || (key != null && key.equals(k))))
node = p;
// Indicates that the node has a next node
else if ((e = p.next) != null) {
// Note: if the conflict is handled by the red black tree, obtain the node to be deleted by the red black tree
if (p instanceof TreeNode)
node = ((TreeNode<K,V>)p).getTreeNode(hash, key);
else {
// Judge whether to handle hash conflicts in the way of linked list. If yes, traverse the linked list to find the node to be deleted
do {
if (e.hash == hash &&
((k = e.key) == key ||
(key != null && key.equals(k)))) {
node = e;
break;
}
p = e;
} while ((e = e.next) != null);
}
}
// Compare whether the value of the found key matches the one to be deleted
if (node != null && (!matchValue || (v = node.value) == value ||
(value != null && value.equals(v)))) {
// Delete the node by calling the method of red black tree
if (node instanceof TreeNode)
((TreeNode<K,V>)node).removeTreeNode(this, tab, movable);
else if (node == p)
// Array deletion
tab[index] = node.next;
else
// Linked list deletion
p.next = node.next;
// Record modification times
++modCount;
// Number of changes
--size;
// Callback
afterNodeRemoval(node);
return node;
}
}
return null;
}resize() capacity expansion
Each capacity expansion is doubled. Compared with the original (n - 1) - hash result, there is only one bit more, so the node is either in the original position or assigned to the position of "original position + old capacity".
Therefore, during HashMap capacity expansion, you do not need to recalculate the hash. You only need to see whether the new bit of the original hash value is 1 or 0. If it is 0, the index remains unchanged, and if it is 1, the index becomes "original location + old capacity"
Steps:
1. Get the old table data. If the old table is large enough, it will not be expanded, and only the threshold will be adjusted.
2. The expanded range of the old table also meets the requirements, and the container size and threshold are directly expanded.
3. If it is a constructor with parameters, you need to copy the threshold to the container capacity.
4. Otherwise, it is considered that the container has not passed parameters during initialization and needs to be initialized.
5. If the old table has data, the new one changes size and is set, but the threshold is not set successfully. At this point, set a new threshold.
6. Create a new container.
7. The successful expansion of the old table to the new one involves data transfer.
If the data is not empty and is a separate node, the new location will be directly re hash ed.
If the data is not empty, followed by a linked list, you should distinguish the linked list data to see which are assigned to the old place and which are assigned to the new place.
If the node type is a red black tree, call split
/**
* Each capacity expansion is doubled. Compared with the original (n - 1) - hash result, there is only one bit more, so the node is either in the original position or assigned to the position of "original position + old capacity".
* Therefore, during HashMap capacity expansion, you do not need to recalculate the hash. You only need to see whether the new bit of the original hash value is 1 or 0. If it is 0, the index remains unchanged, and if it is 1, the index becomes "original location + old capacity"
* @return the table
*/
final Node<K,V>[] resize() {
// Get the current array
Node<K,V>[] oldTab = table;
// Returns 0 if the current array is equal to null length, otherwise returns the length of the current array
int oldCap = (oldTab == null) ? 0 : oldTab.length;
// The current threshold value is 12 (16 * 0.75) by default
int oldThr = threshold;
int newCap, newThr = 0;
// If the length of the old array is greater than 0, start to calculate the size after capacity expansion
// Less than or equal to 0, there is no need to expand the capacity
if (oldCap > 0) {
// If you exceed the maximum value, you won't expand any more, so you have to collide with you
if (oldCap >= MAXIMUM_CAPACITY) {
// Modify the threshold to the maximum value of int
threshold = Integer.MAX_VALUE;
return oldTab;
}
// The capacity is expanded by 2 times
// The new capacity cannot exceed the size of 2 ^ 30
// The original capacity is greater than or equal to initialization DEFAULT_INITIAL_CAPACITY=16
else if ((newCap = oldCap << 1) < MAXIMUM_CAPACITY &&
oldCap >= DEFAULT_INITIAL_CAPACITY)
// Double the threshold
newThr = oldThr << 1; // double threshold
}
// If the original capacity is less than or equal to 0 and the original threshold point is greater than 0
else if (oldThr > 0) // initial capacity was placed in threshold
// The original threshold is assigned to the new array length
newCap = oldThr;
else { // zero initial threshold signifies using defaults
// If it is not satisfied, the default value is used directly
newCap = DEFAULT_INITIAL_CAPACITY;
newThr = (int)(DEFAULT_LOAD_FACTOR * DEFAULT_INITIAL_CAPACITY);
}
// If the original capacity is less than or equal to 0 and the original threshold point is greater than 0, then newThr is 0
// Calculate the new resize maximum upper limit
if (newThr == 0) {
float ft = (float)newCap * loadFactor;
newThr = (newCap < MAXIMUM_CAPACITY && ft < (float)MAXIMUM_CAPACITY ?
(int)ft : Integer.MAX_VALUE);
}
// The default value of the new threshold is 12 times 2 and then becomes 24
threshold = newThr;
// Create a new hash table
@SuppressWarnings({"rawtypes","unchecked"})
//newCap is the new array length
Node<K,V>[] newTab = (Node<K,V>[])new Node[newCap];
table = newTab;
// The original array is not empty
if (oldTab != null) {
// Move each bucket into a new bucket
// Traverse each bucket of the original hash table and recalculate the new position of the elements in the bucket
for (int j = 0; j < oldCap; ++j) {
Node<K,V> e;
if ((e = oldTab[j]) != null) {
// The original data is assigned null to facilitate GC recycling
oldTab[j] = null;
// Determine whether the array has the next reference
if (e.next == null)
// There is no next reference, indicating that it is not a linked list. There is only one key value pair on the current bucket, which can be inserted directly
newTab[e.hash & (newCap - 1)] = e;
// Judge whether it is a red black tree
else if (e instanceof TreeNode)
// If the description is a red black tree to handle the conflict, call relevant methods to separate the tree
((TreeNode<K,V>)e).split(this, newTab, j, oldCap);
// Using linked list to deal with conflicts
else { // preserve order
Node<K,V> loHead = null, loTail = null;
Node<K,V> hiHead = null, hiTail = null;
Node<K,V> next;
// Calculate the new position of the node through the principle explained above
do {
next = e.next;
// Here we judge that if it is equal to true e, the node does not need to move its position after resizing
if ((e.hash & oldCap) == 0) {
if (loTail == null)
loHead = e;
else
loTail.next = e;
loTail = e;
}
else {
if (hiTail == null)
hiHead = e;
else
hiTail.next = e;
hiTail = e;
}
} while ((e = next) != null);
if (loTail != null) {
loTail.next = null;
newTab[j] = loHead;
}
if (hiTail != null) {
hiTail.next = null;
newTab[j + oldCap] = hiHead;
}
}
}
}
}
return newTab;
}
Turn linked list into red black tree treeifyBin()
Before the linked list is converted into a red black tree, even if the threshold is greater than 8, but the array length is less than 64, the linked list will not be changed into a red black tree, but the capacity of the array will be expanded.
The purpose is: when the array is small, try to avoid the red black tree structure. In the case of red trees, the efficiency of these operations will be reduced because the red trees will become black. At the same time, when the array length is less than 64, the search time is relatively faster. Therefore, as mentioned above, in order to improve performance, the linked list is converted into a red black tree only when the underlying threshold is greater than 8 and the array length is greater than 64
/**
* Convert the linked list into a red black tree
*/
final void treeifyBin(Node<K,V>[] tab, int hash) {
int n, index; Node<K,V> e;
// If the current array is empty or the length of the array is less than the threshold for tree formation (min_tree_capability = 64), expand the capacity.
// Instead of turning the node into a red black tree.
// Objective: if the array is very small, it is less efficient to convert the red black tree and traverse it.
// At this time, if the capacity is expanded, the hash value will be recalculated, the length of the linked list may be shortened, and the data will be put into the array, which is relatively more efficient.
if (tab == null || (n = tab.length) < MIN_TREEIFY_CAPACITY)
// Capacity expansion
resize();
// Get the bucket element of the key hash value and judge whether it is empty
else if ((e = tab[index = (n - 1) & hash]) != null) {
// Perform steps
// 1. First convert the element into a red black tree node
// 2. Then set it as a linked list structure
// 3. Finally, the linked list structure is transformed into a red black tree
// hd: head node of red black tree tl: tail node of red black tree
TreeNode<K,V> hd = null, tl = null;
do {
// Replace the current bucket node with a red black tree node
TreeNode<K,V> p = replacementTreeNode(e, null);
// For the first operation, the red black tree tail node is empty
if (tl == null)
// Assign the p node of the newly created key to the head node of the red black tree
hd = p;
else {
p.prev = tl; // Assign the previous node p to the previous node of the current P
tl.next = p; // Take the current node p as the next node of the tail node of the tree
}
tl = p;
// Until the loop reaches the end of the linked list, and the linked list elements are replaced with red black tree nodes
} while ((e = e.next) != null);
// Let the first element in the bucket, that is, the element in the array, point to the node of the new red black tree,
// In the future, the elements in this bucket are red and black trees instead of linked list data structures
if ((tab[index] = hd) != null)
hd.treeify(tab);
}
}
/**
* Turn the linked list into a red black tree
* @return root of tree
*/
final void treeify(Node<K,V>[] tab) {
TreeNode<K,V> root = null;
// Traverse each TreeNode in the linked list. The current node is x
for (TreeNode<K,V> x = this, next; x != null; x = next) {
next = (TreeNode<K,V>)x.next;
x.left = x.right = null;
//For the first tree node, the root of the current red black tree = = null, so the first node is the root of the tree and is set to black
if (root == null) {
x.parent = null;
x.red = false;
root = x;
}
else {
K k = x.key;
int h = x.hash;
Class<?> kc = null;
//Traverse from the root node to find the insertion position of the current node x
for (TreeNode<K,V> p = root;;) {
int dir, ph;
K pk = p.key;
if ((ph = p.hash) > h) //If the hash value of the current node is less than the hash value of the root node, the direction dir = -1;
dir = -1;
else if (ph < h) //If the hash value of the current node is greater than the hash value of the root node, the direction dir = 1;
dir = 1;
//If the key of node X does not implement the comparable interface, or its key is equal to the key of the root node (k.compareTo(x) == 0), the arbitration insertion rule
//Only when the type K of K directly implements the comparable < k > interface, can it return the class of K. otherwise, null will be returned, and indirect implementation will not work.
else if ((kc == null &&
(kc = comparableClassFor(k)) == null) ||
(dir = compareComparables(kc, k, pk)) == 0)
//Arbitration insertion rules
dir = tieBreakOrder(k, pk);
TreeNode<K,V> xp = p;
if ((p = (dir <= 0) ? p.left : p.right) == null) { //If the left and right nodes of p are not null, continue the for loop, otherwise execute the insertion
x.parent = xp;
if (dir <= 0) //Dir < = 0, insert to left node
xp.left = x;
else //Otherwise, it is inserted into the right node
xp.right = x;
//Adjust the tree after insertion to make it conform to the nature of red black tree
root = balanceInsertion(root, x);
break;
}
}
}
}
// Point the bucket element node to the root node of the red black tree
moveRootToFront(tab, root);
}Red black tree into linked list untreeify
/**
* Turn the red black tree into a linked list, and the number of nodes < = 6 will trigger
* this node.
*/
final Node<K,V> untreeify(HashMap<K,V> map) {
Node<K,V> hd = null, tl = null; // hd points to the head node and tl points to the tail node
for (Node<K,V> q = this; q != null; q = q.next) {// The structure of red black tree and two-way linked list coexist. Here, the chain header node starts to traverse
Node<K,V> p = map.replacementNode(q, null); // Convert each node into a linked list node
if (tl == null)
hd = p;
else
tl.next = p;
tl = p;
}
// Returns the head node of the converted linked list
return hd;
}problem
1. Under what circumstances may the capacity be expanded
When put, putAll, and parameter passing are map s
2. Under what circumstances does the linked list turn into a red black tree
When the number of nodes > = 8 and the array length is greater than 64
3. When will the red and black tree turn into a linked list
When deleting a tree node or expanding capacity, it may
4. Finding the point to be inserted in JDK8 is through = = tail interpolation = = (similar to queuing at the back), while in JDK7 is = = front interpolation = = (similar to plugging at the front. The reason for this is that HashMap inventors believe that the rear insertion section has a higher probability of being accessed)