I don't know how long I haven't written a blog,,, of course I will continue to write after the final exam (although the final exam is very rubbish). I donated 300r to the Blue Bridge Cup some time ago. I don't learn some algorithms in winter vacation. I feel sorry for the money. I'll write a blog to record the learning process and review it. (some final grades came out, which was deeply hit)

Using C + + is more suitable for participating in such competitions, and we don't have to worry about learning a new language, because if we only learn algorithms, we use the STLS of C and C + +, and we only need to accumulate these STLS one by one, that is, we can learn one when we use one, and we can also use our own array implementation, so algorithm learning should not need too much foundation, but, Please be familiar with recursion, recursion and other basic contents, which is very important for understanding the algorithm.
introduce:

Sorting is a commonly used algorithm. In the initial C stage, we will write bubble sorting, but there is no doubt that the time complexity of O(n2) is not acceptable to us. Therefore, we will introduce some better sorting methods. They all have their own application scenarios. Being familiar with their principles is the basis for learning to apply.

Quick sort

As the name suggests, it is a fast sorting method. There are many ways to realize fast sorting. I'll choose a simpler method to explain here.
We adopt an idea similar to divide and conquer, divide an interval into two intervals, find a way to make the numbers in the first interval less than or equal to the numbers in the second interval, and then divide the two intervals into two intervals respectively, and the numbers in the former interval are less than or equal to the numbers in the latter interval. In this way, we keep dividing, and finally the whole array is orderly. The idea is there, but how do we achieve it?
In fact, it's not difficult. We just need to select a defined value first, and then put the numbers greater than or equal to this value in the second interval, and the numbers less than or equal to this value in the first interval to complete the first step. In the follow-up, we can complete the sorting as long as we continuously recursively operate each interval.
If you don't say much, go directly to the code + sample for detailed explanation, which is more conducive to understanding.

/*
Sample
5(Represents the number of numbers to sort)
3 1 2 4 5(Number to sort)
*/
#include<iostream>
using namespace std;
const int N=1e5+10;//Develop the good habit of writing algorithms
int n;
int arr[N];
void myqsort(int l,int r){
    if(l>=r)    return ;//If there is only one number in the current interval, you don't need to continue and return directly
    //Because we write it as + + i, - J below, i should be initialized to l-1 and j to r+1
    int i=l-1,j=r+1,mid=arr[l+r>>1];//mid is the defined value. The > > operator has lower priority and does not need parentheses. It is equivalent to (l+r)/2, but the bit operation is faster
    while(i<j){
    //There is no need to worry about the cross-border problem of i and j, because they will at least encounter the number of this defined value
        while(arr[++i]<mid);//Search for numbers greater than or equal to mid from the left
        while(arr[--j]>mid);//Search for numbers less than or equal to mid from the right
        if(i<j) swap(arr[i],arr[j]);//If I < J, swap two numbers
    }
    //Then sort the two intervals respectively
    myqsort(l,j);
    myqsort(j+1,r);
}
int main(){
    cin>>n;
    for(int i=0;i<n;i++){
        cin>>arr[i];
    }
    myqsort(0,n-1);
    for(int i=0;i<n;i++){
        cout<<arr[i]<<" ";
    }
    return 0;
}

Let's take a look at how our program calculates for this example:
In the figure, i and j represent subscripts, mid represents defined values, and l and r represent the left and right endpoints of the interval

In fact, you can choose any number of mid, but the middle is the best, because there may be special cases. When you choose the leftmost or rightmost number as mid, it may take a lot of time, resulting in timeout. Interested readers can think by themselves.
In fact, when we really write algorithm problems, we generally don't need to write fast scheduling by ourselves. The c + + header file < algorithm > provides us with fast scheduling functions.
The first parameter is the start position to sort, and the second parameter is the last position of the end position. We can also customize a function and use it as the last parameter to define various types of sorting
sort(arr,arr+n,cmp);
In this way, it seems useless to write by yourself?
Not necessarily, when we encounter the following problem:

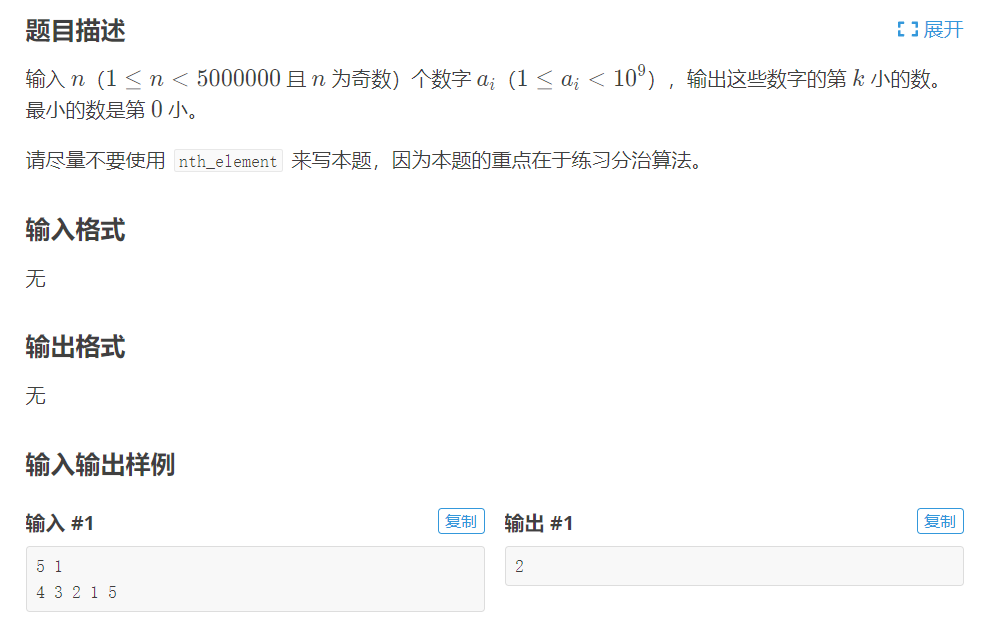
If you use the sort function, you may timeout, but c + + still provides a powerful function -- nth_element(), we want to know about Baidu. Here we use our own handwritten quick row to optimize it
In fact, the idea is very simple. If the smaller number k is on the left, we will only sort on the left, otherwise we will sort on the right, which can save a lot of time.

#include<iostream>
using namespace std;
const int N=1e5+10;
int n,k;
int arr[N];
void myqsort(int l,int r){
    if(l>=r)    return ;
    int i=l-1,j=r+1,mid=arr[l+r>>1];
    while(i<j){
        while(arr[++i]<mid);
        while(arr[--j]>mid);
        if(i<j) swap(arr[i],arr[j]);
    }
    if(k-1<=j)
        myqsort(l,j);
    else
        myqsort(j+1,r);
}
int main(){
    ios::sync_with_stdio(false);
    cin.tie(0);
    cout.tie(0);
    cin>>n>>k;
    for(int i=0;i<n;i++){
        cin>>arr[i];
    }
    myqsort(0,n-1);
    cout<<arr[k-1];
    return 0;
}

Merge sort

Merging and sorting also adopts the idea of division and rule. You may think, I'm almost in line. Why do you still learn this? But when you encounter the following problem:

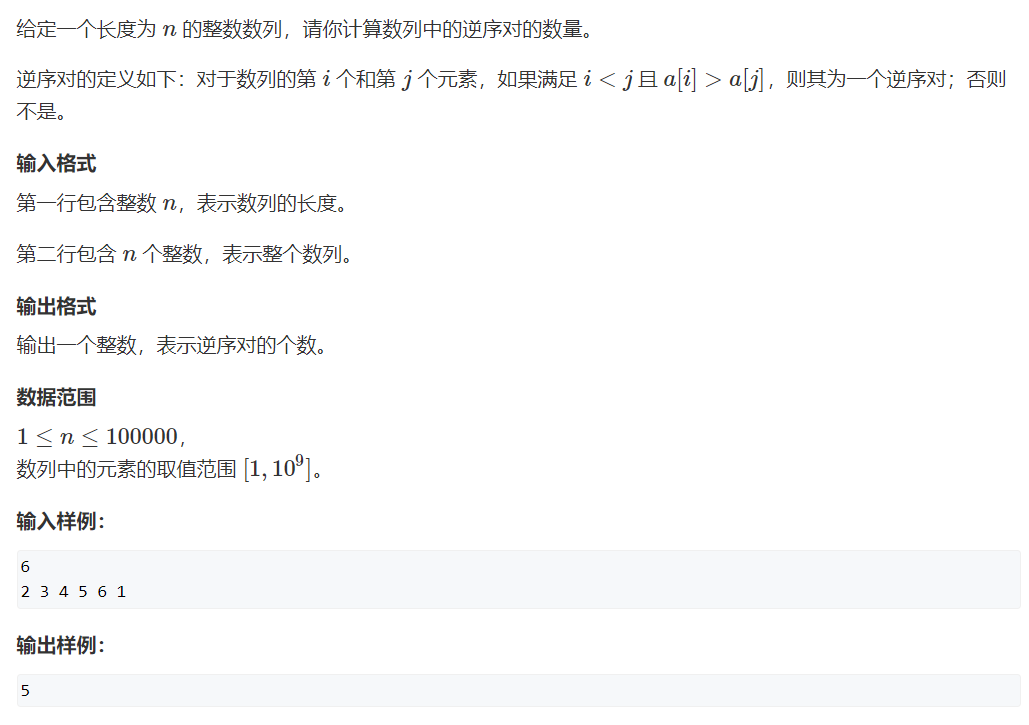
Violent solution is a method, but it will time out. To know an O(nlogn) solution to this problem, we need to understand the merging sort first.

#include<iostream>
using namespace std;
const int N=1e5+10;
int n;
int arr[N],tmp[N];
void merge_sort(int l, int r){
    if(l>=r)    return ;
    int mid=l+r>>1;
    merge_sort(l,mid);
    merge_sort(mid+1,r);
    int i=l,j=mid+1,s=0;
    while(i<=mid&&j<=r){
        if(arr[i]<arr[j])   tmp[s++]=arr[i++];
        else tmp[s++]=arr[j++];
    }
    while(i<=mid) tmp[s++]=arr[i++];
    while(j<=r) tmp[s++]=arr[j++];
    for(int i=l;i<=r;i++){
        arr[i]=tmp[i-l];
    }
}
int main(){
    ios::sync_with_stdio(false);
    cin.tie(0);
    cout.tie(0);
    cin>>n;
    for(int i=0;i<n;i++){
        cin>>arr[i];
    }
    merge_sort(0,n-1);
    for(int i=0;i<n;i++){
        printf("%d ",arr[i]);
    }
    return 0;
}

What effect does the above code have? We use an example to understand it

5
3 1 2 4 5

In fact, we are equivalent to dividing the whole array into two parts, sorting the two parts respectively, and finally sorting the whole array. In this way, the whole array will be orderly. Here we open an additional temporary array for easier operation.
The whole sorting process is as follows:

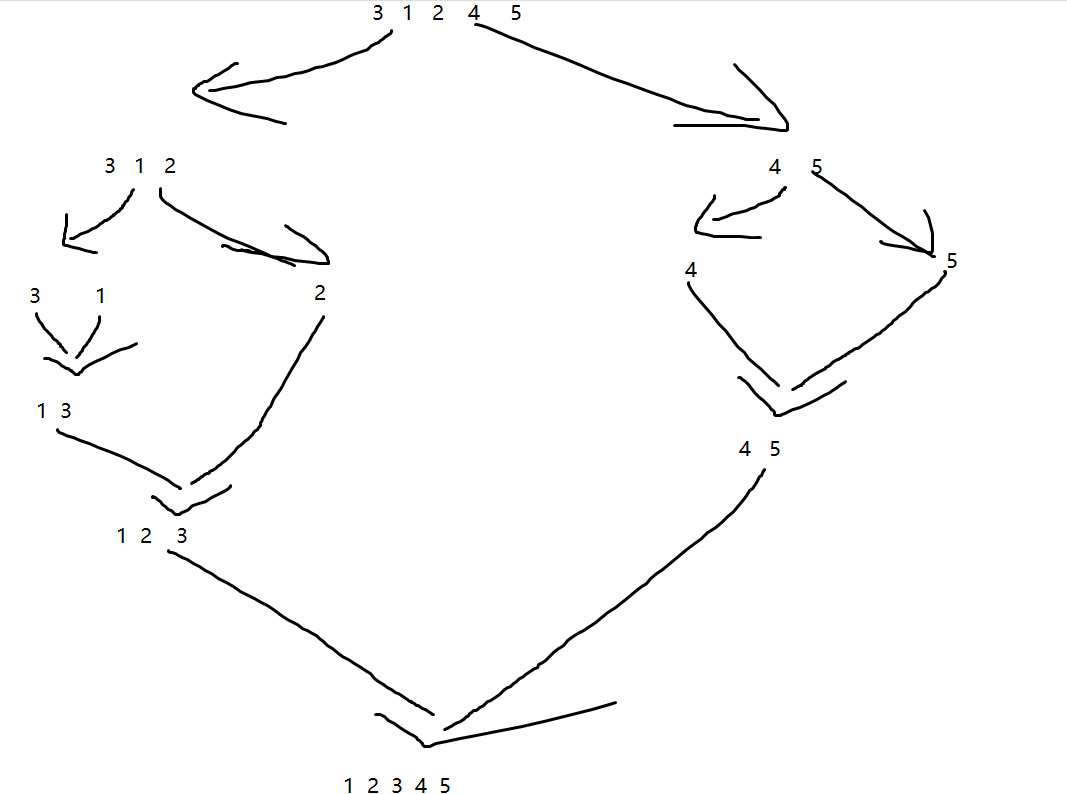
But what is the relationship between sorting and reverse order on quantity?
We will find that when we merge arrays, if the number of left intervals has not been merged, the number of right intervals will be merged. At this time, the remaining unconsolidated numbers in the left interval (the number of numbers is mid-i+1) are greater than this number, then we can find the number in reverse order in the process of recursive sorting.

#include<iostream>
using namespace std;
const int N=1e5+10;
int n;
int arr[N],tmp[N];
unsigned long long ans=0;
void merge_sort(int l, int r){
    if(l>=r)    return ;
    int mid=l+r>>1;
    merge_sort(l,mid);
    merge_sort(mid+1,r);
    int i=l,j=mid+1,s=0;
    while(i<=mid&&j<=r){
        if(arr[i]<=arr[j])   tmp[s++]=arr[i++];
        else {
            tmp[s++]=arr[j++];
            ans+=mid-i+1;
        }
    }
    while(i<=mid) tmp[s++]=arr[i++];
    while(j<=r) tmp[s++]=arr[j++];
    for(int i=l;i<=r;i++){
        arr[i]=tmp[i-l];
    }
}
int main(){
    ios::sync_with_stdio(false);
    cin.tie(0);
    cout.tie(0);
    cin>>n;
    for(int i=0;i<n;i++){
        cin>>arr[i];
    }
    merge_sort(0,n-1);
    cout<<ans;
    return 0;
}

Bucket sorting

You have learned two algorithms. You may ask, why learn bucket sorting? In fact, it is also the reason for the application scenario.

Bucket sorting is an extended version of counting sorting. Counting sorting can be regarded as that each bucket only stores the same elements, while bucket sorting each bucket stores a certain range of elements. Through the mapping function, map the elements in the array to be sorted to each corresponding bucket, sort the elements in each bucket, and finally put the elements in the non empty bucket into the original sequence one by one.
Bucket sorting needs to ensure that the elements are evenly dispersed as far as possible, otherwise when all data are concentrated in the same bucket, bucket sorting will be invalid.

Here is a typical example of bucket sorting:

In this problem, the prefix and are used in the processing of the haystack. We will talk about this later. Now we only need to focus on the sorting part later. Because K < = 25000, the data range of the haystack height is small, so we can open up an array of 25001 size, in which b[i] represents the number of haystacks with height I. such time complexity is O(n) level, See the code in detail

#include<bits/stdc++. h> / / Universal header file
using namespace std;
int s[1000010],b[25010];
int main(){
    int n,m;
    cin>>n>>m;
    for(int i = 1;i<=m;++i){
        int a,b;
        cin>>a>>b;
        s[a]++;
        s[b+1]--;
    }
    for(int i = 1;i<=n;++i)s[i]+=s[i-1];//Prefix and processing can be ignored, just know that the height of the ith haystack is stored in the final s[i]
    for(int i = 1;i<=n;++i)b[s[i]]++;  //s[i]<=25000
    int k = (n+1)/2;//middle
    for(int i = 0;i<=25000;++i){
        k-=b[i];
        if(k<=0){
            cout<<i;
            return 0;
        }
    }
    return 0;
}

In this way, bucket sorting also has its wonderful use.

Summary: various sorting methods have their own characteristics. We should be familiar with their characteristics in order to find an appropriate solution when doing problems!

That's all for the blog in this section. The preview of the next section: binary search and binary answer