Take a[5] as an example
a[5] = {9,6,15,4,2};
1. Simple Selection Sorting
Traversing through the array finds the minimum (or maximum) value of the array and places it at position 0. Then scratch off position 0, traverse through the remaining numbers to find the best value, and put it on position 1 of the array, and so on
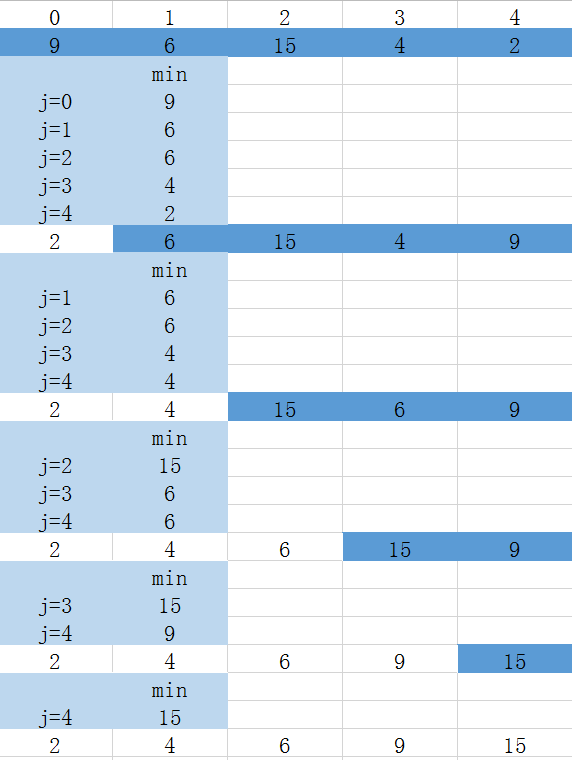
Selecting the smallest record from i records requires comparing i-1 times
I(i=0~n-2) Trip Selecting the smallest record from n-i records requires comparing n-i-1 times
Simple selection sort for n records, number of comparisons: n*(n-1)/2
Number of moves, positive order minimum 0, reverse order maximum 3(n-1)
Simple selection ranks best, with O(n^2) for worst and average time complexity
The time complexity of a simple selection sort is independent of the order of the initial sequence
The code snippet is as follows
for(i=0;i<5;i++){
min = a[i];
k_min = i;
for(j=i+1;j<5;j++){
if(min>a[j]){
min = a[j];
k_min = j;
}
}
if(k_min != i){
a[k_min] = a[i];
a[i] = min;
}
}
2. Sorting by bubble method
The name of this algorithm comes from the fact that the larger (or smallest) elements float slowly to the top of the series (ascending or descending) by exchange, just as the bubbles of carbon dioxide in carbonated drinks eventually float to the top, hence the name Bubble Sort.
Select a direction to scan, comparing the values of the two adjacent elements of the array one by one, placing smaller numbers (sorted from smallest to largest) before larger ones
The illustration is as follows
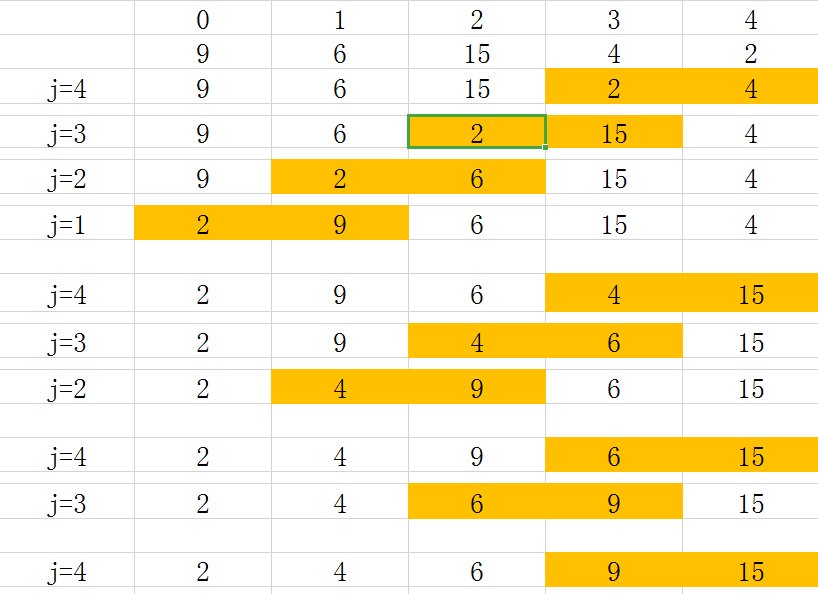
Best case - the keywords are ordered in the record sequence:
Only one bubble is needed
Number of comparisons = n-1
Number of moves = 0;
Worst case - keywords are in reverse order in the record sequence:
n-1 bubbles are required
Number of comparisons = n(n-1)/2
Move times = 3n*(n-1)/2
So the best time complexity for bubble sorting is O(n) and the worst time complexity is O(n^2);
The improved bubble sort code snippet is as follows
for( int i = 1; i < size; i++ ){ //Outer loop 1~size-1
bool exchange = false;
for( int j = size - 1; j >= i; j-- ){ //Inner loop i~size-1
if( a[j] < a[j-1] ){
exchange = true; //If no keywords are exchanged after a bubble, the sequence is arranged
swaq( a[j], a[j-1] ); //Swap Two Numbers
}
}
if( exchange == false ){
break;
}
}
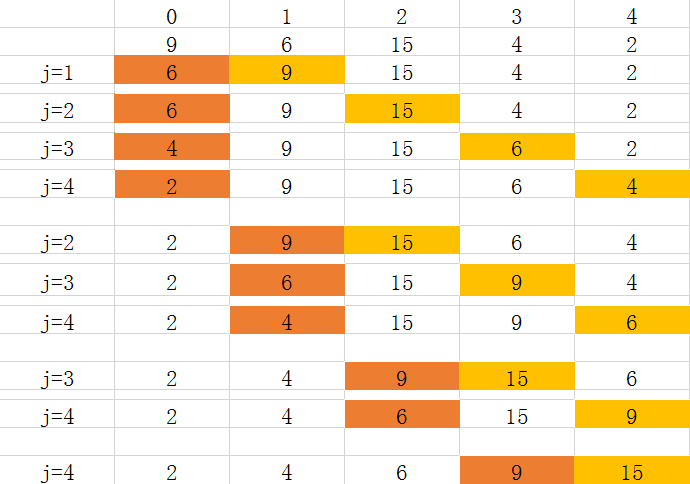
3. Exchange Sorting
The difference between bubble sort and bubble sort is that
Bubble sorting is a process of comparing edges and moving edges, comparing adjacent elements one by one. Exchange ordering is to select a location and compare relative sizes one by one and exchange with fixed locations
The illustration is as follows
The code snippet is as follows:
for(i=0;i<size;i++){
for(j=i+1;j<size;j++){
if(a[j]>a[j-1]){
swap(a[j],a[j-1]);
}
}
}
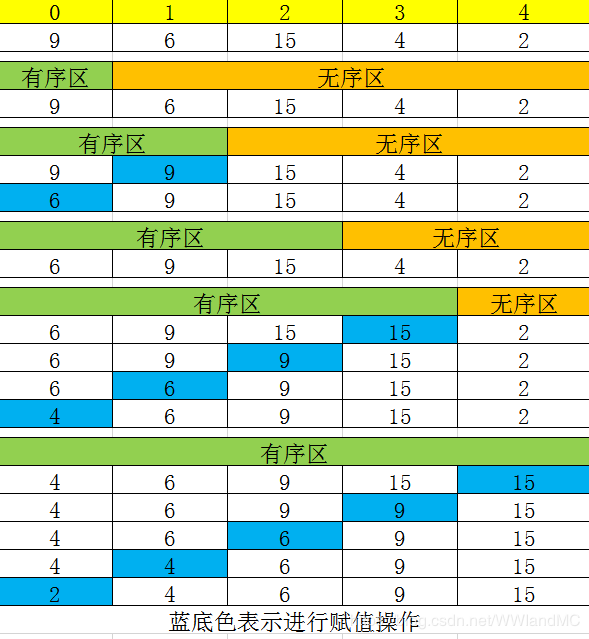
4. Direct insert sorting
The basic idea is to divide the initial sequence into ordered and disordered regions, and insert the elements of the disordered regions into ordered regions one by one until the ordered regions contain all the data. Note that ordered areas are not necessarily ordered. Initially, an ordered region has only one element (only one element can be considered ordered), and it contains an unordered region n-1 Elements are inserted into an ordered area.
for(i=1;i<size;i++){
if(a[i]<a[i-1]){ //Enter the sorting process only if the order is reversed
tmp = a[i];
j = i-1;
do{ //Find the insertion location of a[i]
a[j+1] = a[j]; //Move records with keywords greater than a[i] backwards
j--;
}while((j>=0) && (a[j]>tmp));
a[j+1] = tmp; //Insert in j+1
}
}
In the best case - keywords are positively ordered in the record sequence
Number of comparisons = n-1; Number of element moves = 0;
In the best case, the time complexity is O(n)
Worst case - keywords are in reverse order in the record sequence
Number of comparisons = n(n-1)/2; Number of element moves = (n-1)(n+4)/2;
Worst case time complexity is O(n^2)
Average time complexity is O(n^2)
Sort and find <stdlib. H>
qsort
void qsort( void *base, size_t n_elements, size_t el_size, int ( *compare )( void const *, void const * ) ) ;
The last parameter is a function pointer
bsearch
void bsearch( void const *key, void const *base, size_t n_elements, size_t el_size, int ( *compare )( void const *, void const * ) );
bsearch works by dichotomizing and arrays need to be pre-sorted
#include <stdio.h>
#include <stdlib.h>
int
compare( void const *a, void const *b )
{
return ( *( int* )a ) > ( *( int* )b ) ? 1 : 0;
}
int
main( int argc, char *argv[] )
{
int i;
int key = 110;
int *ans;
int a[] = { 0, 110, 222, 55 };
qsort( a, sizeof(a) / sizeof( int ), sizeof( int ), compare );
for( i = 0; i < sizeof( a ) / sizeof( int ); i++ ){
printf("%d ", a[i]);
}
ans = ( int* )bsearch( &key, a, sizeof( a ) / sizeof( int ), sizeof( int ), compare );
if( ans != NULL ){
printf("\n%d", *ans);
}else{
printf("\nNot Found");
}
return 0;
}