LRU caching mechanism

1. Title

Original question link
Using the data structure you have mastered, design and implement an LRU (least recently used) caching mechanism. It should support the following operations: get data and write data put.

• Get data (key) - if the keyword (key) exists in the cache, get the value of the keyword (always positive), otherwise return - 1.
• Write data put(key, value) - if the keyword already exists, change its data value; If the keyword does not exist, insert the group keyword / value. When the cache capacity reaches the maximum, it should delete the longest unused data value before writing new data, so as to make room for new data values.
• Can you complete these two operations within O(1) time complexity?

Example:

/* The cache capacity is 2 */
LRUCache cache = new LRUCache(2);
// You can think of cache as a queue
// Suppose the left is the head of the team and the right is the tail
// The most recently used ones are at the head of the queue, and those that have not been used for a long time are at the end of the queue
// Parentheses indicate key value pairs (key, val)

cache.put(1, 1);
// cache = [(1, 1)]
cache.put(2, 2);
// cache = [(2, 2), (1, 1)]
cache.get(1);       // Return 1
// cache = [(1, 1), (2, 2)]
// Explanation: because key 1 was accessed recently, it was advanced to the head of the team
// Returns the value 1 corresponding to key 1
cache.put(3, 3);
// cache = [(3, 3), (1, 1)]
// Explanation: the cache capacity is full. You need to delete the content to free up the location
// Priority is given to deleting data that has not been used for a long time, that is, data at the end of the queue
// Then insert the new data into the team head
cache.get(2);       // Return - 1 (not found)
// cache = [(3, 3), (1, 1)]
// Explanation: there is no data with key 2 in the cache
cache.put(1, 4);    
// cache = [(1, 4), (3, 3)]
// Explanation: key 1 already exists. Overwrite the original value 1 with 4
// Don't forget to advance key value pairs to the head of the team

2. Train of thought

What is LRU algorithm: it is a cache elimination strategy.

• The computer's cache capacity is limited. If the cache is full, delete some content and make room for new content. But the question is, what should be deleted? We certainly want to delete useless caches and keep useful data in the cache for future use. So, what kind of data do we judge as "useful"?
• LRU cache elimination algorithm is a common strategy. The full name of LRU is Least Recently Used, that is, we think the recently used data should be "useful", and the data that has not been used for a long time should be useless. When the memory is full, priority will be given to deleting the data that has not been used for a long time.

The LRU algorithm actually allows you to design data structures:

• First, receive a capacity parameter as the maximum cache capacity, and then implement two API s,
• One is to store key value pairs in the put(key, val) method,
• The other is the get(key) method to get the val corresponding to the key. If the key does not exist, it returns - 1.

Note that both get and put methods must have O(1) time complexity

analysis:
Hash table lookup is fast, but the data has no fixed order; The linked list can be divided into order. Insertion and deletion are fast, but search is slow. So combine it to form a new data structure: hash linked list.

• The core data structure of LRU cache algorithm is the combination of hash linked list, bidirectional linked list and hash table. The data structure looks like this:

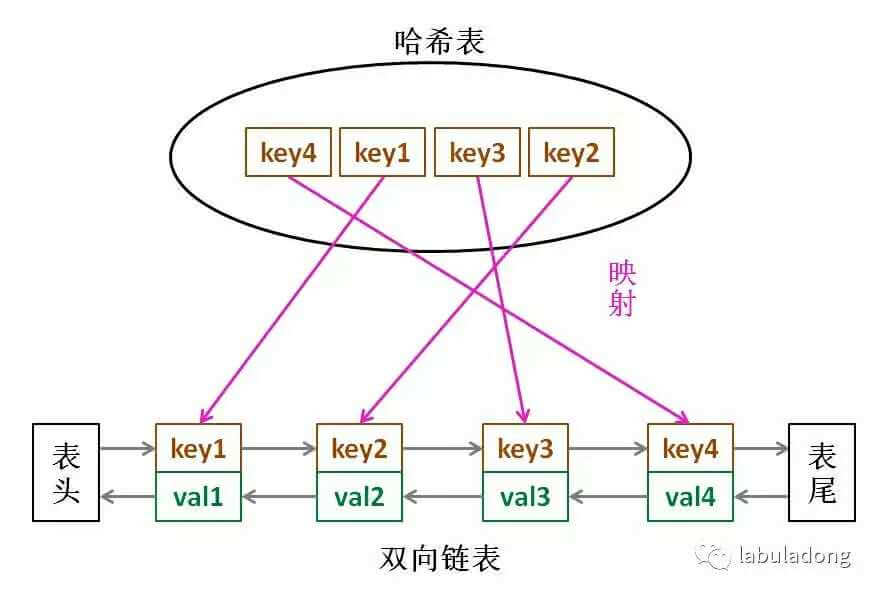
"Why do I have to use a two-way linked list?"

• Because we need to delete. Deleting a node requires not only the pointer of the node itself, but also the pointer of its predecessor node. The two-way linked list can support direct search of precursors and ensure the time complexity of the operation
  O(1).

Since the key has been saved in the hash table, why do you need to save key value pairs in the linked list? Just save the value?

• When the cache capacity is full, we not only delete the last Node, but also delete the key mapped to the Node in the map at the same time, and this key can only be obtained by the Node. If only val is stored in the Node structure, we cannot know what the key is, and we cannot delete the key in the map, resulting in an error.

3. Problem solution

1. get() operation: two cases

• The accessed key does not exist, return -1;
• If the key exists, delete the original position of (key, value) in the cache, change (k, v) to the new position of the team head, and update the position corresponding to the key in the map

  public int get(int key) {
        Node node = cache.get(key);
        if (node == null) {
            return -1;
        }
        // If the key exists, first locate it through the hash table, and then move it to the header
        moveToHead(node);
        return node.value;
    }

1. push (k,v) operation: two cases

• 1. The key already exists in the cache. Delete the original location of (key, value) in the cache, add (k,v) in the header, and update the location corresponding to the key in the map
• 2. If the key does not exist, judge whether the cache is full, which can be divided into two cases
  • When the cache is not full, add (k,v) to the header and update the location corresponding to the key in the map
  • When the cache is full, delete the last element corresponding to the cache in the map, delete the key value pair at the end of the list, add (k,v) to the cache in the header, and update the position corresponding to the key in the map

public void put(int key, int value) {
        Node oldNode = cache.get(key);
        if (oldNode == null) {
            Node newNode = new Node(key, value);
            cache.put(key, newNode);
            addToHead(newNode);
            size++;
            if (size > capacity) {
                Node res = removeTail();
                cache.remove(res.key);
                size--;
            }
        } else {
            oldNode.value = value;
            moveToHead(oldNode);
        }
    }

Based on the above results:

public class LRUCache {
    class DLinkedNode {
        int key;
        int value;
        DLinkedNode prev;
        DLinkedNode next;
        public DLinkedNode() {}
        public DLinkedNode(int _key, int _value) {key = _key; value = _value;}
    }

    private Map<Integer, DLinkedNode> cache = new HashMap<Integer, DLinkedNode>();
    private int size;
    private int capacity;
    private DLinkedNode head, tail;

    public LRUCache(int capacity) {
        this.size = 0;
        this.capacity = capacity;
        // Using pseudo header and pseudo tail nodes
        head = new DLinkedNode();
        tail = new DLinkedNode();
        head.next = tail;
        tail.prev = head;
    }

    public int get(int key) {
        DLinkedNode node = cache.get(key);
        if (node == null) {
            return -1;
        }
        // If the key exists, first locate it through the hash table, and then move it to the header
        moveToHead(node);
        return node.value;
    }

    public void put(int key, int value) {
        DLinkedNode node = cache.get(key);
        if (node == null) {
            // If the key does not exist, create a new node
            DLinkedNode newNode = new DLinkedNode(key, value);
            // Add to hash table
            cache.put(key, newNode);
            // Add to the header of a two-way linked list
            addToHead(newNode);
            ++size;
            if (size > capacity) {
                // If the capacity is exceeded, delete the tail node of the two-way linked list
                DLinkedNode tail = removeTail();
                // Delete the corresponding entry in the hash table
                cache.remove(tail.key);
                --size;
            }
        }
        else {
            // If the key exists, first locate it through the hash table, then modify the value and move it to the header
            node.value = value;
            moveToHead(node);
        }
    }
	//Add node to header
    private void addToHead(DLinkedNode node) {
        node.prev = head;
        node.next = head.next;
        head.next.prev = node;
        head.next = node;
    }
	//Delete any intermediate node
    private void removeNode(DLinkedNode node) {
        node.prev.next = node.next;
        node.next.prev = node.prev;
    }
	//Move node to head
    private void moveToHead(DLinkedNode node) {
        removeNode(node);
        addToHead(node);
    }
	//Delete any node and return it
    private DLinkedNode removeTail() {
        DLinkedNode res = tail.prev;
        removeNode(res);
        return res;
    }
}