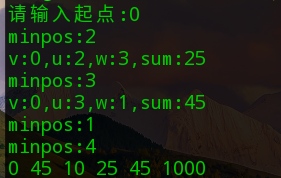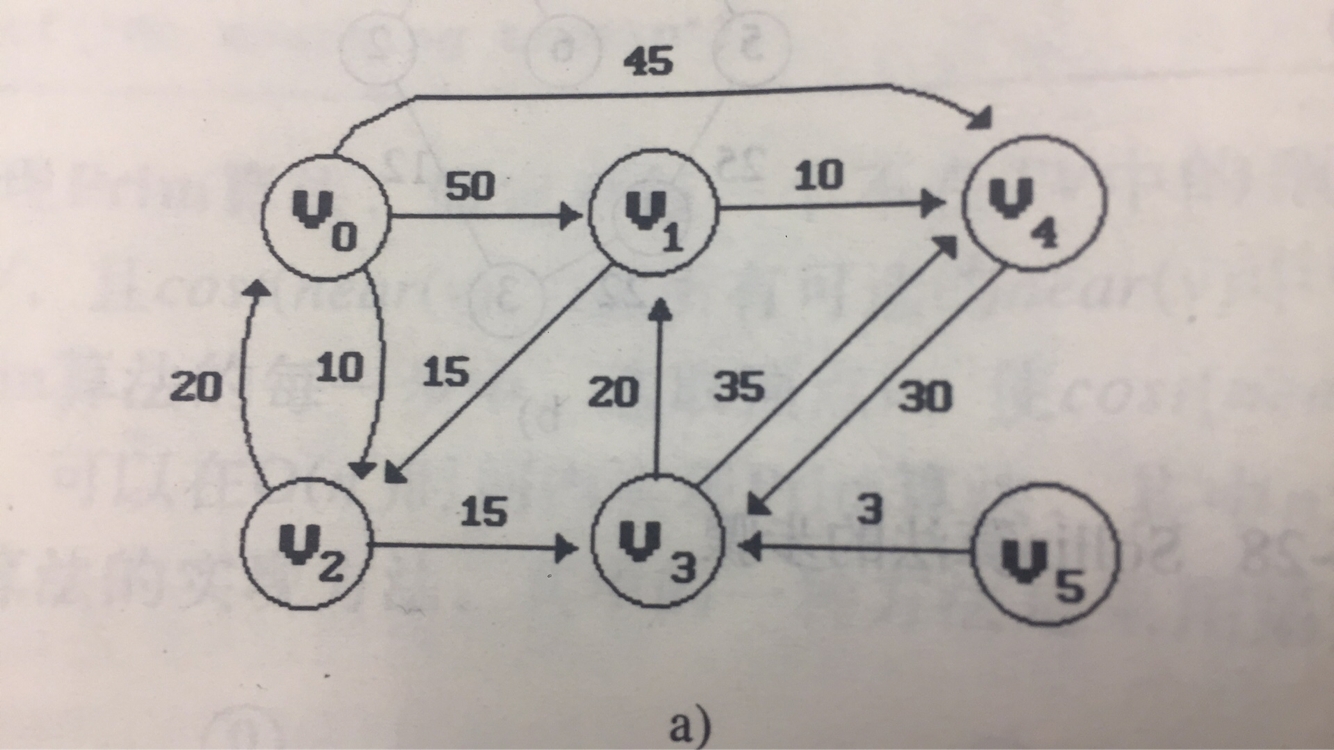
Ideas:
1. Select a point V at will and record the distance from the starting point v to all points with the distance array
(2) Then in the distance array, find the shortest distance from the starting point v to which point, with this point u as the intermediate, find[u]=1, prove that this point already exists in the set, prove that the point has passed
(3) Using the choose function through a loop, you can know which point is the shortest to the starting point and return the index u of that point.
(4) Then start with the point u, and test each of the points w (the point not marked as 1 in the founds array), as long as the distance[u] to a point w (that is, distance[u]+cost[u][w]) is less than the distance[w], modify the distance[w], that is, distance[w] is the minimum distance to the starting point v
#include<stdio.h>
#define MAX 6
int cost[][MAX] =
{
{ 0, 50, 10,1000, 45,1000},
{1000, 0, 15,1000, 10,1000},
{ 20,1000, 0, 15,1000,1000},
{1000, 20,1000, 0, 35,1000},
{1000,1000, 30,1000, 0,1000},
{1000,1000,1000, 3,1000, 0}
};//The corresponding value 1000 of the representation graph proves not connected
int n = MAX;
int found[50] = {0};//Record points that have been made, 0 means no walk
int distance[50] = {0};//Indicates the distance from the starting point to a point
void shortestpath(int v,int cost[][MAX],int distance[],int n,int found[]);
int choose(int distance[],int n,int found[]);//Choose the shortest distance
int main()
{
int v;
printf("Please enter a starting point:");
scanf("%d",&v);
shortestpath(v,cost,distance,n,found);
for(int i=0;i<n;i++)//final result
{
printf("%d ",distance[i]);
}
putchar('\n');
return 0;
}
void shortestpath(int v,int cost[][MAX],int distance[],int n,int found[])
{
int u,w;
for(int i = 0;i < n;i++)//Initialize starting point to all point distances
{
found[i] = 0;
distance[i] = cost[v][i];
}
found[v] = 1;
distance[v] = 0;
for(int i = 0;i < n-2;i++)//Because distance is two plus two at a time, there are only two-2 fewer
{
u = choose(distance,n,found);//Find the minimum distance point, then u becomes an intermediate point
if(u == -1)
continue;
found[u] = 1;//Joined the collection
for(w = 0;w < n;w++)
{
if(!found[w])//distance is not the shortest if you haven't moved past it
{
if(distance[u]+cost[u][w]< distance[w])//If distance[u] plus cost[u][w] is less than distance[w], change the distance[w] value
{
distance[w] = distance[u]+cost[u][w];
}
}
}
}
}
int choose(int distance[],int n,int found[])
{
int min = 9999;
int minpos = -1;
for(int i=0;i < n;i++)
{
if(distance[i] < min && !found[i])
{
min = distance[i];
minpos = i;
}
}
printf("minpos:%d\n",minpos);
return minpos;
}