Vector basic knowledge

slightly

coordinate transformation

Basic concepts of coordinate transformation

I recommend taking a look at his linear algebra series
3blue1brown

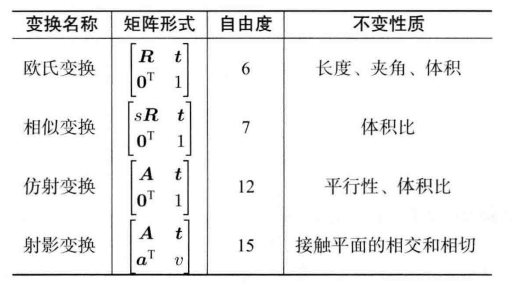
The following formula represents the most basic transformation, Euclidean transformation (only rotation + translation), and R is an orthogonal matrix.
Left multiplying R can make one coordinate (three-dimensional and two-dimensional) rotate to another position. For all points of an object, left multiplying R can make the whole object rotate around the origin.
If you want to produce translation, you have to add a t, a ′ = R a + t a^{'}=Ra+t A '= Ra+t represents a complete Euclidean transformation.
Adding a dimension is a clever mathematical process, which processes the coordinates into ( x , y , z , 1 ) (x,y,z,1) In the form of (x,y,z,1), the rotation and translation can be transformed into matrix multiplication.

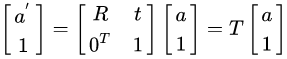
In addition to the basic Euclidean transformation, there are several other changes. The similar transformation is to increase scaling. Affine transformation a is no longer orthogonal (but reversible), and has stretching, but does not change the shape of each face itself. A face, parallelogram or parallelogram. Projective transformation is the imaging method of camera (human eye). If you use 3D modeling software or perspective for painting, you should have a deep understanding.

CODE:

rotate

visualization

Two dimensional rotation

For the two-dimensional, there is only one rotation axis, which is the Z axis (I can experience that the three-dimensional rotation axis is actually in the four-dimensional. You can't imagine the four-dimensional, but you can feel it).
Then the two-dimensional rotation is an angle.

Rotation vector

The rotation matrix R needs the condition that R is orthogonal and there are constraints, that is to say, not all nine variables work. In fact, there are only three degrees of freedom (variables). We use the same rotation direction as a three-dimensional rotation vector. Plus the three degrees of freedom of translation, you can use six degrees of freedom to represent the coordinate transformation.
Rotation vector has singularity. The direct problem of singularity is that it is not differentiable. It's a fart.

3D rotation

The expression of rotation vector is not intuitive enough.
The most intuitive representation of three-dimensional rotation is to use Euler angle. It is easy to understand from the figure below. It is very intuitive to replace a rotation pose by rotating around three axes respectively.
However, it still has singularity. The interpolation between two angles is very difficult, and there are also famous problems Universal lock problem.

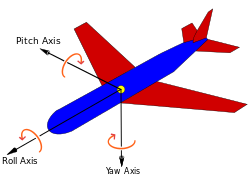
Euler angle transformation

Quaternion

It is very complex and difficult to understand. It can solve the problem of universal lock without singularity. It basically uses quaternion for operation.
Can see this Understand, but it's not very easy to understand.

We can use the unit quaternion (modulo 1) to represent a rotation. Similarly, we can use an imaginary number with modulo 1 to represent a two-dimensional rotation. But this axis of rotation is in four dimensions.

Properties of quaternions

Basic operations own reference books, as long as you know how to represent rotation.

Use of eigen Library

coordinate transformation

#include"ros/ros.h"
#include"iostream"
#include"ctime"
//Eigen core
#include"Eigen/Core"
//Dense matrix operation (inverse, eigenvalue, etc.)
#include"Eigen/Dense"
using namespace std;
using namespace Eigen;

#define MATRIX_SIZE 50

int main(int argc,char** argv)
{
    //Declare a 2 * 3 float matrix
    Matrix<float,2,3> matrix_23;

    //3D vector
    Vector3d v_3d;
    Matrix<float,3,1> vd_3d; //equivalence

    //3x3 matrix
    Matrix3d  matrix_33=Matrix3d::Zero();//Initialize to 0
    //The matrix with uncertain size can be used as dynamic matrix
    Matrix<double,Dynamic,Dynamic> matrix_dynamic;
    //Or simpler
    MatrixXd matrix_x;
    
    //operation

    //input data
    matrix_23<<1,2,3,4,5,6;
    //output
    cout<<"matrix 2x3 is:"<<endl;
    cout<<matrix_23<<endl;

    //Access element
    cout<<"print matrix 2x3:"<<endl;
    for(int i=0;i<matrix_23.rows();i++)
    {
        for(int j=0;j<matrix_23.cols();j++)
        {
            cout<<matrix_23(i,j)<<" ";
        }
        cout<<endl;
    }

    //Matrix and vector multiplication
    v_3d<<3,2,1;
    vd_3d<<4,5,6;
    //The data type does not support implicit conversion
    Matrix<double,2,1> result=matrix_23.cast<double>()*v_3d;
    cout<<"[1,2,3;4,5,6]*[3,2,1]:"<<endl;
    cout<<result.transpose()<<endl;

    //Some matrix operations
    matrix_33=Matrix3d::Random(); //Random number initialization
    matrix_33.transpose(); //Transpose
    matrix_33.sum();//Element and
    matrix_33.trace();//trace
    matrix_33.inverse();//inverse
    matrix_33.determinant();//determinant

    //characteristic value
    //Real symmetry ensures the success of Education
    SelfAdjointEigenSolver<Matrix3d> eigen_solver(matrix_33.transpose()*matrix_33);
    cout<<"eigen matrix is:"<<endl;
    cout<<eigen_solver.eigenvalues()<<endl;
    cout<<"eigen vector is:"<<endl;
    cout<<eigen_solver.eigenvectors()<<endl;

    //solve equations
    //Solving matrix_NN *x=v_Nd equation
    //The amount of direct inversion is the largest
    Matrix<double,MATRIX_SIZE,MATRIX_SIZE> matrix_NN=MatrixXd::Random(MATRIX_SIZE,MATRIX_SIZE);
    matrix_NN=matrix_NN*matrix_NN.transpose();//Guaranteed positive semidefinite
    Matrix<double,MATRIX_SIZE,1> v_Nd = MatrixXd::Random(MATRIX_SIZE,1);
    
    clock_t time_start=clock();//Time keeping
    //Direct inversion
    Matrix<double,MATRIX_SIZE,1> res=matrix_NN.inverse()*v_Nd;
    cout<<"time of normal inverse is:"<<1000*(clock()-time_start)/(double)CLOCKS_PER_SEC<<"ms"<<endl;
    cout<<res.transpose()<<endl;

    //qrd 
    time_start=clock();
    res = matrix_NN.colPivHouseholderQr().solve(v_Nd);
    cout<<"time of Qr is:"<<1000*(clock()-time_start)/(double)CLOCKS_PER_SEC<<"ms"<<endl;
    cout<<res.transpose()<<endl;    

    //For positive definite matrices, cholesky decomposition can be used
    time_start=clock();
    res = matrix_NN.ldlt().solve(v_Nd);
    cout<<"time of cholesky is:"<<1000*(clock()-time_start)/(double)CLOCKS_PER_SEC<<"ms"<<endl;
    cout<<res.transpose()<<endl;        

    //For positive definite matrices, cholesky decomposition can be used
    time_start=clock();
    res = matrix_NN.ldlt().solve(v_Nd);
    cout<<"time of cholesky is:"<<1000*(clock()-time_start)/(double)CLOCKS_PER_SEC<<"ms"<<endl;
    cout<<res.transpose()<<endl;        

    return 0;
}

eigen is written entirely using header files and does not require dynamic link libraries
cmakelist:

cmake_minimum_required(VERSION 3.0.2)
project(eigen_tutorials)

find_package(catkin REQUIRED COMPONENTS
  roscpp
)

find_package(Eigen3 REQUIRED)
###########
## Build ##
###########
include_directories(
# include
  ${catkin_INCLUDE_DIRS}
  ${EIGEN3_INCLUDE_DIRS}
)

add_executable(basic_trans src/basic_trans.cpp)

Geometric module

Basic operation:

#include"ros/ros.h"
#include"iostream"
#include"ctime"
//Eigen core
#include"Eigen/Core"
//Geometric module
#include"Eigen/Geometry"
using namespace std;
using namespace Eigen;

int main(int argc,char** argv)
{
    //Rotation matrix
    Matrix3d rotation_matrix = Matrix3d::Identity();
    //Rotation vector, rotating pi/4 along the z axis
    AngleAxisd rotation_vector(M_PI/4,Vector3d(0,0,1));
    cout.precision(3);//cout accuracy 3
    cout<<"rotation vector:"<<endl;
    // cout<<rotation_ The vector is invalid. It needs to be converted to a rotation matrix
    cout<<rotation_vector.matrix()<<endl;
    //The rotation matrix can be assigned directly
    rotation_matrix=rotation_vector.toRotationMatrix();
    //Coordinate changes can be left multiplied by the rotation matrix or directly by the rotation vector
    Vector3d v(1,0,0);
    //Vector3d v_rotated=rotation_vector*v;
    Vector3d v_rotated=rotation_matrix*v;
    cout<<"after rotation:"<<v_rotated.transpose()<<endl;

    //Euler angle
    Vector3d euler_angles = rotation_matrix.eulerAngles(2,1,0);//zyx order, roll pitch yaw
    cout<<"yaw pitch roll="<<euler_angles.transpose()<<endl;

    //Euclidean transformation, rotation + translation
    Isometry3d T; //4x4 matrix
    T.rotate(rotation_vector); //Assignment using rotation vector
    T.pretranslate(Vector3d(1,3,4)); //Set translation vector
    cout<<"Transform matrix ="<<endl;
    cout<<T.matrix()<<endl;

    //Quaternion
    //You can use the rotation vector assignment, or vice versa
    Quaterniond q=Quaterniond(rotation_vector);
    cout<<"quaternion from roation vector="<<q.coeffs().transpose()<<endl; //(x,y,z,w) the last is the real part 
    //Rotation matrix assignment can also be used
    q=Quaterniond(rotation_matrix);
    //You can use quaternion directly * and it has been overloaded
    v_rotated=q*v; //qvq^{-1}
    //Normal operation
    MatrixXd qv_rotated=(q*Quaterniond(0,1,0,0)*q.inverse()).coeffs(); // (v_rotated,0)
    //Quaterniond tt(0,1,0,0);  The assignment is wxyz, which is opposite to coeffs
    cout<<"after rotation:"<<endl;
    cout<<v_rotated.transpose()<<endl;
    cout<<qv_rotated.transpose()<<endl;
    return 0;
}

example:

Problem Description:
Radish 1 posture q1=[0.35,0.2,0.3,0.1],t1=[0.3,0.1,0.1]
Radish 2 pose q2=[-0.5,0.4,-0.1,0.2],t2=[-0.1,0.5,0.3]
Radish 1 sees a point in its own coordinate system as[0.5,0,0.2]
Find the coordinates of this point in radish 2 coordinate system
*/

#include"ros/ros.h"
#include"iostream"
#include"ctime"
//Eigen core
#include"Eigen/Core"
//Geometric module
#include"Eigen/Geometry"
using namespace std;
using namespace Eigen;
int main(int argc,char **argv)
{
    //First solve the transformation matrix from turnip 1 to the world coordinate system
    Quaterniond q1(0.35,0.2,0.3,0.1);
    q1.normalize();
    Vector3d t1(0.3,0.1,0.1);
    Isometry3d w2one(q1);
    w2one.pretranslate(t1);

    //Then solve the transformation matrix from turnip 2 to the world coordinate system
    Quaterniond q2(-0.5,0.4,-0.1,0.2);
    q2.normalize();
    Vector3d t2(-0.1,0.5,0.3);
    Isometry3d w2two(q2);
    w2two.pretranslate(t2);

    //The transformation matrix is transformed to the world coordinate system first, and then to the 2 coordinate system
    Isometry3d one2two=w2two*w2one.inverse(); //Be careful not to reverse. The latter one is closer to the position, that is, the transformation carried out first
    
    //calculation
    Vector3d res=one2two*Vector3d(0.5,0,0.2);
    cout<<res<<endl;
    return 0;
}