Small ball into blue hole (operator overload)

Title Description

The game of small ball entering the blue hole refers to setting red hole, blue hole and some green triangle blocks in the square array of n*m (n,m value is between 2 and 10), adjusting the green triangle block, making the small ball start from the direction of the red hole hole, reflect through the inclined edge of the triangle block, constantly change the direction of moving forward, and finally enter the blue hole from the direction of the blue hole hole hole. For example: in the initial game layout shown in the left figure below, adjust the triangle block as shown in the right figure, and the ball will enter the blue hole along the blue dotted line.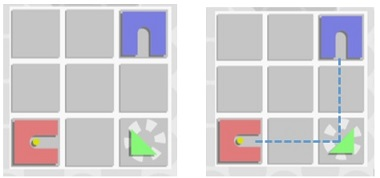

Red hole and blue hole are located in the right, top, left and bottom four directions of the square, respectively represented by the numbers 0, 1, 2 and 3. For example: the red hole opening in the above figure is on the right side of the square, represented by 0. The blue hole is below the square, which is represented by 3.
Click the triangle block to adjust its direction. The order of change is shown in figure (a) - (d) (represented by values 1-4 respectively), and it will continue to cycle in the four directions. For example, click the triangle block in the left figure above three times to change it into the triangle block in the right figure above.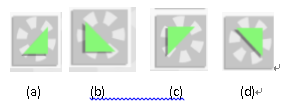

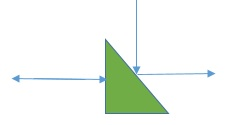
The ball starts from the red hole and moves straight. When it touches the edge of the triangle, it changes its direction. The rules for the ball to change its route are as follows: if the ball touches the right angle edge, it will move in the opposite direction of the original direction, as shown in the straight line on the left of the figure below; if the ball touches the inclined edge, it will change its direction of travel along 90 degrees, as shown in the two straight lines on the right of the figure below (the arrow direction of the straight line can be changed, and it will enter from the horizontal right to move up).

Red hole, blue hole, small ball and triangle block can all be represented by x,y coordinate and direction, defining the base class CPoint class: attribute: x,y,dir (direction), method: public access interface with parameter construction, x,y,dir, overload output, output x,y,dir. Other methods can be added as needed.

Define the chle class: public inheritance CPoint class. Other methods can be added by yourself.

Define triangle block CTriangle class: public inheritance CPoint class. New method: before overloading + +, click the triangle block to adjust the direction of the triangle block according to the sequence (a)-(d) above. Other methods can be added by yourself.

Define CBall class: public inherits cppoint class. New method: heavy load * =, to realize the collision function of small ball and triangle block (change the direction of small ball forward).

Define game class: attribute: square size n, m; color object red hole, blue hole; number of triangle blocks k, triangle block object array (store triangle block data). Methods: constructor, play to realize the game function, set the shape of the triangle block, make the little ball from the red hole to the blue hole. For heavy load output, output the adjusted coordinates and directions of each triangle block according to the input sequence of the triangle block.

The main function is written according to the input and output.

Suppose the coordinates of the upper left corner and the lower right corner of the n*m matrix are (0, 0) and (n-1,m-1).

input

output

sample input

sample output

no solution

2 2 1

0 1 3
1 1 1
0 3 4
4 3 2

Idea: DFS depth first search, backtracking if not satisfied

#include <iostream>
using namespace std;

class CPoint
{
protected:
    int x,y;
    int dir;
public:
    CPoint():x(0),y(0),dir(0){}
    CPoint(int _x,int _y,int _dir):x(_x),y(_y),dir(_dir){}
    int getX(){ return x;}
    int getY(){ return y;}
    int getDir(){ return dir;}
    void setDir(int d){dir=d;}
    friend ostream& operator<<(ostream &out,CPoint &p);
};

ostream &operator<<(ostream &out, CPoint &p) {
    out<<p.x<<" "<<p.y<<" "<<p.dir;
    return out;
}

class CHole:public CPoint
{
public:
    CHole(int x,int y,int dir):CPoint(x,y,dir){}
    friend class CBall;
};

class CTriangle:public CPoint
{
public:
    CTriangle() : CPoint(0, 0, 0) {}
    friend istream& operator>>(istream &in,CTriangle &t);
    friend ostream& operator<<(ostream &out,CTriangle &t);
    void operator++();
    friend class CBall;
};

istream &operator>>(istream &in, CTriangle &t) {
    in>>t.x>>t.y>>t.dir;
    return in;
}

ostream &operator<<(ostream &out, CTriangle &t) {
    out<<t.x<<" "<<t.y<<" "<<t.dir;
    return out;
}

void CTriangle::operator++() {
    //1 is right angle at the bottom right, 2 is right angle at the bottom left, 3 is right angle at the top left, 4 is right angle at the top right
    dir++;
    if(dir>4)
        dir-=4;
}

class CBall:public CPoint
{
public:
    CBall():CPoint(){}
    CBall(int x,int y,int dir):CPoint(x,y,dir){}
    CBall(CHole &h){x=h.x;y=h.y;dir=h.dir;}
    bool toHole(CHole &h);
    bool operator*=(CTriangle &t);
};

bool CBall::operator*=(CTriangle &t)
{
    //0 right, 1 up, 2 left, 3 down
    if(t.dir==1)//Right angle at bottom right
    {
        if(y<t.y && x==t.x && dir==0)//Right up
        {
            dir = 1;
            return true;
        }
        else if(x<t.x && y==t.y && dir==3)//Down to left
        {
            dir = 2;
            return true;
        }
        else if(y>t.y && x==t.x && dir==2)//Left to right
        {
            dir = 0;
            return true;
        }
        else if(x>t.x && y==t.y && dir==1)//Up down
        {
            dir = 3;
            return true;
        }
    }
    //0 right, 1 up, 2 left, 3 down
    else if(t.dir==2)//2 is the right angle at the bottom left
    {
        if(y<t.y && x==t.x && dir==0)//Right to left
        {
            dir = 2;
            return true;
        }
        else if(x<t.x && y==t.y && dir==3)//Down to right
        {
            dir = 0;
            return true;
        }
        else if(y>t.y && x==t.x && dir==2)//Left up
        {
            dir = 1;
            return true;
        }
        else if(x>t.x && y==t.y && dir==1)//Up down
        {
            dir = 3;
            return true;
        }
    }
    //0 right, 1 up, 2 left, 3 down
    else if(t.dir==3)//3 is the right angle on the left
    {
        if(y<t.y && x==t.x && dir==0)//Right to left
        {
            dir = 2;
            return true;
        }
        else if(x<t.x && y==t.y && dir==3)//Down to up
        {
            dir = 1;
            return true;
        }
        else if(y>t.y && x==t.x && dir==2)//Left down
        {
            dir = 3;
            return true;
        }
        else if(x>t.x && y==t.y && dir==1)//Up to right
        {
            dir = 0;
            return true;
        }
    }
    //0 right, 1 up, 2 left, 3 down
    else if(t.dir==4)//4 is right angle on the right
    {
        if(y<t.y && x==t.x && dir==0)//Right down
        {
            dir = 3;
            return true;
        }
        else if(x<t.x && y==t.y && dir==3)//Down to up
        {
            dir = 1;
            return true;
        }
        else if(y>t.y && x==t.x && dir==2)//Left to right
        {
            dir = 0;
            return true;
        }
        else if(x>t.x && y==t.y && dir==1)//Up to left
        {
            dir = 2;
            return true;
        }
    }
    return false;
}

//The ball went into the hole
bool CBall::toHole(CHole &h) {
    //0 right, 1 up, 2 left, 3 down
    if(h.dir==0)//The hole is on the right
    {
        if(y>h.y && x==h.x && dir==2)
            return true;
    }
    else if(h.dir==1)//The hole is above
    {
        if(x<h.x && y==h.y && dir==3)
            return true;
    }
    else if(h.dir==2)//The hole is on the left
    {
        if(y<h.y && x==h.x && dir==0)
            return true;
    }
    else if(h.dir==3)//The hole is below
    {
        if(x>h.x && y==h.y && dir==1)
            return true;
    }
    return false;
}

class CGame
{
private:
    int n,m;
    CHole red,blue;
    int k;
    CTriangle *triangle;
    bool *visit;
public:
    CGame(int _n,int _m,CHole &r,CHole &b,int _k,CTriangle *t);
    ~CGame(){delete []triangle;delete []visit;}
    bool play();
    bool DFS(CBall ball);
    bool isOver();
    friend ostream& operator<<(ostream &out,CGame &g);
};

CGame::CGame(int _n, int _m, CHole &r, CHole &b, int _k, CTriangle *t):n(_n),m(_m),red(r),blue(b),k(_k) {
    triangle = new CTriangle[k];
    for(int i=0;i<k;i++)
        triangle[i]=t[i];
    visit = new bool[k];
    for(int i=0;i<k;i++)
        visit[i]= false;
}

bool CGame::DFS(CBall ball) {
    int flag=4;
    for(int i=0;i<k;i++)
    {
        int beforeDir=ball.getDir();
        if(!visit[i])//Can touch a triangle
        {
            if(ball*=triangle[i])
            {
                visit[i] = true;
                CBall b(triangle[i].getX(),triangle[i].getY(),ball.getDir());
                if(!DFS(b))
                {
                    flag--;
                    ++triangle[i];
                    ball.setDir(beforeDir);
                    visit[i] = false;
                    if(flag!=0)
                        i--;
                    else
                        flag=4;
                }
                else
                    return true;
            }
        }
    }
    return isOver() && ball.toHole(blue);
}

bool CGame::isOver() {
    for(int i=0;i<k;i++)
        if(!visit[i])
            return false;
    return true;
}


bool CGame::play() {
    CBall ball(red);
    return DFS(ball);
}

ostream &operator<<(ostream &out, CGame &g) {
    for(int i=0;i<g.k;i++)
        out<<g.triangle[i]<<endl;
    return out;
}


int main()
{
    int t;
    cin>>t;
    while (t--)
    {
        int n,m,x,y,dir;
        cin>>n>>m;
        cin>>x>>y>>dir;
        CHole red(x,y,dir);
        cin>>x>>y>>dir;
        CHole blue(x,y,dir);
        int k;
        cin>>k;
        CTriangle *triangle=new CTriangle[k];
        for(int i=0;i<k;i++)
            cin>>triangle[i];
        CGame game(n,m,red,blue,k,triangle);
        if(game.play())
            cout<<game;
        else
            cout<<"no solution"<<endl;
        cout<<endl;
        delete []triangle;
    }
    return 0;
}